Organização dos dados

Nesta etapa, iniciamos carregando os dados e pacotes, nesse caso, principalmente o pacote REAT. Neste caso, os dados são dos municípios de Mato Grosso do Sul, de 2002 a 2015. Observar que esse dataset contém dados “ausentes” (missings) e o pesquisador deverá cuidar destes detalhes antes da análise.

Os dados estão organizados por colunas para o valor adicionado bruto (VAB) do setor agropecuário (agro), VAB do setor da administração pública (apu), os impostos (imp), VAB do setor da indústria (ind), VAB do setor de serviços (serv), o VAB total (vabt), o PIB -Produto Interno Bruto- (pib), a população municipal (pop), o PIB per capita (pibpc), o share da população municipal no estado (spop = pop do município/pop do estado), o share do PIB municipal no estado (y = pib do município/pib do estado), e a produtividade relativa (R=y/spop).

Os dados foram organizados previamente a partir de dados das contas regionais municipais do IBGE (2020a) (Instituto Brasileiro de Geografia e Estatística) (Tabela 5938 - Produto Interno Bruto dos Municípios) e da informação da população estimada (Tabela 6579) para informação ao TCU (Tribunal de Contas da União) pelo IBGE (2020b). Em virtude das desagregações municipais, os municípios de Figueirão e Paraíso das Águas foram excluídos da análise (sabemos que tal procedimento tem limitações mas em se tratando de um exercício ilustrativo do método, não gerará maiores implicações). Portanto, os dados sem os missings estão na planilha dados2.

library(REAT)
library(readxl)
# help('REAT')
dados <- read_excel("dadospib_popms.xlsx", sheet = "dados")
# DT::datatable(dados)

# excluindo as observacoes de Figueirao e Paraiso das Aguas
dados2 <- read_excel("dadospib_popms.xlsx", sheet = "dados2")

Separaremos as variáveis a saber: pib, pop, pibpc, R.

pib <- dados2[87:100]
pop <- dados2[101:114]
pibpc <- dados2[115:128]
R <- dados2[157:170]

Estatísticas descritivas das séries de PIB per capita e população.

summary(pibpc)

   pibpc2002       pibpc2003       pibpc2004        pibpc2005     
 Min.   : 2684   Min.   : 3227   Min.   :  3096   Min.   :  3580  
 1st Qu.: 4674   1st Qu.: 6540   1st Qu.:  6689   1st Qu.:  6536  
 Median : 6061   Median : 7977   Median :  8296   Median :  8377  
 Mean   : 8159   Mean   :11222   Mean   : 11769   Mean   : 11436  
 3rd Qu.: 8867   3rd Qu.:12046   3rd Qu.: 12039   3rd Qu.: 11619  
 Max.   :66252   Max.   :83192   Max.   :117442   Max.   :128890  
   pibpc2006        pibpc2007       pibpc2008        pibpc2009     
 Min.   :  3744   Min.   : 4427   Min.   :  5084   Min.   :  5251  
 1st Qu.:  7210   1st Qu.: 8264   1st Qu.:  9638   1st Qu.: 10469  
 Median :  9471   Median :10680   Median : 12656   Median : 13661  
 Mean   : 12096   Mean   :13160   Mean   : 15877   Mean   : 16801  
 3rd Qu.: 13372   3rd Qu.:14265   3rd Qu.: 16697   3rd Qu.: 17168  
 Max.   :113228   Max.   :96066   Max.   :135707   Max.   :142556  
   pibpc2010        pibpc2011        pibpc2012        pibpc2013     
 Min.   :  5806   Min.   :  6420   Min.   :  7141   Min.   :  9061  
 1st Qu.: 11675   1st Qu.: 13229   1st Qu.: 14637   1st Qu.: 15072  
 Median : 15522   Median : 17862   Median : 19065   Median : 21462  
 Mean   : 19933   Mean   : 22321   Mean   : 24673   Mean   : 27171  
 3rd Qu.: 20674   3rd Qu.: 23541   3rd Qu.: 25755   3rd Qu.: 27352  
 Max.   :234013   Max.   :212794   Max.   :215305   Max.   :259532  
   pibpc2014        pibpc2015     
 Min.   :  9627   Min.   :  9604  
 1st Qu.: 17162   1st Qu.: 18699  
 Median : 23950   Median : 25860  
 Mean   : 30152   Mean   : 31838  
 3rd Qu.: 31463   3rd Qu.: 33713  
 Max.   :289319   Max.   :246333  

summary(pop)

    pop2002          pop2003          pop2004          pop2005      
 Min.   :  3165   Min.   :  2926   Min.   :  2426   Min.   :  2148  
 1st Qu.:  8053   1st Qu.:  8052   1st Qu.:  8050   1st Qu.:  8049  
 Median : 12923   Median : 13180   Median : 13426   Median : 13634  
 Mean   : 27800   Mean   : 28178   Mean   : 28932   Mean   : 29371  
 3rd Qu.: 20488   3rd Qu.: 20675   3rd Qu.: 20519   3rd Qu.: 20426  
 Max.   :692549   Max.   :705975   Max.   :734164   Max.   :749768  
    pop2006          pop2007          pop2008          pop2009      
 Min.   :  1873   Min.   :  3117   Min.   :  3198   Min.   :  3165  
 1st Qu.:  7979   1st Qu.:  8168   1st Qu.:  8401   1st Qu.:  8397  
 Median : 13698   Median : 13979   Median : 14416   Median : 14569  
 Mean   : 29806   Mean   : 29377   Mean   : 30294   Mean   : 30611  
 3rd Qu.: 20789   3rd Qu.: 20916   3rd Qu.: 21546   3rd Qu.: 21677  
 Max.   :765247   Max.   :724524   Max.   :747190   Max.   :755107  
    pop2010          pop2011          pop2012          pop2013      
 Min.   :  3518   Min.   :  3520   Min.   :  3522   Min.   :  3570  
 1st Qu.:  7985   1st Qu.:  7956   1st Qu.:  7972   1st Qu.:  8288  
 Median : 14833   Median : 14972   Median : 15065   Median : 15429  
 Mean   : 31768   Mean   : 32138   Mean   : 32434   Mean   : 33498  
 3rd Qu.: 22341   3rd Qu.: 22621   3rd Qu.: 23016   3rd Qu.: 23888  
 Max.   :786797   Max.   :796252   Max.   :805397   Max.   :832352  
    pop2014          pop2015      
 Min.   :  3570   Min.   :  3570  
 1st Qu.:  8429   1st Qu.:  8567  
 Median : 15534   Median : 15637  
 Mean   : 33917   Mean   : 34326  
 3rd Qu.: 24078   3rd Qu.: 24414  
 Max.   :843120   Max.   :853622  

Na próxima seção, faremos os indicadores de análise.

Coeficiente de variação (\(CV\))

O \(CV\) permite resumir as disparidades regionais (ex: no PIB regional per capita) em um indicador. Neste caso, o \(CV\) não está ponderado pela população e pode ser padronizado para ficar entre 0 e 1.

No exemplo a seguir, não está padronizado. Veja a fórmula para cálculo do CV.

\[ CV = \frac{{\sqrt {\left( {\frac{1}{{T - 1}}} \right){{\sum\limits_i {\left( {{y_i} - \mu } \right)} }^2}} }}{\mu } \]

Na fórmula de \(CV\), para a variável em análise, neste exemplo, \(y_i\) é o PIB per capita do município \(i\); \(\mu\) é o PIB per capita do estado; e, T é o número de municípios analisados. Portanto, o coeficiente de variação \(CV\) é o quociente do desvio padrão dividido pela média, e servirá para analisar as disparidades na variável de análise, neste caso, o PIB per capita municipal.

O coeficiente de variação, \(CV\), é uma medida estatística de dispersão, baseada na variância e no desvio-padrão. Desta forma, na análise regional, dá uma ideia de convergência absoluta (ou σ-convergência) em casos de pequena variação no tempo ou no espaço. A redução da dispersão pode ser oriunda de crescimento mais acelerado das localidades mais pobres relativamente àquelas mais ricas, conforme as teorias de convergência de renda.

A expressão tradicional trata o dataset como uma amostra, e por este motivo o denominador da variância é T-1. Se for o universo, então pode-se especificar is.sample = FALSE e a rotina de cv tratará a informação com o denominador igual a T na variância.

attach(pibpc)
# calculo para o PIB per capita para um ano
CVMS.2015 <- cv(pibpc2015, is.sample = FALSE, coefnorm = FALSE, weighting = NULL, 
    wmean = FALSE, na.rm = FALSE)
cat("CVMS.2015 = ", CVMS.2015)

CVMS.2015 =  0.8847709

# Calculo para o PIB per capita de 2002-2015 e plot
cvs.pibpc <- apply(pibpc, MARGIN = 2, FUN = cv)
cat("máximo de cvs.pibpc = ", max(cvs.pibpc))

máximo de cvs.pibpc =  1.290541

# [1] 1.290541
cat("mínimo de cvs.pibpc = ", min(cvs.pibpc))

mínimo de cvs.pibpc =  0.840226

# [1] 0.840226 Calculo do cv para 2002-2015
anos <- 2002:2015

# Plot cv no tempo
plot(anos, cvs.pibpc, "l", ylim = c(0.84, 1.3), xlab = "Ano", ylab = "CV do PIB per capita", 
    main = "CV dos PIB per capita municipais de MS, 2002-2015")

# Calculo de CV normalizado para o PIB per capita de 2002-2015 e plot
cvsn.pibpc <- apply(pibpc, MARGIN = 2, FUN = cv, coefnorm = TRUE)
max(cvsn.pibpc)  # [1] 0.1480351

[1] 0.1480351

min(cvsn.pibpc)  # [1] 0.09638054

[1] 0.09638054

anos <- 2002:2015

# Plot cv no tempo
plot(anos, cvsn.pibpc, "l", ylim = c(0.09, 0.15), xlab = "Ano", ylab = "CV do PIB", 
    main = "CV normalizado dos PIBs per capita municipais de MS, 2002-2015")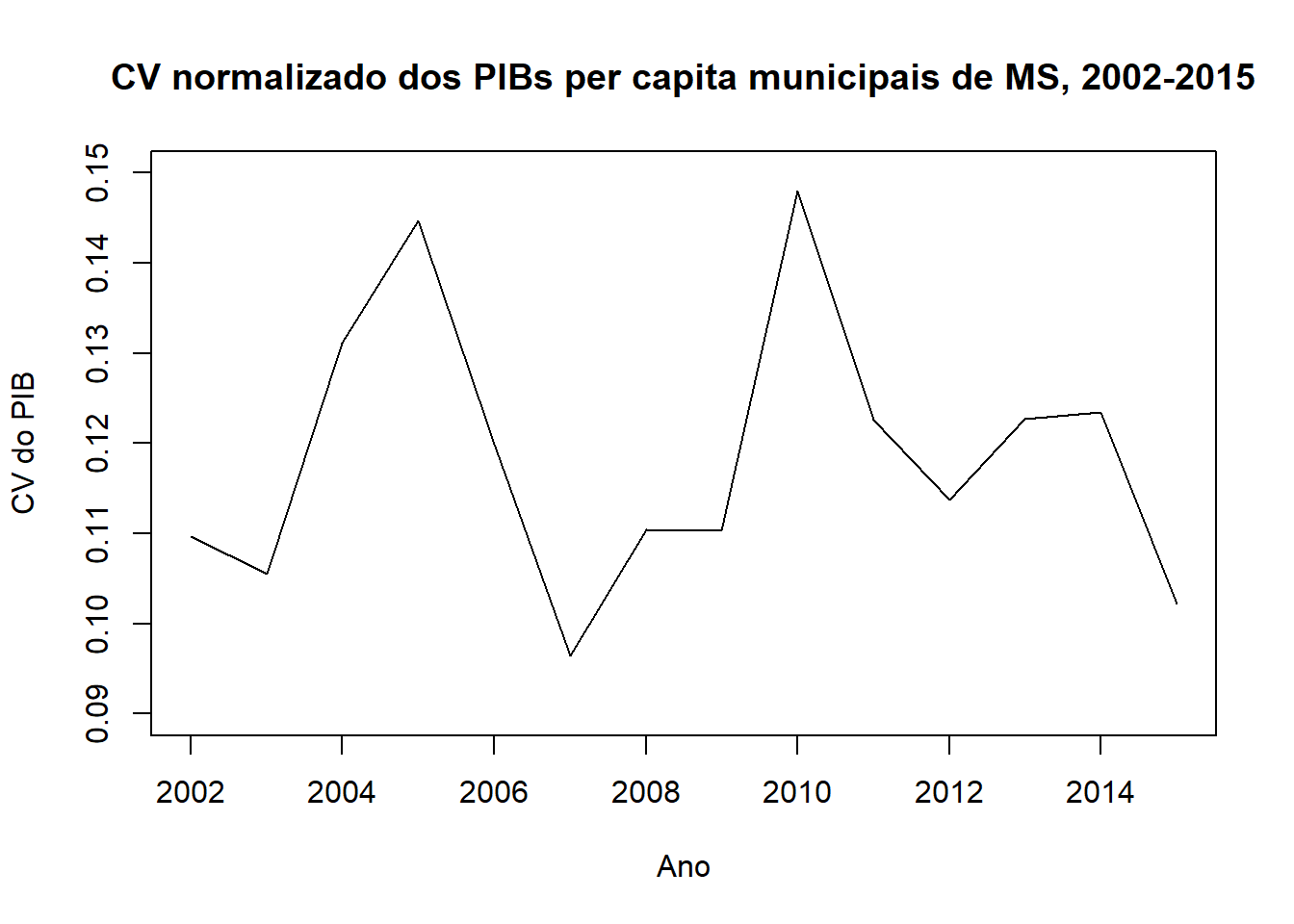

resultado.cv <- as.data.frame(cbind(anos, cvs.pibpc, cvsn.pibpc))
knitr::kable(resultado.cv, caption = "CV e CV normalizado dos PIBs per capita municipais de MS, 2002-2015")

Índice de Williamson (\(V_w\))

Williamson’s population-weighted coefficient of variation

O índice \(V_w\) é um coeficiente de variação ponderado pela parcela da população em cada região. Para a equação de Williamson (1965), para a população \(p_i\) da região \(i\) e população do estado \(N\). O valor de \(V_w\) será 0 (zero) para não existência de desigualdades do PIB per capita (\(y_i\)). A ponderação pela população faz com que o indicador fique melhor que o \(CV\) quando houver regiões com pequenas populações junto a outras de grandes populações. A fórmula é como abaixo:

\[ Vw = \frac{{\sqrt {{{\sum\limits_i {\left( {{y_i} - \mu } \right)} }^2}\left( {\frac{p_i}{{N}}} \right)} }}{\mu } \]

Similarmente ao CV, primeiro calculou-se o Vw para um ano e sem normalizar, depois para os vários anos e com normalização. O comando é o mesmo do CV (cv), do pacote REAT, mas especificando a ponderação em weighting = pop.

# para um ano específico, 2002, para a variável pibpc:
attach(pibpc)
attach(pop)
VwMS.2002 <- cv(pibpc2002, coefnorm = FALSE, weighting = pop2002, wmean = FALSE, 
    na.rm = FALSE)
VwMS.2002

[1] 0.5933009

# para um ano específico, 2015, para a variável pibpc:
VwMS.2015 <- cv(pibpc2015, coefnorm = FALSE, weighting = pop2015, wmean = FALSE, 
    na.rm = FALSE)
VwMS.2015

[1] 0.5262813

# Agora para os vários anos, não padronizando e peso pop farei um a um
Vw.ms <- data.frame(matrix(0, nrow = length(pibpc), ncol = 1))
Vw <- cv(pibpc2002, coefnorm = FALSE, weighting = pop2002)
Vw.ms[1, 1] <- Vw
Vw <- cv(pibpc2003, coefnorm = FALSE, weighting = pop2003)
Vw.ms[2, 1] <- Vw
Vw <- cv(pibpc2004, coefnorm = FALSE, weighting = pop2004)
Vw.ms[3, 1] <- Vw
Vw <- cv(pibpc2005, coefnorm = FALSE, weighting = pop2005)
Vw.ms[4, 1] <- Vw
Vw <- cv(pibpc2006, coefnorm = FALSE, weighting = pop2006)
Vw.ms[5, 1] <- Vw
Vw <- cv(pibpc2007, coefnorm = FALSE, weighting = pop2007)
Vw.ms[6, 1] <- Vw
Vw <- cv(pibpc2008, coefnorm = FALSE, weighting = pop2008)
Vw.ms[7, 1] <- Vw
Vw <- cv(pibpc2009, coefnorm = FALSE, weighting = pop2009)
Vw.ms[8, 1] <- Vw
Vw <- cv(pibpc2010, coefnorm = FALSE, weighting = pop2010)
Vw.ms[9, 1] <- Vw
Vw <- cv(pibpc2011, coefnorm = FALSE, weighting = pop2011)
Vw.ms[10, 1] <- Vw
Vw <- cv(pibpc2012, coefnorm = FALSE, weighting = pop2012)
Vw.ms[11, 1] <- Vw
Vw <- cv(pibpc2013, coefnorm = FALSE, weighting = pop2013)
Vw.ms[12, 1] <- Vw
Vw <- cv(pibpc2014, coefnorm = FALSE, weighting = pop2014)
Vw.ms[13, 1] <- Vw
Vw <- cv(pibpc2015, coefnorm = FALSE, weighting = pop2015)
Vw.ms[14, 1] <- Vw

anos <- 2002:2015

# Plot Vw no tempo
plot(anos, Vw.ms[, 1], "l", xlab = "Ano", ylab = "Vw do PIB per capita", main = "Vw dos PIBs municipais per capita de MS, 2002-2015")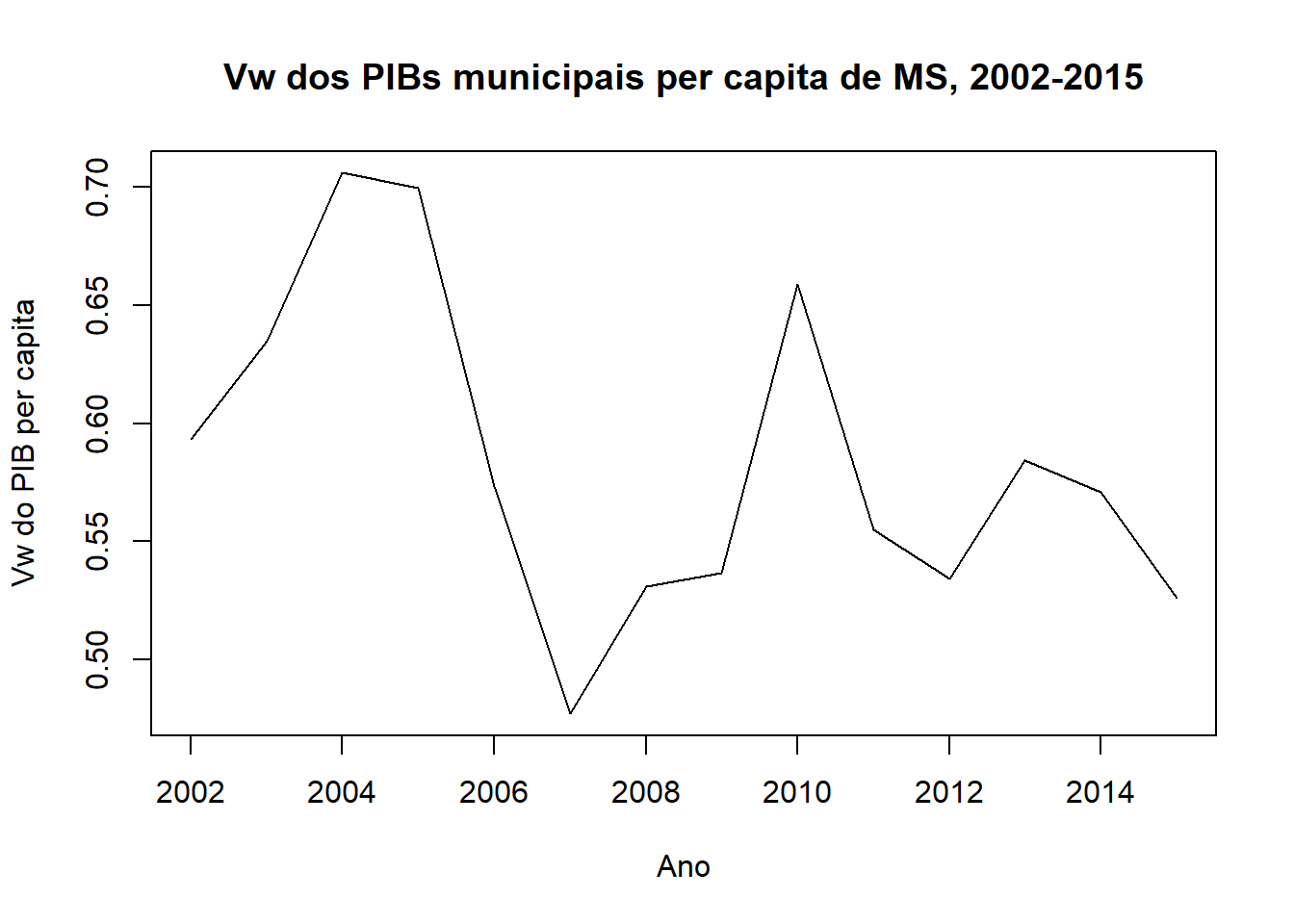

resultado.vw <- as.data.frame(Vw.ms)
rownames(resultado.vw) <- anos
colnames(resultado.vw) <- c("Vw")
knitr::kable(resultado.vw, caption = "Vw dos PIBs per capita municipais de MS, 2002-2015")

Os valores normalizados devem estar entre 0 e 1. Assim, farei a normalização, calculando agora para os vários anos, padronizando e usando o peso (weighting = pop). Farei ano a ano.

Vwn.ms <- data.frame(matrix(0, nrow = length(pibpc), ncol = 1))
Vwn <- cv(pibpc2002, coefnorm = TRUE, weighting = pop2002, wmean = TRUE)
Vwn.ms[1, 1] <- Vwn
Vwn <- cv(pibpc2003, coefnorm = TRUE, weighting = pop2003, wmean = TRUE)
Vwn.ms[2, 1] <- Vwn
Vwn <- cv(pibpc2004, coefnorm = TRUE, weighting = pop2004, wmean = TRUE)
Vwn.ms[3, 1] <- Vwn
Vwn <- cv(pibpc2005, coefnorm = TRUE, weighting = pop2005, wmean = TRUE)
Vwn.ms[4, 1] <- Vwn
Vwn <- cv(pibpc2006, coefnorm = TRUE, weighting = pop2006, wmean = TRUE)
Vwn.ms[5, 1] <- Vwn
Vwn <- cv(pibpc2007, coefnorm = TRUE, weighting = pop2007, wmean = TRUE)
Vwn.ms[6, 1] <- Vwn
Vwn <- cv(pibpc2008, coefnorm = TRUE, weighting = pop2008, wmean = TRUE)
Vwn.ms[7, 1] <- Vwn
Vwn <- cv(pibpc2009, coefnorm = TRUE, weighting = pop2009, wmean = TRUE)
Vwn.ms[8, 1] <- Vwn
Vwn <- cv(pibpc2010, coefnorm = TRUE, weighting = pop2010, wmean = TRUE)
Vwn.ms[9, 1] <- Vwn
Vwn <- cv(pibpc2011, coefnorm = TRUE, weighting = pop2011, wmean = TRUE)
Vwn.ms[10, 1] <- Vwn
Vwn <- cv(pibpc2012, coefnorm = TRUE, weighting = pop2012, wmean = TRUE)
Vwn.ms[11, 1] <- Vwn
Vwn <- cv(pibpc2013, coefnorm = TRUE, weighting = pop2013, wmean = TRUE)
Vwn.ms[12, 1] <- Vwn
Vwn <- cv(pibpc2014, coefnorm = TRUE, weighting = pop2014, wmean = TRUE)
Vwn.ms[13, 1] <- Vwn
Vwn <- cv(pibpc2015, coefnorm = TRUE, weighting = pop2015, wmean = TRUE)
Vwn.ms[14, 1] <- Vwn

anos <- 2002:2015

# Plot Vw no tempo
plot(anos, Vwn.ms[, 1], "l", xlab = "Ano", ylab = "Vw normalizado do PIB per capita", 
    main = "Vw normalizado dos PIBs municipais per capita de MS, 2002-2015")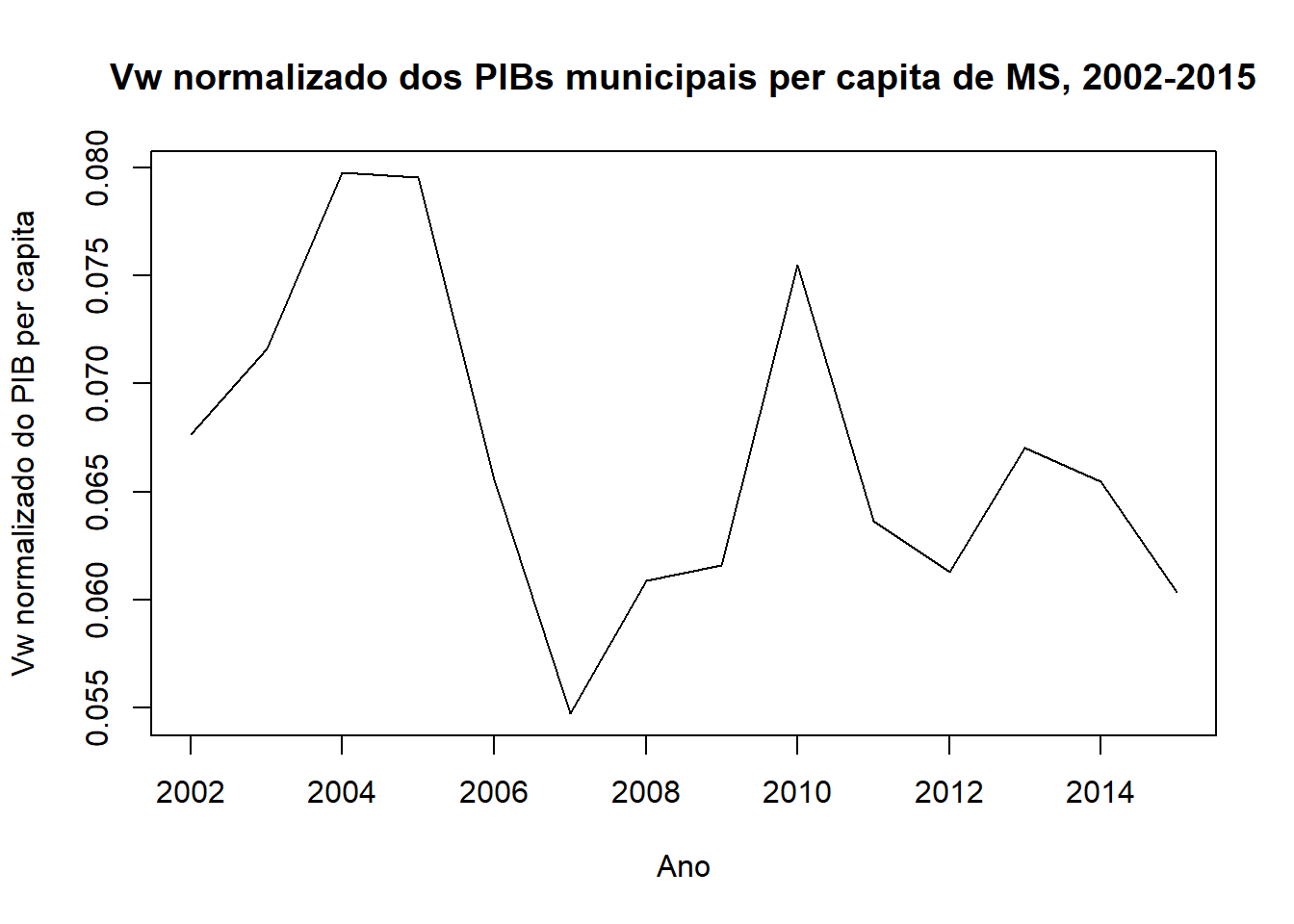

resultado.vwn <- as.data.frame(Vwn.ms)
rownames(resultado.vwn) <- anos
colnames(resultado.vwn) <- c("Vwn")
knitr::kable(resultado.vwn, caption = "Vw normalizado dos PIBs per capita municipais de MS, 2002-2015")

No caso normalizado, observam-se valores próximos a zero, indicando pequena variabilidade entre os municípios. Embora existam discrepâncias, o que pode ser detectado olhando estatísticas descritivas da série, percebe-se que a variabilidade entre os anos é muito pequena, não podendo dizer que são valores diferentes da média do período.

Índice de Theil

Este índice é comumento utilizado para avaliar a desigualdade entre extratos de renda ou, como aqui, entre localidades. A expressão básica é como abaixo.

\[ J = \sum\limits_r {\left( {\left( {\frac{{{p_r}}}{N}} \right)\ln \left( {\frac{{\frac{{{p_r}}}{N}}}{{\frac{{{Y_r}}}{Y}}}} \right)} \right)} \]

A expressão é a mesma do original de Theil et al (1996, p.12-13) e, neste caso: \(p_r\) é a população da localidade de análise \(r\); \(N\) é a população da localidade de referência; \(Y_r\) é o PIB per capita da localidade de análise \(r\); e \(Y\) é o PIB per capita da localidade de referência. No presente exemplo, a localidade de análise é o município e a de referência é o estado de MS.

Foi elaborada uma função para reproduzir essa expressão. Esclarecemos que o leitor deve ter cautela pois encontram-se outras expressões atribuídas como o índice de Theil, mas com rotinas que dão outros resultados, como por exemplo o da função REAT:::theil. A rotina da função utilizada (que nomeamos como theil.mon) é:

theil.mon <- function(x, y) {
    x_sum <- sum(x)
    y_sum <- sum(y)
    ln_sum <- log((y/y_sum)/(x/x_sum))
    J <- sum((y/y_sum) * ln_sum)
    return(J)
}

# x é o PIB per capita e y é a população
attach(pibpc)
attach(pop)
Theil.ms <- data.frame(matrix(0, nrow = 14, ncol = 1))
Theil <- theil.mon(pibpc2002, pop2002)
Theil.ms[1, 1] <- Theil
Theil <- theil.mon(pibpc2003, pop2003)
Theil.ms[2, 1] <- Theil
Theil <- theil.mon(pibpc2004, pop2004)
Theil.ms[3, 1] <- Theil
Theil <- theil.mon(pibpc2005, pop2005)
Theil.ms[4, 1] <- Theil
Theil <- theil.mon(pibpc2006, pop2006)
Theil.ms[5, 1] <- Theil
Theil <- theil.mon(pibpc2007, pop2007)
Theil.ms[6, 1] <- Theil
Theil <- theil.mon(pibpc2008, pop2008)
Theil.ms[7, 1] <- Theil
Theil <- theil.mon(pibpc2009, pop2009)
Theil.ms[8, 1] <- Theil
Theil <- theil.mon(pibpc2010, pop2010)
Theil.ms[9, 1] <- Theil
Theil <- theil.mon(pibpc2011, pop2011)
Theil.ms[10, 1] <- Theil
Theil <- theil.mon(pibpc2012, pop2012)
Theil.ms[11, 1] <- Theil
Theil <- theil.mon(pibpc2013, pop2013)
Theil.ms[12, 1] <- Theil
Theil <- theil.mon(pibpc2014, pop2014)
Theil.ms[13, 1] <- Theil
Theil <- theil.mon(pibpc2015, pop2015)

Theil.ms[14, 1] <- Theil
resultado.Theil.ms <- as.data.frame(Theil.ms)
rownames(resultado.Theil.ms) <- anos
colnames(resultado.Theil.ms) <- c("Theil.ms")
knitr::kable(resultado.Theil.ms, caption = "Theil dos PIBs per capita municipais de MS, 2002-2015")

# Plot Theil (Monasterio) no tempo
plot(anos, Theil.ms[, 1], "l", xlab = "Ano", ylab = "Theil do PIB per capita", main = "Theil dos PIBs municipais per capita de MS, 2002-2015")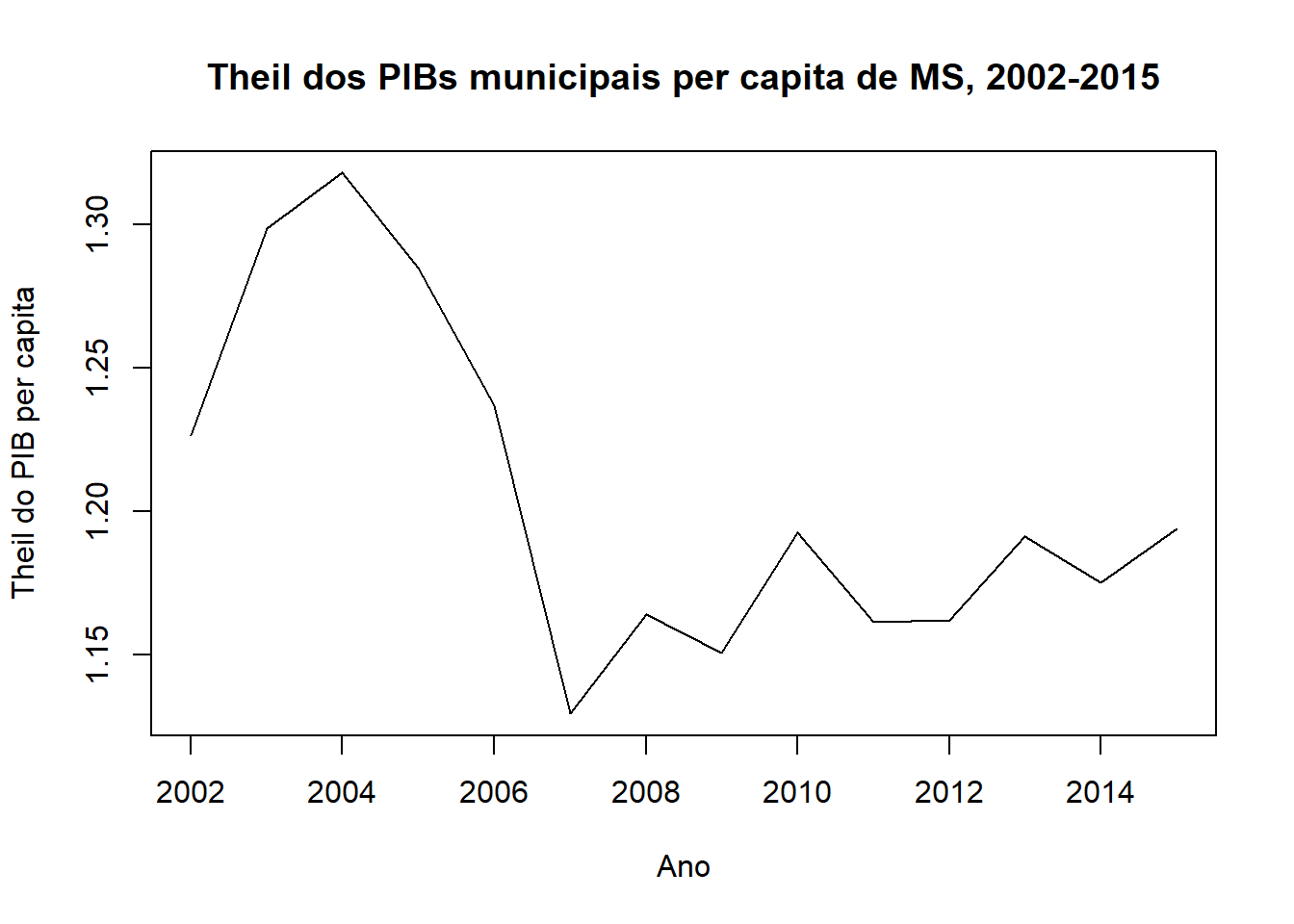

É possível ver que a desigualdade reduziu entre os municípios até 2007, aumentados nos anos seguintes.