Economia Regional: reprodução de medidas de LQ conforme Haddad (2018) em R
Licença
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0
Citação
Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: reprodução de medidas de LQ conforme Haddad (2018) em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/medidas_QL_haddad_regional.
Script para reprodução (se utilizar, citar como acima)
Download 2020-04-28-economia-regional-reprodução-de-medidas-de-lq.RmdIntrodução
A ideia básica deste arquivo é orientar os procedimentos para o cálculo dos indicadores de análise regional a saber:
- Quociente Locacional (QL)
Para esse exercício, tentaremos reproduzir os resultados das notas de aula do Prof. Eduardo Amaral Haddad (FEA-USP) utilizando o R (HADDAD, 2018). A base de dados de valores da produção das regiões e setores estão em http://www.usp.br/nereus/wp-content/uploads/Classic_Measures_Isard.xlsx.
Os slides de aula contendo algumas orientações para os cálculos em Excel estão em: http://www.usp.br/nereus/wp-content/uploads/Aula_1_Medidas3.pdf, Aula 1: Medidas de Concentração, Especialização e Localização. Os dados foram baixados e armazenados no mesmo diretório do projeto a fim de agilizar a rotina do RMarkdown. Entretanto, os usuários podem obtê-los fazendo uso do R conforme segue.
# Executar uma vez para baixar xlsx
require(readxl)
suppressMessages(suppressWarnings(library(httr)))
url1 <- "http://www.usp.br/nereus/wp-content/uploads/Classic_Measures_Isard.xlsx"
download.file(url1, destfile = "Classic_Measures_Isard.xlsx", mode = "wb")Após realizar o download, chamei os dados para o RStudio a partir da planilha .xlsx e fiz um dput() do objeto para colocá-lo “embedded” para vocês. É só baixar o script deste Markdown e vocês conseguirão acesso direto aos dados. Eles ficarão “omitidos” deste post apenas para economizar espaço e dar maior clareza ao texto.
require(readxl)
Classic_Measures_Isard <- read_excel("Classic_Measures_Isard.xlsx", sheet = "Basic data")knitr::kable(Classic_Measures_Isard)| …1 | GRP ($) | T0 | …4 | …5 | …6 | …7 | …8 | T1 | …10 | …11 | …12 | …13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NA | NA | Agropecuária | Indústria | Comércio | Serviços | Total | NA | Agropecuária | Indústria | Comércio | Serviços | Total |
| NA | NA | Sector 1 | Sector 2 | Sector 3 | Sector 4 | Total | NA | Sector 1 | Sector 2 | Sector 3 | Sector 4 | Total |
| Alto da Serra do Botucarai | Region 1 | 220053 | 130186 | 51951 | 257288 | 659478 | NA | 325910 | 74098 | 60098 | 346776 | 806882 |
| Alto Jacuí | Region 2 | 371700 | 181517 | 193490 | 512116 | 1258823 | NA | 600900 | 316868 | 225256 | 604406 | 1747430 |
| Campanha | Region 3 | 272657 | 353027 | 151697 | 594083 | 1371464 | NA | 496665 | 419698 | 110750 | 756107 | 1783220 |
| Central | Region 4 | 657885 | 368199 | 349747 | 1101841 | 2477672 | NA | 963289 | 410927 | 337248 | 1693444 | 3404908 |
| Centro Sul | Region 5 | 258225 | 442363 | 112930 | 603659 | 1417177 | NA | 492656 | 549847 | 109794 | 830967 | 1983264 |
| Fronteira Noroeste | Region 6 | 423025 | 390987 | 174935 | 597926 | 1586873 | NA | 607335 | 810284 | 175961 | 738405 | 2331985 |
| Fronteira Oeste | Region 7 | 991381 | 821440 | 339365 | 1362000 | 3514186 | NA | 1660779 | 574961 | 304911 | 1829345 | 4369996 |
| Hortênsias | Region 8 | 150874 | 450009 | 101102 | 448444 | 1150429 | NA | 318804 | 402015 | 121340 | 729000 | 1571159 |
| Jacuí Centro | Region 9 | 293263 | 169753 | 80674 | 375691 | 919381 | NA | 401551 | 182875 | 67241 | 477883 | 1129550 |
| Litoral | Region 10 | 188364 | 982884 | 116823 | 593524 | 1881595 | NA | 280503 | 111867 | 130511 | 1056953 | 1579834 |
| Médio Alto Uruguai | Region 11 | 398996 | 64274 | 70034 | 447968 | 981272 | NA | 688040 | 73668 | 69889 | 614622 | 1446219 |
| Metropolitano do Delta do Jacuí | Region 12 | 279598 | 7691794 | 2695132 | 6219614 | 16886138 | NA | 216072 | 10594289 | 3113935 | 8920807 | 22845103 |
| Missões | Region 13 | 670035 | 132424 | 218736 | 724656 | 1745851 | NA | 700415 | 194369 | 189215 | 869011 | 1953010 |
| Nordeste | Region 14 | 390443 | 80229 | 76235 | 328507 | 875414 | NA | 680983 | 144002 | 91234 | 472199 | 1388418 |
| Noroeste Colonial | Region 15 | 575910 | 291903 | 316887 | 900938 | 2085638 | NA | 912746 | 550781 | 331355 | 1074358 | 2869240 |
| Norte | Region 16 | 406216 | 287595 | 175096 | 540078 | 1408985 | NA | 580619 | 511881 | 227217 | 796057 | 2115774 |
| Paranhana-Encosta da Serra | Region 17 | 44437 | 1097552 | 70140 | 414765 | 1626894 | NA | 92512 | 1145229 | 61508 | 702725 | 2001974 |
| Produção | Region 18 | 707211 | 615895 | 483704 | 1087379 | 2894189 | NA | 1329927 | 1292666 | 560299 | 1538345 | 4721237 |
| Serra | Region 19 | 699135 | 4876259 | 590661 | 2190060 | 8356115 | NA | 1582022 | 6839600 | 674397 | 3325393 | 12421412 |
| Sul | Region 20 | 766464 | 2460276 | 623724 | 2107097 | 5957561 | NA | 1021789 | 2330732 | 504801 | 2737676 | 6594998 |
| Vale do Caí | Region 21 | 226397 | 552646 | 74365 | 404443 | 1257851 | NA | 266483 | 1101963 | 82583 | 612882 | 2063911 |
| Vale do Rio dos Sinos | Region 22 | 40498 | 9802363 | 1432091 | 3463830 | 14738782 | NA | 56371 | 11149161 | 1783098 | 4700108 | 17688738 |
| Vale do Rio Pardo | Region 23 | 623789 | 2013393 | 242800 | 991438 | 3871420 | NA | 1045464 | 2460486 | 214486 | 1469228 | 5189664 |
| Vale do Taquari | Region 24 | 446825 | 1613726 | 191357 | 853003 | 3104911 | NA | 848427 | 2163499 | 223363 | 1227532 | 4462821 |
| NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Total do Rio Grande do Sul | Total | 10103381 | 35870694 | 8933676 | 27120348 | 82028099 | NA | 16170262 | 44405766 | 9770490 | 38124229 | 108470747 |
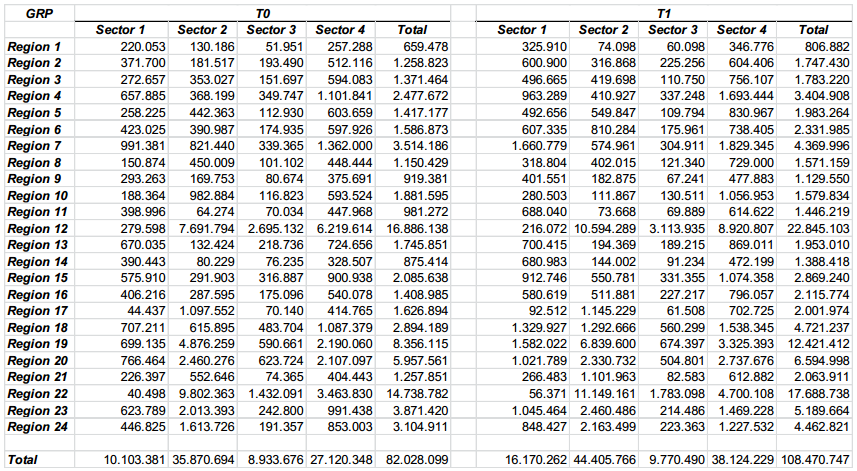
Tela dos dados básicos para realizar Quociente Locacional
Procedimentos
Quociente Locacional (QL)
O Quociente Locacional (QL) é uma medida que dá a informação de qual o setor mais representado no município (região de análise) quando comparado com o mesmo setor no estado (região de referência). Foi elaborado inicialmente por Haig (1928) e vem sendo muito utilizado em várias análises regionais e de localização industrial. Também chamado de Índice de Revealed Comparative Advantage (RCA – ou Vantagem comparativa revelada, VCR) seguindo Balasa (1965), ou índice de Hoover-Balassa.
A expressão básica é:
\[ QL_{ki}=\left( {\frac{{\frac{{{E_{ki}}}}{E_i}}}{{\frac{{{E_k}}}{E}}}} \right) \] em que: \({E_{ki}}\) é o emprego no setor \(k\) na localidade de análise \(i\); \({E_i}\) é o emprego total na localidade de análise \(i\); \({E_k}\) é o emprego no setor \(k\) da localidade de referência; e \(E\) é o emprego total da localidade de referência.
A ideia é saber se na localidade de análise, a proporção do emprego do setor é maior ou menor que esta proporção no local de referência. Assim, se o resultado for maior que hum \(\left( {QL_{ki}}\gt 1\right)\), então diz-se que a localidade de análise é relativamente mais especializada nesse setor que a localidade de refência. De outro lado, valores menores que a unidade \(\left( {QL_{ki}}\lt 1\right)\) indicam que a localidade analisada tem representação menor deste setor do que a representação deste na localidade de referência.
A representação de Haddad (2018) é no mesmo sentido, apenas a diferença é que invés de mencionar o emprego como variável, ele coloca produção. Isso é realizado em vários estudos, principalmente nos do tipo insumo-produto, quando se colocam os valores de valor adicionado. Em alguns estudos encontramos também versões com a produção agrícola, ou ainda os valores de exportações para a análoga da vantagem comparativa revelada de Balassa. A fórmula da nota de aula de Haddad (2018), portanto, é a mesma, apenas com indicação algébrica alterada para \(R_i\) e \(N_i\) para indicar a região (R) e o país (N) no setor i, a saber:
\[ QL_{i}=\left( {\frac{{\frac{{{R_{i}}}}{N_i}}}{{\frac{{{R}}}{N}}}} \right)=\left( {\frac{{\frac{{{R_{i}}}}{R}}}{{\frac{{{N_i}}}{N}}}} \right) \]
em que: \({R_i}\) é a produção no setor \(i\) na localidade de análise; \({R}\) é a produção total na localidade de análise; \({N_i}\) é a produção no setor \(i\) da localidade de referência (do país); e \(N\) é a produção total da localidade de referência (do país).
É interessante olhar estas razões (ou shares), pois no cálculo exemplificado em Excel, ficarão evidenciadas as operações matemáticas.
EconGeo de Balland (2017)
Esta rotina pode ser resumida fazendo o uso do pacote EconGeo, e a função RCA para obter o Quociente Locacional (similar ao Revealed Comparative Advantage - RCA - índice de Balassa, 1965). O pacote pode ser instalado fazendo como a seguir:
install.packages("devtools")
library(devtools)
devtools::install_github("PABalland/EconGeo", force = T)Ela utiliza uma matriz contendo os dados no formato abaixo, em que \((I1,I2,I3)\) são as indústrias ou setores, para os municípios \((R1,R2,R3)\).
municipio |I1 |I2 | I3
-----------|---------|--------|------------
R1 |100 |150 | 165
R2 |130 |400 | 220
R3 |200 |1200 | 20Prepararemos os dados para os cálculos, construindo uma matriz mat para os dados de medidas clássicas de Isard:
library(EconGeo)
## gerar a matriz industrial da região, para T0
set.seed(31)
mat_0 <- as.matrix(Classic_Measures_Isard[3:26, 3:6])
rownames(mat_0) <- c("R1", "R2", "R3", "R4", "R5", "R6", "R7", "R8", "R9", "R10",
"R11", "R12", "R13", "R14", "R15", "R16", "R17", "R18", "R19", "R20", "R21",
"R22", "R23", "R24")
colnames(mat_0) <- c("setor1", "setor2", "setor3", "setor4")O cálculo do Quociente Locacional (QL = RCA) será fazendo:
class(mat_0) <- "numeric"
QL_T0 <- round(RCA(mat_0), digits = 4)Você pode comparar esse resultado com o da planilha LQ1, onde os cálculos forma feitos em fórmulas do Excel. Similarmente fizemos para T1 e depois colocamos tudo em uma só tabela.
library(EconGeo)
## gerar a matriz industrial da região, para T0
set.seed(31)
mat_1 <- as.matrix(Classic_Measures_Isard[3:26, 9:12])
rownames(mat_1) <- c("R1", "R2", "R3", "R4", "R5", "R6", "R7", "R8", "R9", "R10",
"R11", "R12", "R13", "R14", "R15", "R16", "R17", "R18", "R19", "R20", "R21",
"R22", "R23", "R24")
colnames(mat_1) <- c("setor1", "setor2", "setor3", "setor4")
class(mat_1) <- "numeric"
QL_T1 <- round(RCA(mat_1), digits = 4)LQ1 <- cbind(QL_T0, QL_T1)
knitr::kable(LQ1, caption = "Quociente Locacional em T0 e T1")| setor1 | setor2 | setor3 | setor4 | setor1 | setor2 | setor3 | setor4 | |
|---|---|---|---|---|---|---|---|---|
| R1 | 2.7091 | 0.4514 | 0.7233 | 1.1800 | 2.7095 | 0.2243 | 0.8269 | 1.2228 |
| R2 | 2.3973 | 0.3297 | 1.4113 | 1.2305 | 2.3067 | 0.4429 | 1.4311 | 0.9841 |
| R3 | 1.6141 | 0.5886 | 1.0156 | 1.3102 | 1.8683 | 0.5749 | 0.6895 | 1.2064 |
| R4 | 2.1558 | 0.3398 | 1.2961 | 1.3451 | 1.8978 | 0.2948 | 1.0996 | 1.4151 |
| R5 | 1.4793 | 0.7138 | 0.7317 | 1.2884 | 1.6663 | 0.6772 | 0.6146 | 1.1921 |
| R6 | 2.1643 | 0.5634 | 1.0122 | 1.1397 | 1.7470 | 0.8488 | 0.8377 | 0.9009 |
| R7 | 2.2904 | 0.5345 | 0.8867 | 1.1722 | 2.5493 | 0.3214 | 0.7746 | 1.1910 |
| R8 | 1.0648 | 0.8945 | 0.8069 | 1.1790 | 1.3611 | 0.6250 | 0.8574 | 1.3201 |
| R9 | 2.5897 | 0.4222 | 0.8057 | 1.2360 | 2.3847 | 0.3955 | 0.6609 | 1.2037 |
| R10 | 0.8128 | 1.1945 | 0.5701 | 0.9541 | 1.1910 | 0.1730 | 0.9171 | 1.9035 |
| R11 | 3.3012 | 0.1498 | 0.6553 | 1.3808 | 3.1914 | 0.1244 | 0.5365 | 1.2092 |
| R12 | 0.1344 | 1.0416 | 1.4655 | 1.1140 | 0.0634 | 1.1328 | 1.5133 | 1.1110 |
| R13 | 3.1159 | 0.1735 | 1.1504 | 1.2554 | 2.4057 | 0.2431 | 1.0756 | 1.2660 |
| R14 | 3.6211 | 0.2096 | 0.7996 | 1.1350 | 3.2901 | 0.2534 | 0.7295 | 0.9676 |
| R15 | 2.2419 | 0.3201 | 1.3951 | 1.3065 | 2.1339 | 0.4689 | 1.2821 | 1.0654 |
| R16 | 2.3407 | 0.4668 | 1.1410 | 1.1594 | 1.8408 | 0.5910 | 1.1923 | 1.0705 |
| R17 | 0.2218 | 1.5427 | 0.3959 | 0.7711 | 0.3100 | 1.3974 | 0.3411 | 0.9987 |
| R18 | 1.9839 | 0.4866 | 1.5346 | 1.1364 | 1.8896 | 0.6688 | 1.3175 | 0.9271 |
| R19 | 0.6793 | 1.3345 | 0.6490 | 0.7927 | 0.8544 | 1.3450 | 0.6028 | 0.7617 |
| R20 | 1.0445 | 0.9444 | 0.9613 | 1.0698 | 1.0393 | 0.8633 | 0.8498 | 1.1811 |
| R21 | 1.4613 | 1.0047 | 0.5428 | 0.9725 | 0.8661 | 1.3042 | 0.4442 | 0.8449 |
| R22 | 0.0223 | 1.5209 | 0.8922 | 0.7108 | 0.0214 | 1.5396 | 1.1191 | 0.7560 |
| R23 | 1.3082 | 1.1893 | 0.5759 | 0.7746 | 1.3513 | 1.1581 | 0.4588 | 0.8055 |
| R24 | 1.1684 | 1.1885 | 0.5659 | 0.8309 | 1.2753 | 1.1842 | 0.5556 | 0.7826 |
E agora reproduzimos a tela do Excel, pasta “LQ1”, previamente calculado para conferência.
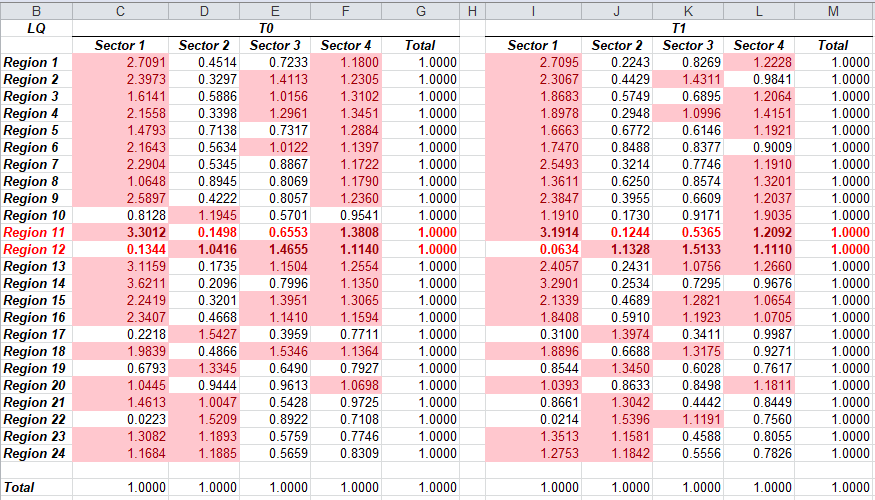
Resultados da planilha em MS Excel para LQ1
Exemplificando pelo Excel
Acompanhando a notação da nota de aula de Haddad (2018), coloco as imagens do procedimento realizado no Excel. Para recordar, a expressão é
\[
QL_{i}=\left( {\frac{{\frac{{{R_{i}}}}{N_i}}}{{\frac{{{R}}}{N}}}} \right)=\left( {\frac{{\frac{{{R_{i}}}}{R}}}{{\frac{{{N_i}}}{N}}}} \right)
\]
LQ1
Passo 1: calcular as parcelas regionais (regional shares). Desta forma, o primeiro passo será obter \(\frac{R_i}{N_i}\).O procedimento começa fazendo as contas do valor (para a célula C4) igual a ='Basic data'!C4/'Basic data'!C$29. Ou seja, a célula C4 (produção da Region1 Sector1 em ‘Basic data’) dividido pela célula C29 (produção Total Sector1 em ‘Basic data’). Os cálculos seguem para as demais células e encorajamos o leitor a fazer a checagem na planilha.
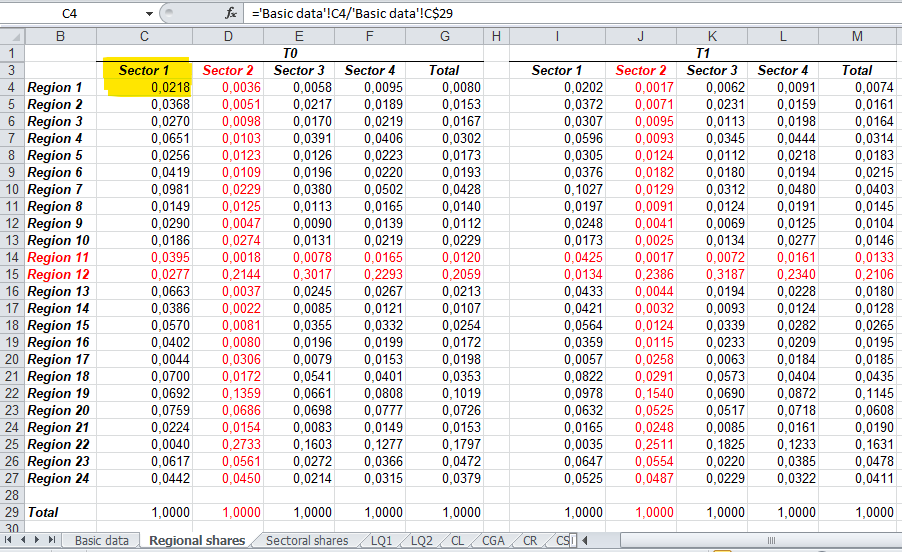
Cálculo do share regional
O resultado obtido na coluna G, em Regional Shares, indica a parcela da região 1 no total (='Basic data'!G4/'Basic data'!G$29 em ‘Regional Shares’).
Passo 2: O resultado da coluna G será o denominador da expressão de \(QL_i\). Ou seja, passamos então ao passo 2 que é efetivamente o cálculo do QL.

Cálculo do quociente locacional - LQ1
O cálculo do valor (para a célula C4) igual a ='Regional shares'!C4/'Regional shares'!$G4. Ou seja, a célula C4 (‘Regional shares’ da Region1 Sector1) dividido pela célula G4 de ‘Regional shares’ (o share total).
LQ2
O cálculo semelhante é feito por Haddad (2018) em LQ2 para evidenciar que fazendo pelo share setorial dará resultado igual, mas deve-se atentar pela alteração do sentido.
Passo 1 para LQ2: Neste LQ2, o cálculo será pela linha (ou seja, \(R_i/R\). Na planilha ‘Sectoral shares’, você encontrará em C4 a fórmula: ='Basic data'!C4/'Basic data'!$G4, ou seja, agora divide-se a coluna C por G fazendo o sectoral share. A linha 29 dará o denominador \(N_i/N\).
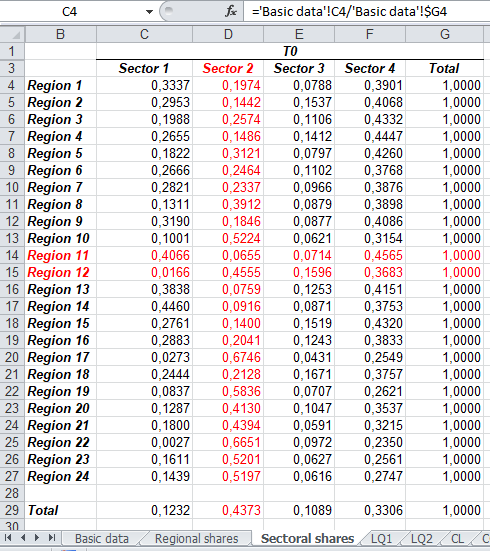
Cálculo do share setorial
Passo 2 para LQ2: agora faz-se o cálculo do quociente locacional usando a fórmula, para a célula C4, ='Sectoral shares'!C4/'Sectoral shares'!C$29, ou seja, o share setorial da região dividido pelo share setorial do país (total).
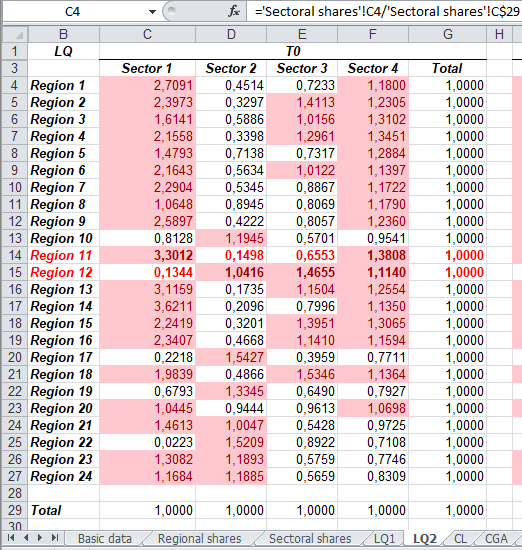
Cálculo do quociente locacional - LQ2
Referências
BALASSA, B. Trade Liberalization and Revealed Comparative Advantage, The Manchester School 33: 99-123. 1965.
BALLAND, P.A. Economic Geography in R: Introduction to the EconGeo Package, Papers in Evolutionary Economic Geography, 17 (09): 1-75, 2017.
CRUZ, B.O.; QUEIROZ, I.V. Efeitos encadeados do perfil setorial dos investimentos e a distribuição espacial da indústria: onde se localizam as indústrias dos setores com maiores impactos? Texto para discussão n. 2172, Brasília: IPEA, 2016.
FLORENCE, P. Sargent. Investment, location, and size of plant. Cambridge: Cambridge University Press, 1948.
HADDAD, Eduardo Amaral. Aula 1: Medidas de Concentração, Especialização e Localização. In: HADDAD, E.A. Métodos de Análise Regional e Inter-regional. Departamento de Ciências Econômicas/UEMS, Ponta Porã - MS, 13 e 14 de junho de 2018. São Paulo: NEREUS-FEA-USP, 2018. Disponível em: http://www.usp.br/nereus/wp-content/uploads/Aula_1_Medidas3.pdf. Acesso em 27 Abr 2020.
HADDAD, Paulo R. (org.) (1989). Economia Regional: Teorias e Métodos de Análise. Banco do Nordeste, Fortaleza, cap. 4.
MONASTERIO, Leonardo. Indicadores de análise regional e espacial. In: CRUZ et al (orgs). Economia regional e urbana : teorias e métodos com ênfase no Brasil. Brasília: Ipea, 2011. cap. 10. pp.315-331.
NORTH, Douglas. Teoria da localização e crescimento econômico regional. In: SCWARTZMANN, J. (org.) Economia regional e urbana: tetos escolhidos. Belo Horizonte: UFMG, p.333-343, 1977.
SOUZA, Filipe Lage de. A localização da indústria de transformação brasileira nas últimas três décadas. Rio de Janeiro: EPGE-FGV, 2002. (Dissertação, Mestrado em Economia). 130p.