Séries Temporais com R: Análise do consumo de Morettin e Toloi com X13ARIMA-SEATS
Licença
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0
As ideias aqui expressas são de responsabilidade exclusiva do autor, e não representam as opiniões da instituição a que pertence.
Citação
Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Séries Temporais com R: Análise do consumo Morettin com X13ARIMA-SEATS. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/consumo_morettin_x13 e e https://adrianofigueiredo.netlify.app/post/séries-temporais-com-r-análise-do-consumo-de-morettin-e-toloi-com-x13arima-seats/.
Script para reprodução (se utilizar, citar como acima)
Download 2020-04-14-séries-temporais-com-r-análise-do-consumo-de-morettin-e-toloi-com-x13arima-seats.RmdIntrodução
Os dados vem do livro de Morettin e Toloi, Análise de Séries Temporais (https://www.ime.usp.br/~pam/ST.html), consumo no varejo de São Paulo, mensais de Jan/1984 a Out/1996, em https://www.ime.usp.br/~pam/CONSUMO.XLS.
library(readxl)
library(fpp2)
# consumo morettin e toloi dados <- read_excel('CONSUMO morettin R.xlsx',sheet =
# 'dados')
dados <- structure(list(consumo = c(114.13, 110.79, 116.46, 111.57, 120.66, 121.15,
121.27, 127.02, 129.04, 133.3, 130.6, 179.39, 120.64, 114.05, 130.6, 118.26,
145.54, 135.13, 153.35, 159.95, 150.01, 164.93, 170.37, 220.96, 134.26, 133.11,
147.84, 164.46, 181.86, 170.44, 186.64, 174.21, 181.62, 194.16, 181.9, 232.01,
140.16, 130.78, 119.04, 120.73, 129.81, 111.04, 122.75, 133.95, 125.41, 132.05,
129.54, 176.37, 110.09, 113.25, 124.03, 110.63, 116.72, 124.63, 124.38, 130.27,
119.87, 115.75, 122.44, 162.43, 105.89, 115.59, 147, 131.7, 131.32, 136.66, 126.43,
134.88, 128.26, 125.32, 124.61, 166.11, 116.25, 96.93, 89.27, 101.87, 125.57,
113.31, 109.39, 127.33, 120.56, 117.73, 113.81, 147.25, 100.15, 95.11, 112.26,
109.39, 114.2, 113.8, 126.47, 128.36, 115.71, 116.09, 99.53, 127.27, 87.08, 85.67,
82.02, 98.2, 96.44, 90.23, 97.15, 95.08, 94, 93, 96.09, 129.21, 75.39, 77.7,
97.34, 84.97, 87.55, 86.64, 90.52, 95.4, 95.2, 95.8, 101.23, 128.49, 85.63, 82.77,
96.55, 81.33, 96.91, 83.76, 90.19, 114.84, 108.4, 106.05, 109.71, 143.86, 99.12,
99.28, 114.75, 106.13, 110.02, 108.07, 112.52, 113.87, 107.84, 112.12, 112.03,
139.37, 92.24, 93.56, 107.37, 102.89, 114.78, 102.88, 118.41, 119.23, 117.36,
122.06)), row.names = c(NA, -154L), class = c("tbl_df", "tbl", "data.frame"))
# consumo.ts<-ts(dados,start = c(1984,1),frequency = 12) coloquei opção do dput()
# a seguir
consumo.ts <- structure(c(114.13, 110.79, 116.46, 111.57, 120.66, 121.15, 121.27,
127.02, 129.04, 133.3, 130.6, 179.39, 120.64, 114.05, 130.6, 118.26, 145.54,
135.13, 153.35, 159.95, 150.01, 164.93, 170.37, 220.96, 134.26, 133.11, 147.84,
164.46, 181.86, 170.44, 186.64, 174.21, 181.62, 194.16, 181.9, 232.01, 140.16,
130.78, 119.04, 120.73, 129.81, 111.04, 122.75, 133.95, 125.41, 132.05, 129.54,
176.37, 110.09, 113.25, 124.03, 110.63, 116.72, 124.63, 124.38, 130.27, 119.87,
115.75, 122.44, 162.43, 105.89, 115.59, 147, 131.7, 131.32, 136.66, 126.43, 134.88,
128.26, 125.32, 124.61, 166.11, 116.25, 96.93, 89.27, 101.87, 125.57, 113.31,
109.39, 127.33, 120.56, 117.73, 113.81, 147.25, 100.15, 95.11, 112.26, 109.39,
114.2, 113.8, 126.47, 128.36, 115.71, 116.09, 99.53, 127.27, 87.08, 85.67, 82.02,
98.2, 96.44, 90.23, 97.15, 95.08, 94, 93, 96.09, 129.21, 75.39, 77.7, 97.34,
84.97, 87.55, 86.64, 90.52, 95.4, 95.2, 95.8, 101.23, 128.49, 85.63, 82.77, 96.55,
81.33, 96.91, 83.76, 90.19, 114.84, 108.4, 106.05, 109.71, 143.86, 99.12, 99.28,
114.75, 106.13, 110.02, 108.07, 112.52, 113.87, 107.84, 112.12, 112.03, 139.37,
92.24, 93.56, 107.37, 102.89, 114.78, 102.88, 118.41, 119.23, 117.36, 122.06),
.Dim = c(154L, 1L), .Dimnames = list(NULL, "consumo"), .Tsp = c(1984, 1996.75,
12), class = "ts")
(consumo.ts)
attach(dados)
plot(consumo.ts)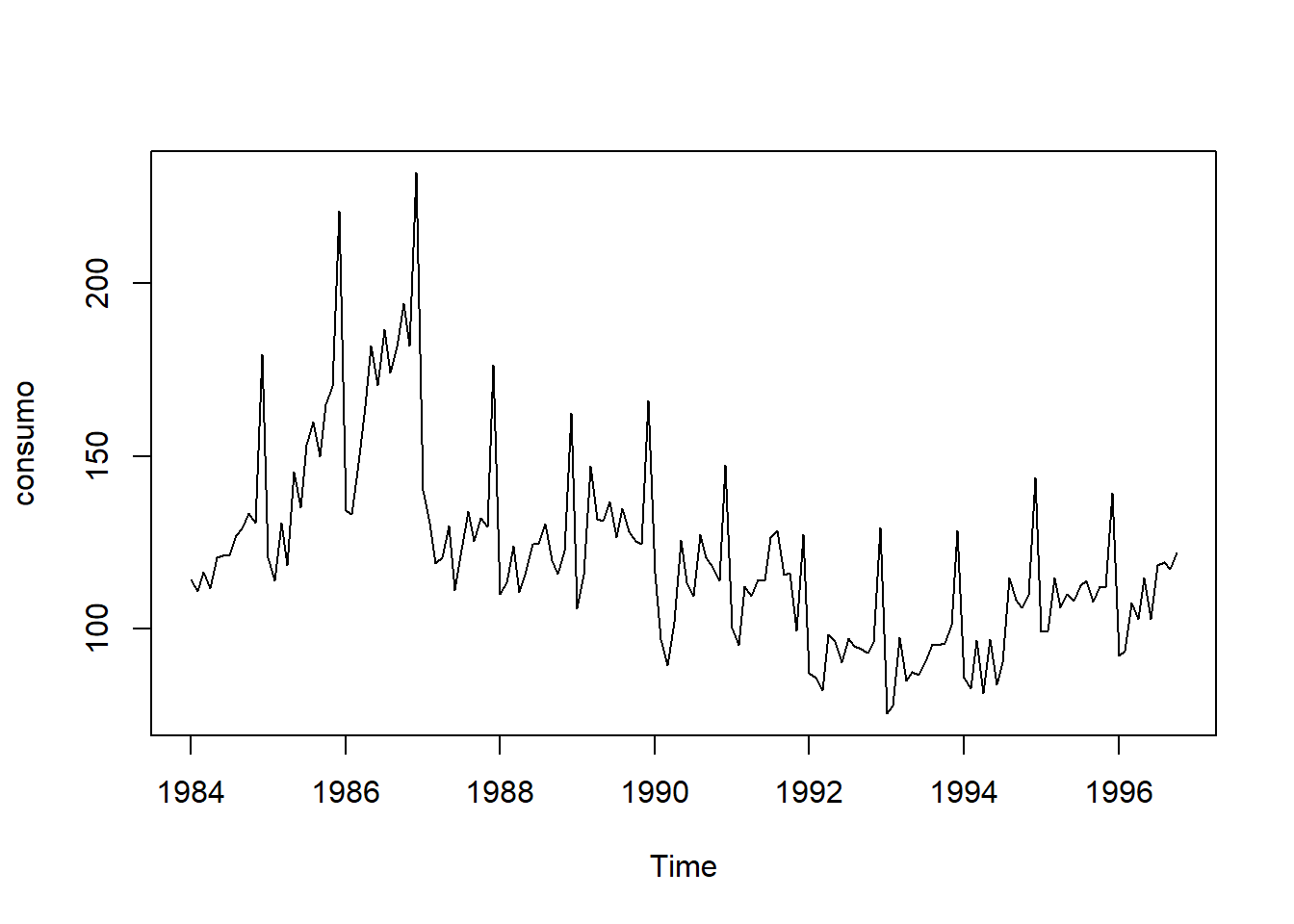
# Census x13-Arima-Seats ##############################
# informando ao RStudio onde estão os arquivos para o x13as local <-
# paste0(getwd(), '/x13as') Sys.setenv(X13_PATH = local)
library(seasonal)
library(seasonalview) #chamando o pacote
checkX13() #checagem se o x13 está operacional no RStudio
# vou então gerar as análises fazendo como em SAX(2017) e FERREIRA e MATTOS
# (2016) RELEMBRANDO o gráfico da série
plot(consumo.ts, xlab = "Tempo")
abline(h = seq(70, 230, 5), v = seq(1984, 1997, 1), lty = 3, col = "darkgrey")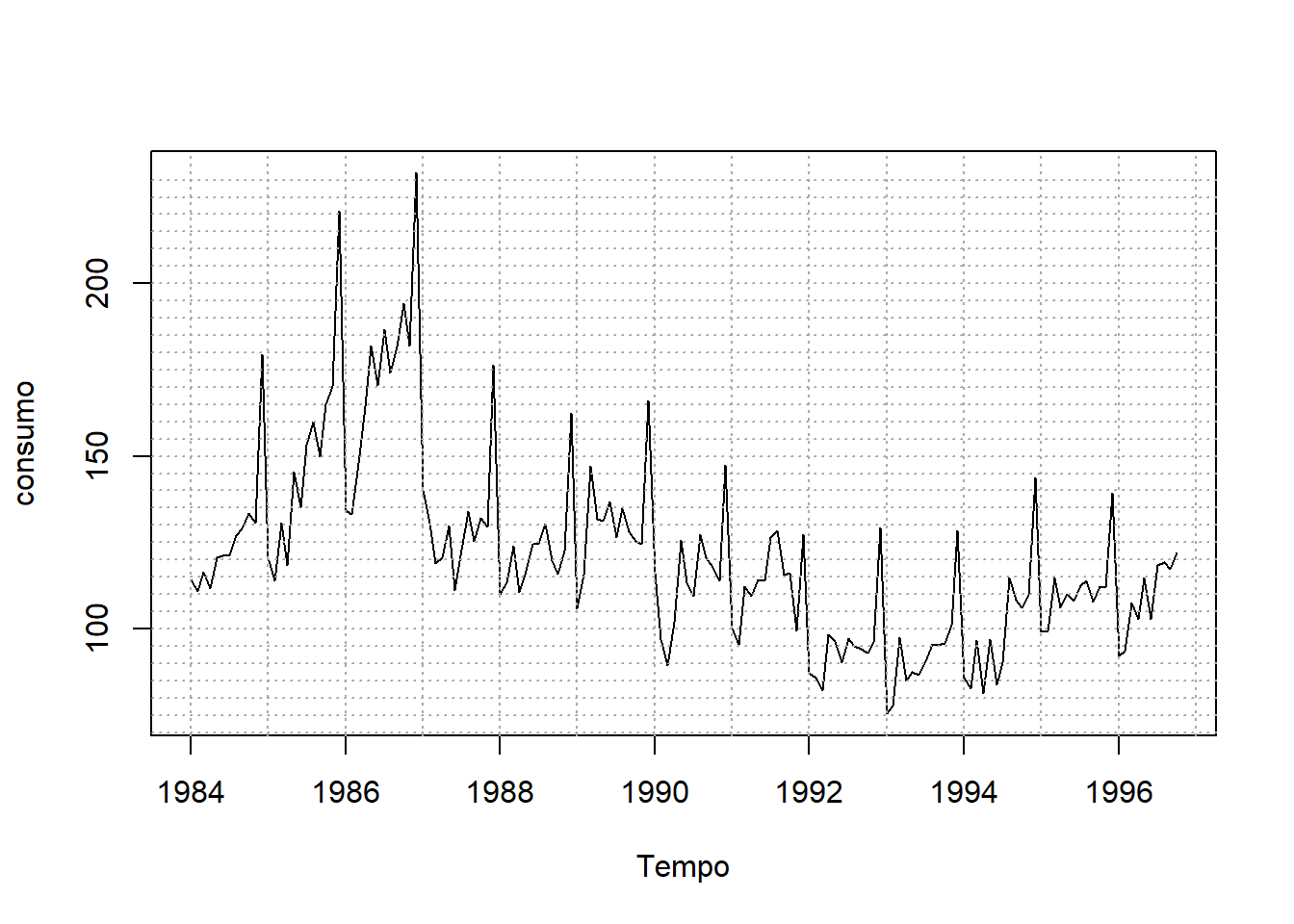
monthplot(consumo.ts, labels = month.abb, lty.base = 2)
legend("topleft", legend = c("consumo/mes", "media/mes"), cex = 0.8, lty = c(1, 2),
bty = "n")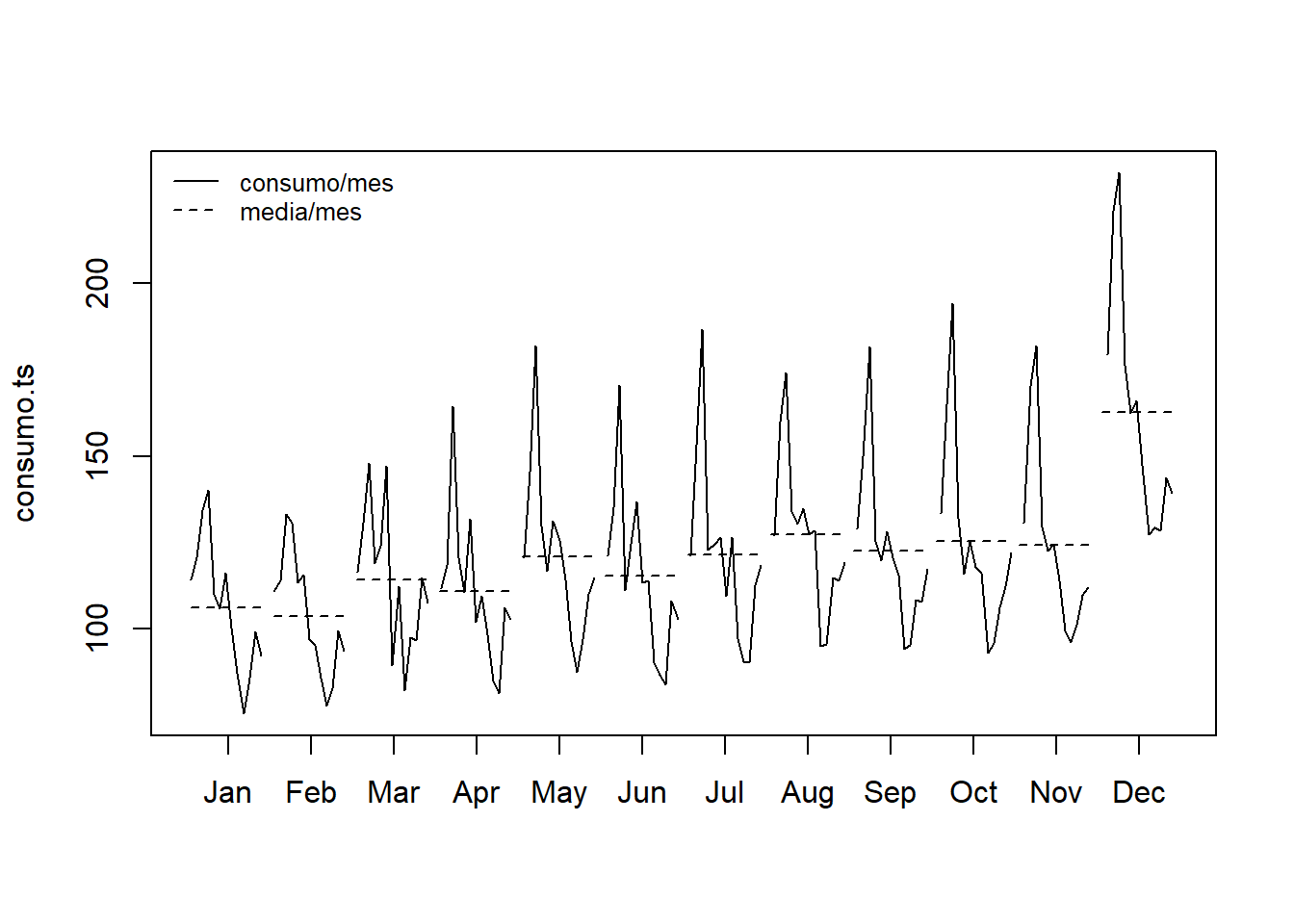
options(digits = 6)Modelo automático
# rodando o automático
ajuste <- seas(x = consumo.ts) # rodou x13O modo Shiny do seasonalview
Ele abre um apps Shiny para auxiliar a modelagem e visualização. Ver figura abaixo de como sai o modelo ‘ajuste’.
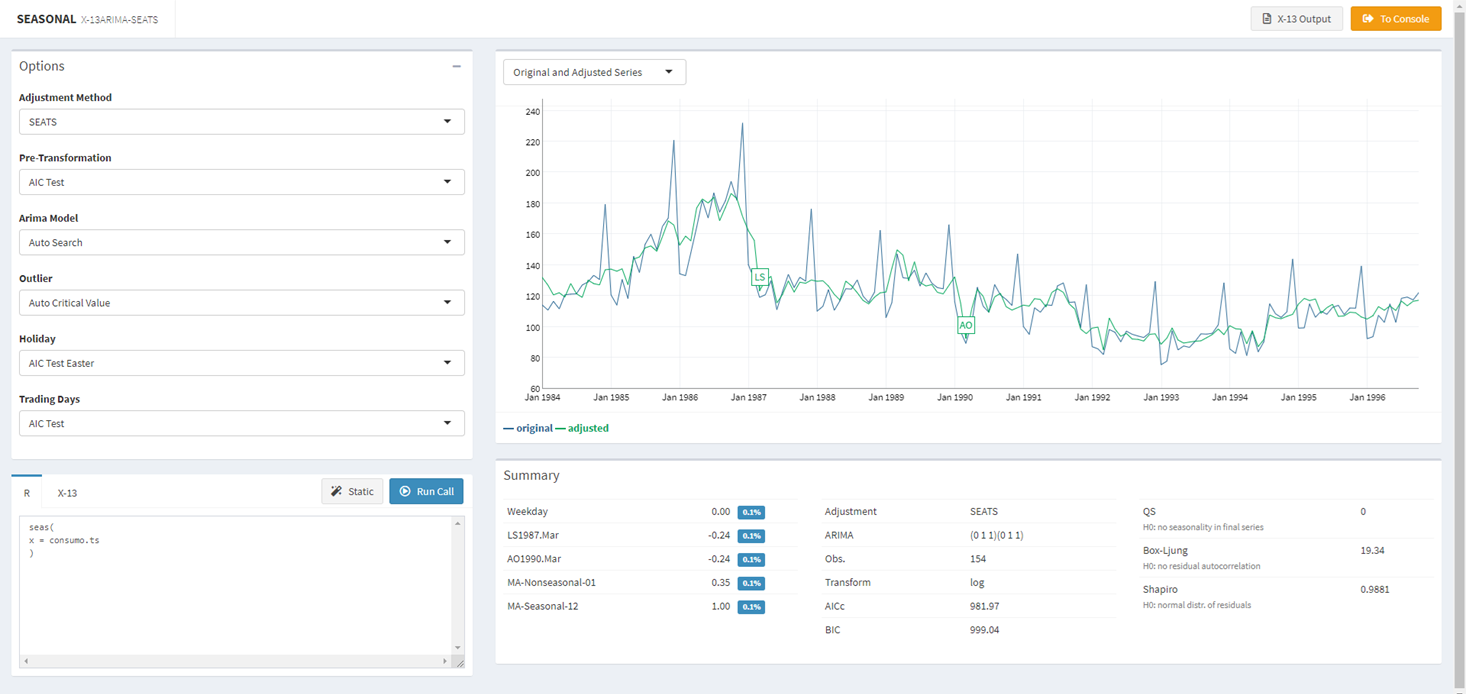
Figura da tela do Shiny apps do seasonalview.
# not run
view(ajuste) #seasonalviewAvaliação do automático
A avaliação do modelo ‘automático’ (sem alterar as especificações default) compreende as etapas: 1. Verificar teste de sazonalidade QS; 2. Diagnosticar pré-ajuste e modelo ARIMA; 3. Verificar indícios de sazonalidade ou efeitos de dias úteis graficamente; 4. Avaliar a estabilidade do ajuste sazonal;
# specserie<-spec.ar(consumo.ts) specserie
options(digits = 6)
qs(ajuste) # faz o teste QS para sazonalidade qs p-val
qsori 198.629 0
qsorievadj 217.851 0
qsrsd 0.000 1
qssadj 0.000 1
qssadjevadj 0.000 1
qsirr 0.000 1
qsirrevadj 0.000 1
qssori 103.976 0
qssorievadj 110.445 0
qssrsd 0.000 1
qsssadj 0.000 1
qsssadjevadj 0.000 1
qssirr 0.000 1
qssirrevadj 0.000 1summary(ajuste) # mostra os resultados da estimação ARIMA automatica e outliers detectados
Call:
seas(x = consumo.ts)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Weekday 0.00466 0.00121 3.84 0.00012 ***
LS1987.Mar -0.24369 0.05612 -4.34 1.4e-05 ***
AO1990.Mar -0.23999 0.04906 -4.89 1.0e-06 ***
MA-Nonseasonal-01 0.34581 0.07059 4.90 9.6e-07 ***
MA-Seasonal-12 0.99999 0.06674 14.98 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 154 Transform: log
AICc: 982, BIC: 999 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 19.3 Shapiro (normality): 0.988 final(ajuste) # mostra a serie ajustada Jan Feb Mar Apr May Jun Jul Aug
1984 132.0328 126.9387 120.6406 122.0129 119.2917 128.0256 121.4151 119.0353
1985 137.3050 135.9735 137.5141 127.2347 143.8890 145.1491 151.0475 152.3614
1986 152.8074 158.6975 155.6659 176.9392 182.7553 180.1137 183.8377 168.6748
1987 162.1477 155.9190 123.3108 129.8898 132.5961 115.4431 120.9073 129.6933
1988 129.4560 129.7558 126.3976 120.9811 117.2953 129.5719 126.5784 122.0786
1989 122.5011 137.8071 149.8041 146.3914 129.8308 142.0791 128.6648 126.3979
1990 132.3087 115.5603 92.4696 111.4004 124.1462 119.7428 109.5213 119.3218
1991 113.9848 113.3899 118.1968 117.6868 112.9054 122.2411 124.5714 122.2657
Sep Oct Nov Dec
1984 130.1792 127.9379 127.1244 136.8745
1985 148.8846 158.2958 168.5654 165.8639
1986 177.3393 186.3507 182.9360 171.3404
1987 122.4544 128.8257 128.1700 130.2513
1988 117.0449 114.7832 119.1854 121.9321
1989 127.2974 122.2619 121.2988 126.7478
1990 121.6234 112.9975 110.7862 112.3581
1991 114.8403 111.4232 98.4799 95.5409
[ reached getOption("max.print") -- omitted 5 rows ]plot(ajuste) # grafico da serie ajustada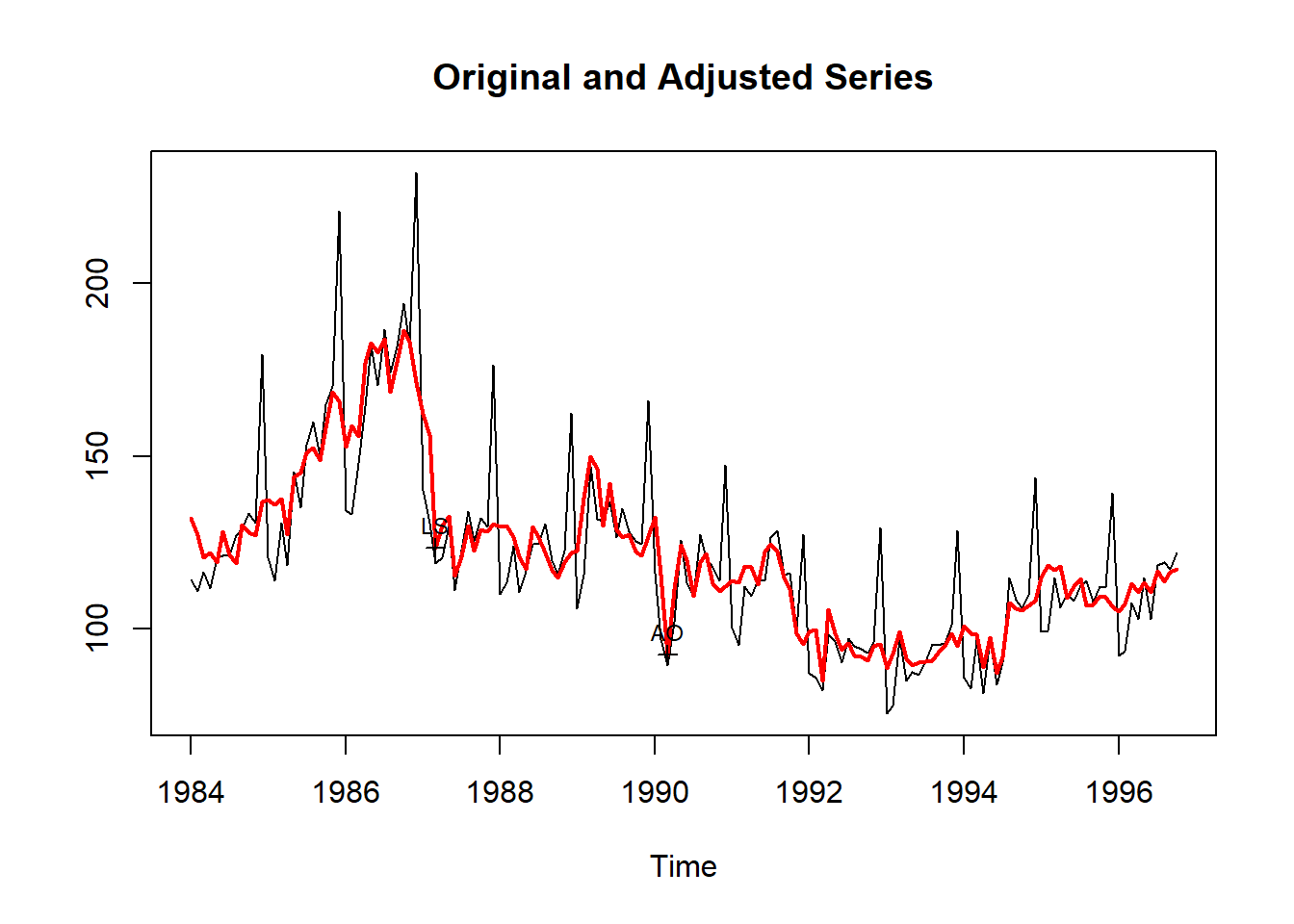
static(ajuste) # permite o ajuste manual do seasseas(x = consumo.ts, regression.variables = c("td1coef", "ls1987.Mar",
"ao1990.Mar"), arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")O static mostra o que foi feito e facilita a alteração de algum item específico, permitindo a replicação ou aperfeiçoamento (ajuste fino).
Replicando o automático
Replicando o modelo ‘automático’ a partir do resultado de static.
ajuste4 <- seas(x = consumo.ts, regression.variables = c("td1coef", "ls1988.Mar",
"ao1990.Mar"), arima.model = "(1 0 1)(1 0 0)", regression.aictest = NULL, outlier = NULL,
transform.function = "log")
summary(ajuste4)
Call:
seas(x = consumo.ts, transform.function = "log", regression.aictest = NULL,
outlier = NULL, regression.variables = c("td1coef", "ls1988.Mar",
"ao1990.Mar"), arima.model = "(1 0 1)(1 0 0)")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Weekday 0.00289 0.00180 1.61 0.11
LS1988.Mar 0.02855 0.06184 0.46 0.64
AO1990.Mar -0.30026 0.05529 -5.43 5.6e-08 ***
AR-Nonseasonal-01 0.99840 0.00241 413.87 < 2e-16 ***
AR-Seasonal-12 0.80449 0.04398 18.29 < 2e-16 ***
MA-Nonseasonal-01 0.37522 0.07160 5.24 1.6e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (1 0 1)(1 0 0) Obs.: 154 Transform: log
AICc: 1.18e+03, BIC: 1.21e+03 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 31 Shapiro (normality): 0.983 .
Messages generated by X-13:
Notes:
- Model used for SEATS decomposition is different from the model
estimated in the regARIMA modeling module of X-13ARIMA-SEATS.# seas(x = consumo.ts, regression.variables = c('td1coef', 'ls1987.Mar',
# 'ao1990.Mar'), arima.model = '(0 1 1)(0 1 1)', regression.aictest = NULL,
# outlier = NULL, transform.function = 'log')
# reproduzindo o codigo que saiu do static()
(seas(x = consumo.ts, regression.variables = c("td1coef", "ls1987.Mar", "ao1990.Mar"),
arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL, outlier = NULL, transform.function = "log"))
Call:
seas(x = consumo.ts, transform.function = "log", regression.aictest = NULL,
outlier = NULL, regression.variables = c("td1coef", "ls1987.Mar",
"ao1990.Mar"), arima.model = "(0 1 1)(0 1 1)")
Coefficients:
Weekday LS1987.Mar AO1990.Mar MA-Nonseasonal-01
0.00466 -0.24369 -0.23999 0.34580
MA-Seasonal-12
0.99996 # ajuste.auto<-view(ajuste4)Forecasts do ajuste
ajuste.fcst <- series(ajuste, c("forecast.forecasts"))
plot(ajuste.fcst)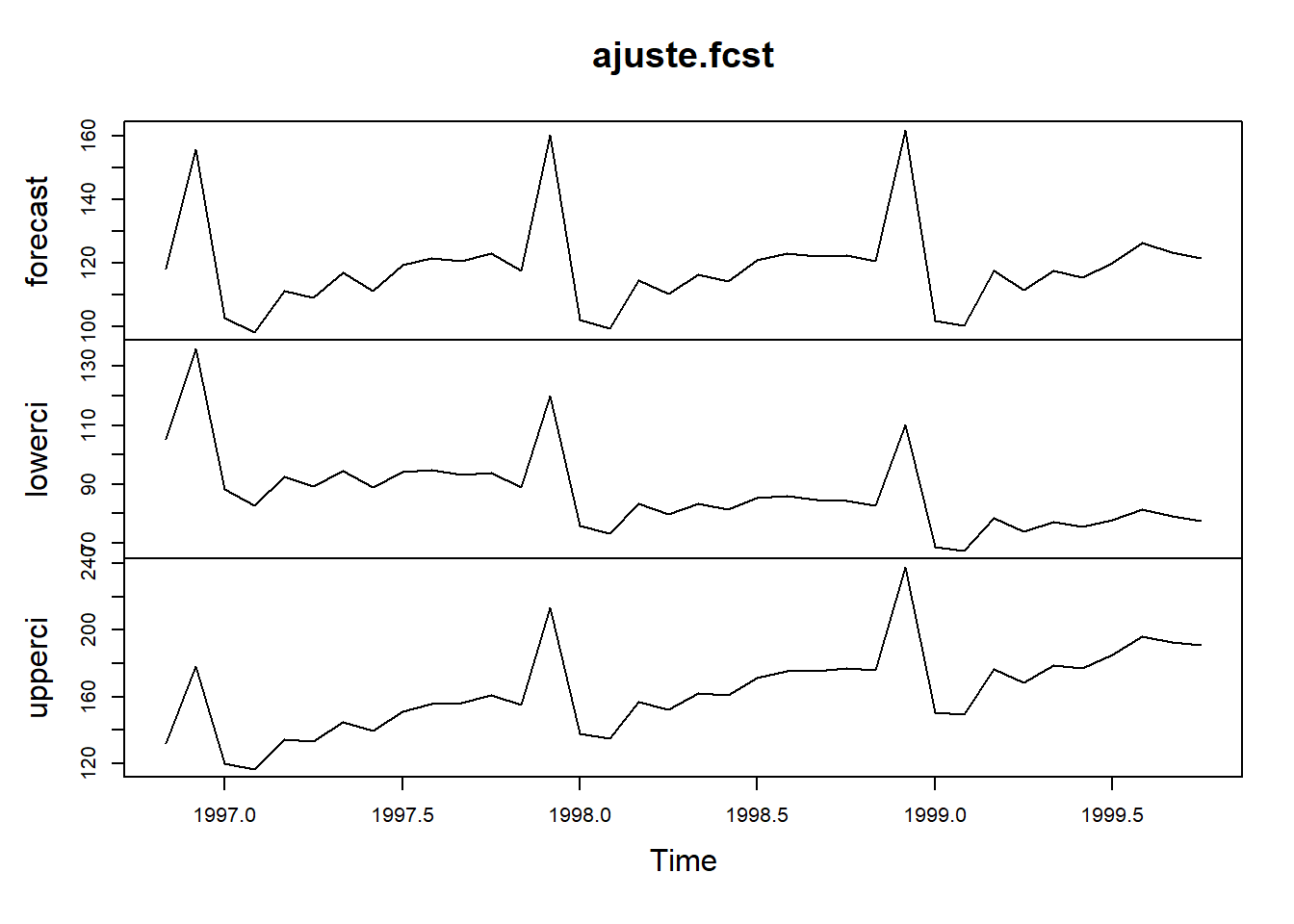
Correção do ajuste automático para o Calendário Brasileiro
Faremos a rotina como em Ferreira e Mato (2017). Obtemos os arquivos eletronicamente e colocamos no diretório de trabalho do projeto. Desta forma, conseguimos rodar mesmo sem internet.
# construção dias úteis (building working days) du <- read.csv2('dias_uteis.csv')
# head(du)
library(RCurl)
usingR_url_wd <- getURL("https://raw.githubusercontent.com/pedrocostaferreira/Articles/master/using-R-to-teach-seasonal-adjustment/work_days.csv")
wd <- read.csv2(text = usingR_url_wd)
head(wd) date Workdays days not_Workdays Workdays_ok.
1 jan/70 21 31 10 -4.0
2 fev/70 19 28 9 -3.5
3 mar/70 21 31 10 -4.0
4 abr/70 21 30 9 -1.5
5 mai/70 19 31 12 -11.0
6 jun/70 22 30 8 2.0# outra opcao é pegar direto do arquivo csv, dentro desta pasta uteis <-
# ts(du[,5], start = c(1970,1), freq = 12)
Workdays_ok <- ts(wd[, 5], start = c(1970, 1), freq = 12)
# building moving holidays (mh) feriados moveis construção feriados feriados <-
# read.csv2('feriados_moveis.csv') head(feriados)
usingR_url_mh <- getURL("https://raw.githubusercontent.com/pedrocostaferreira/Articles/master/using-R-to-teach-seasonal-adjustment/moving_holidays.csv")
mh <- read.csv2(text = usingR_url_mh)
# outra opcao é pegar direto do arquivo csv, dentro desta pasta
head(mh) # Pascoa e Carnaval Year Easter Carnival
1 1951 25/03/1951 06/02/1951
2 1952 13/04/1952 26/02/1952
3 1953 05/04/1953 17/02/1953
4 1954 18/04/1954 02/03/1954
5 1955 10/04/1955 22/02/1955
6 1956 01/04/1956 14/02/1956# Easter Pascoa (DOMINGO)
dates.easter <- as.Date(as.character(mh$Easter), "%d/%m/%Y")
easter <- genhol(dates.easter, start = -8, end = 1, frequency = 12)
# Carnival (TERCA-FEIRA DE CARNAVAL)
dates.carnival <- as.Date(as.character(mh$Carnival), "%d/%m/%Y")
carnival <- genhol(dates.carnival, start = -3, end = 1, frequency = 12, center = "calendar")
# carnival <- genhol(dates.carnival, start = -3, end = 1, frequency = 12)
regs <- na.omit(cbind(Workdays_ok, easter, carnival))
regs2 <- na.omit(cbind(Workdays_ok, carnival))
head(regs) Workdays_ok easter carnival
Jan 1970 -4.0 0 0.000000
Feb 1970 -3.5 0 0.203125
Mar 1970 -4.0 1 -0.203125
Apr 1970 -1.5 0 0.000000
May 1970 -11.0 0 0.000000
Jun 1970 2.0 0 0.000000head(regs2) Workdays_ok carnival
Jan 1970 -4.0 0.000000
Feb 1970 -3.5 0.203125
Mar 1970 -4.0 -0.203125
Apr 1970 -1.5 0.000000
May 1970 -11.0 0.000000
Jun 1970 2.0 0.000000options(digits = 6)Modelo com ajuste do calendário brasileiro
ajuste2 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL, regression.usertype = "holiday",
forecast.save = "forecasts")
### COLOCAR NATAL E OUTROS FERIADOS IMPORTANTES PARA MODELAR O VAREJO
# ajuste2 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
# regression.usertype = c('td', 'easter', 'holiday'))
options(digits = 6)
# view(ajuste2)
qs(ajuste2) qs p-val
qsori 198.629 0
qsorievadj 207.667 0
qsrsd 0.000 1
qssadj 0.000 1
qssadjevadj 0.000 1
qsirr 0.000 1
qsirrevadj 0.000 1
qssori 103.976 0
qssorievadj 115.581 0
qssrsd 0.000 1
qsssadj 0.000 1
qsssadjevadj 0.000 1
qssirr 0.000 1
qssirrevadj 0.000 1summary(ajuste2)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
xreg1 0.00470 0.00109 4.32 1.6e-05 ***
xreg2 0.00223 0.02097 0.11 0.9155
xreg3 -0.07330 0.02276 -3.22 0.0013 **
AO1990.Mar -0.24401 0.04934 -4.95 7.6e-07 ***
MA-Nonseasonal-01 0.22298 0.07350 3.03 0.0024 **
MA-Seasonal-12 0.99995 0.06489 15.41 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 154 Transform: log
AICc: 986, BIC: 1.01e+03 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 26.5 Shapiro (normality): 0.987 ajuste2a <- seas(x = consumo.ts, xreg = regs2, regression.aictest = NULL, regression.usertype = "holiday",
forecast.save = "forecasts")
summary(ajuste2a)
Call:
seas(x = consumo.ts, xreg = regs2, regression.aictest = NULL,
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
xreg1 0.00468 0.00107 4.36 1.3e-05 ***
xreg2 -0.07421 0.02110 -3.52 0.00044 ***
AO1990.Mar -0.24545 0.04748 -5.17 2.4e-07 ***
MA-Nonseasonal-01 0.22314 0.07349 3.04 0.00240 **
MA-Seasonal-12 0.99995 0.06487 15.41 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 154 Transform: log
AICc: 984, BIC: 1e+03 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 26.6 Shapiro (normality): 0.988 static(ajuste2a)seas(x = consumo.ts, xreg = regs2, regression.usertype = "holiday",
forecast.save = "forecasts", regression.variables = "ao1990.Mar",
arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")# ACURACIA
library(Metrics)
# mae(actual, predicted) rmse(actual, predicted)
predicted <- final(ajuste2a)
actual <- consumo.ts
(mae2 <- mae(actual, predicted))[1] 9.52081(rmse2 <- rmse(actual, predicted))[1] 14.5961# ajuste conforme o auto.arima da semana passada
ajuste3 <- seas(x = consumo.ts, xreg = regs2, regression.usertype = "holiday", forecast.save = "forecasts",
regression.variables = "ao1990.Mar", arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")
summary(ajuste3)
Call:
seas(x = consumo.ts, xreg = regs2, transform.function = "log",
regression.aictest = NULL, outlier = NULL, regression.usertype = "holiday",
forecast.save = "forecasts", regression.variables = "ao1990.Mar",
arima.model = "(0 1 1)(0 1 1)")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO1990.Mar -0.24545 0.04748 -5.17 2.4e-07 ***
xreg1 0.00468 0.00107 4.36 1.3e-05 ***
xreg2 -0.07421 0.02110 -3.52 0.00044 ***
MA-Nonseasonal-01 0.22314 0.07349 3.04 0.00240 **
MA-Seasonal-12 0.99996 0.06487 15.41 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 154 Transform: log
AICc: 984, BIC: 1e+03 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 26.6 Shapiro (normality): 0.988 predicted3 <- final(ajuste3)
actual <- consumo.ts
(mae3 <- mae(actual, predicted3))[1] 9.52081(rmse3 <- rmse(actual, predicted3))[1] 14.5961# melhor ficar como estava no ajuste2a
# figura dos fatores sazonais
monthplot(ajuste3, col.base = 1)
legend("topleft", legend = c("Irregular", "Seasonal", "Seasonal Average"), col = c(4,
2, 1), lwd = c(1, 2, 2), lty = 1, bty = "n", cex = 0.6)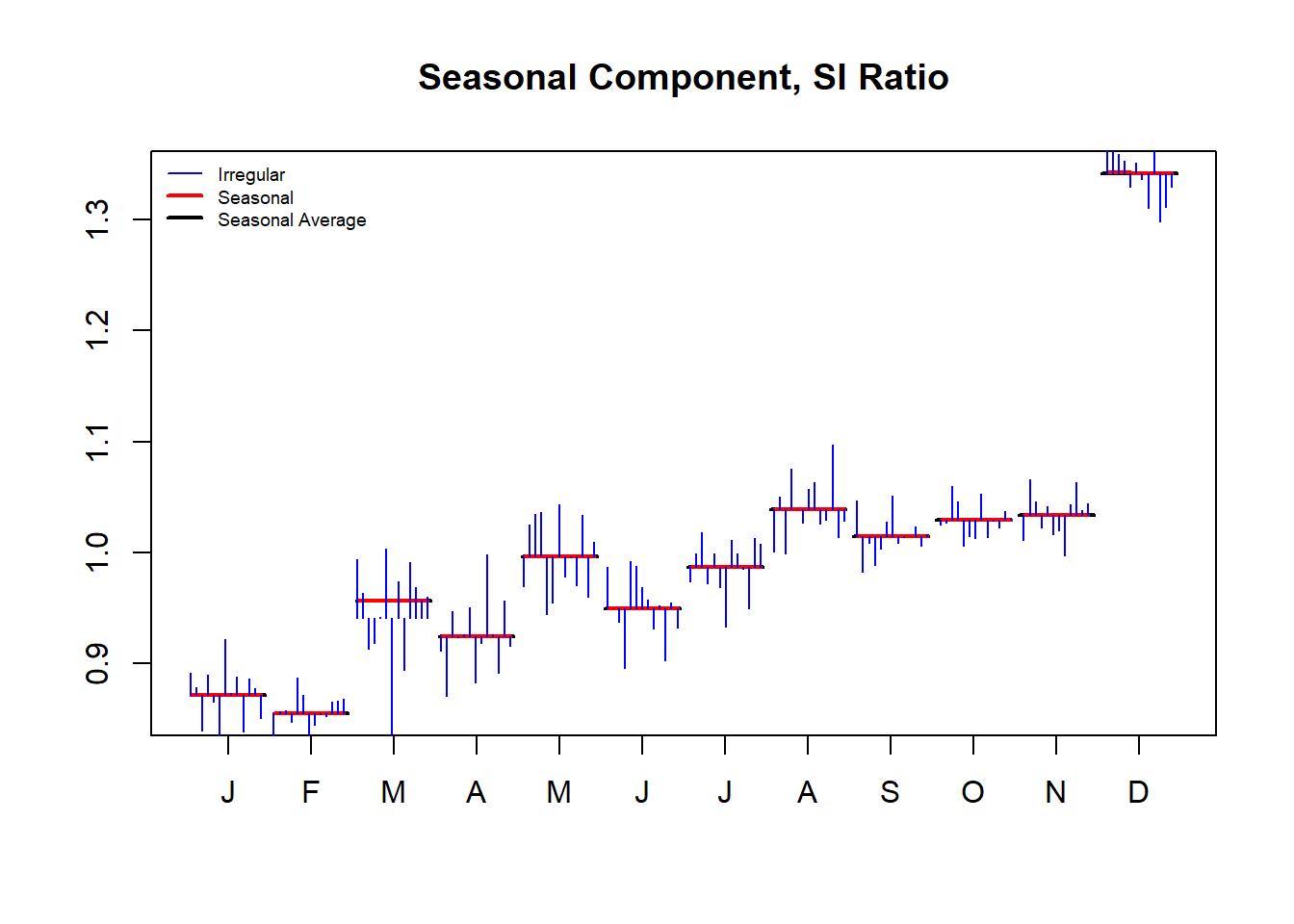
# figura da série ajustada
plot(ajuste3, main = "Ajuste 3 de consumo.ts")
grid()
legend("topleft", legend = c("Original", "Adjusted"), col = c(1, 2), lwd = c(1, 2),
lty = 1, bty = "n", cex = 0.6)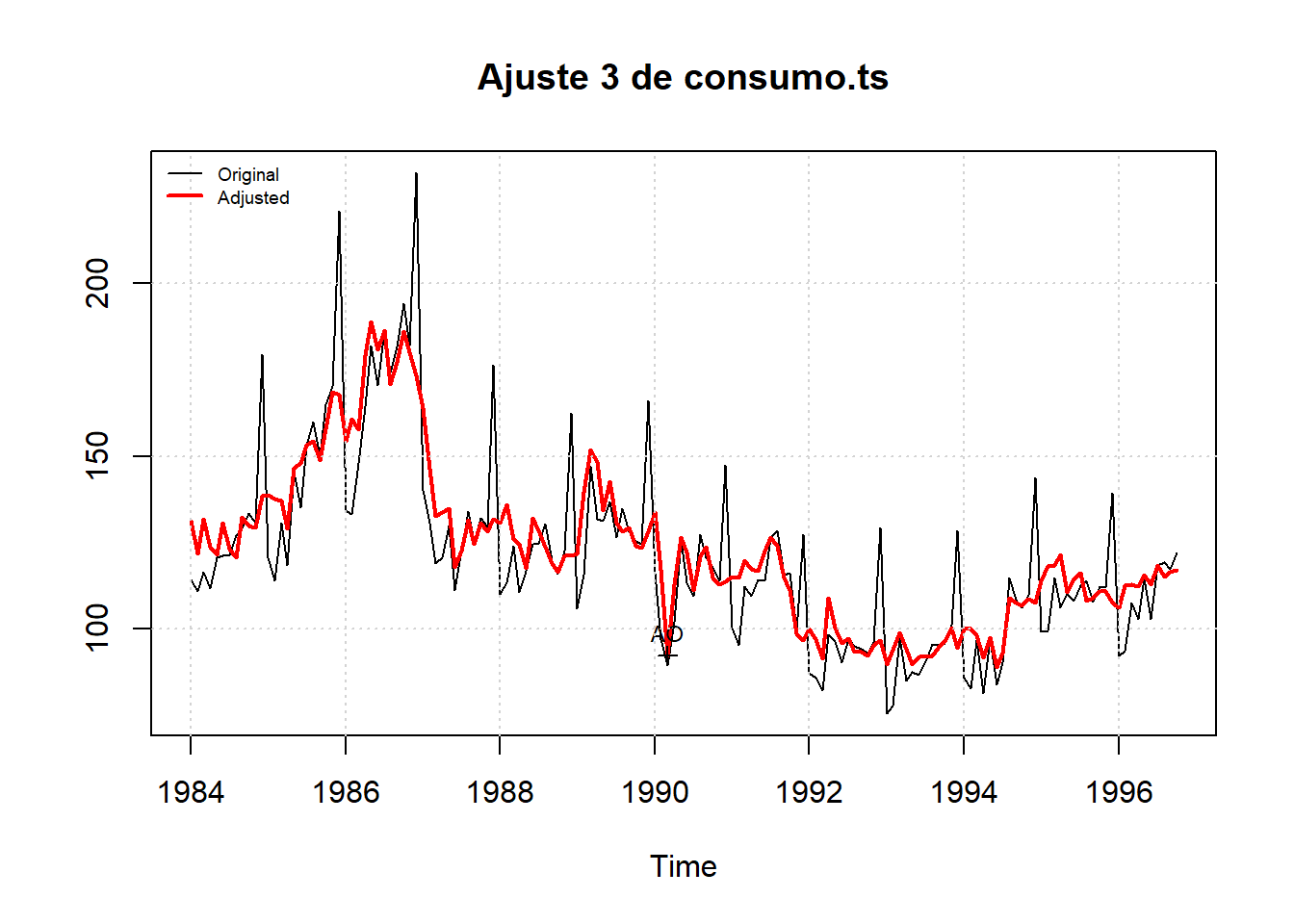
# forecasts do ajuste3 o mesmo que ajuste3$series$fct
forecasts3 <- series(ajuste3, c("forecast.forecasts"))
require(graphics)
require(zoo)
data.fcst <- cbind.zoo(consumo.ts, series(ajuste3, "forecast.forecasts"))
ts.plot(data.fcst, col = c(1, 2, 3, 4), main = "série original de consumo e forecasts ajuste3",
xlab = "Mês/Ano")
legend("bottomleft", lty = 1, pch = 1, col = 1:4, c("data", "X13as", "Lim Inferior",
"Lim Superior"))
grid()
# opcao grafica
library(dygraphs)
dygraph(data.fcst)dygraph(data.fcst, main = "Indice de consumo do varejo de São Paulo,
Moretin e Toloi (2005)") %>%
dyAxis("y", label = "Indice", valueRange = c(55, 250), axisLabelFontSize = 20) %>%
dyAxis("x", label = "Mês/Ano", axisLabelFontSize = 20) %>% dyGroup(c("consumo",
"forecast"), drawPoints = TRUE, color = c("blue", "red")) %>% dyLegend(width = 400) %>%
dyAnnotation("1990-3-1", text = "AO-mar1990", attachAtBottom = TRUE, width = 100) %>%
dyOptions(drawPoints = TRUE, pointSize = 5, pointShape = "triangle", axisLineWidth = 1.5)Referências
FERREIRA, Pedro Costa; SPERANZA, Talitha; COSTA, Jonatha (2018). BETS: Brazilian Economic Time Series. R package version 0.4.9. Disponível em: https://CRAN.R-project.org/package=BETS.
FERREIRA, Pedro C.; MATOS, Daiane M. Usando o R para ensinar Ajuste Sazonal. São Paulo: FGV, 2017. 18p. Disponível em: http://portalibre.fgv.br/lumis/portal/file/fileDownload.jsp?fileId=8A7C82C5519A547801533DF7BE5E2D0D
HYNDMAN, Rob. (2018). fpp2: Data for “Forecasting: Principles and Practice” (2nd Edition). R package version 2.3. Disponível em: https://CRAN.R-project.org/package=fpp2.
HYNDMAN, R.J., & ATHANASOPOULOS, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. Disponível em: https://otexts.com/fpp2/. Accessed on 12 Set 2019.
MORETTIN, Pedro A.; TOLOI, Clélia M.C. Análise de Séries Temporais. São paulo: Editora Edgard Blücher, 2004. https://www.ime.usp.br/~pam/st/