Séries Temporais com R: Combinação de forecasts para o Consumo do Varejo em MS com `forecastHybrid`

Last updated on Apr 27, 2020 10 min read

Licença

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0

Citação

Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Séries Temporais com R: Combinação de forecasts para o Consumo do Varejo em MS com forecastHybrid. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/forecastHybrid_varejoms e em https://adrianofigueiredo.netlify.app/post/series-temporais-combinacao-de-forecasts-forecasthybrid/.

Script para reprodução (se utilizar, citar como acima)

Download 2020-04-27-séries-temporais-combinação-de-forecasts-forecasthybrid.Rmd

Introdução

Neste arquivo utilizo a série do Índice de volume de vendas no varejo Total de Mato Grosso do Sul, série mensal a partir de jan/2000 até jul/2019 obtida com o pacote BETS e importada do Banco Central do Brasil. Portanto, são 235 observações mensais.

Dados

Farei de duas formas para o leitor. Uma carrega direto do site do Banco Central do Brasil com o pacote BETS (FERREIRA, SPERANZA e COSTA, 2018) e a outra eu gerei a estrutura idêntica pela função dput() para os leitores que não conseguirem por qualquer motivo o acesso ao site do Banco Central (as vezes vejo isso ocorrer dependendo dos bloqueios da sua rede de internet). A forma pelo dput assume o nome varejoms2 enquanto a extraída pelo BETS tem nome varejoms. Esclareço ao leitor que após baixar a série pelo BETS, fiz o dput e a partir de então, desabilitei o bloco (Chunk) que acessa o BETS apenas para agilizar os cálculos.

library(BETS)
# Pegando as séries a partir do site do Banco Central do Brasil
# Índice de volume de vendas no varejo Total de Mato Grosso do Sul
# mensal a partir de jan/2000 até jul/2019 
# 235 observações mensais
varejoms <- BETSget(1479) 
print(varejoms)
class(varejoms)
dput(varejoms)  # opção para ter os dados como na structure abaixo

library(BETS)

# Pegando as séries a partir do site do Banco Central do Brasil Índice de volume
# de vendas no varejo Total de Mato Grosso do Sul mensal a partir de jan/2000 até
# jul/2019 (em 04.10.2019)

# varejoms <- BETSget(1479)

varejoms <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6, 
    35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3, 
    36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6, 
    35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3, 
    43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3, 
    47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5, 
    47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6, 
    55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7, 
    77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1, 
    64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5, 
    64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7, 
    82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5, 
    88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4, 
    101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6, 
    93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4, 
    90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5, 
    93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5, 
    96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 90.9), .Tsp = c(2000, 2019.5, 
    12), class = "ts")

A rotina de dados obtidos pelo BETS já retorna a série em formato ts, ou seja, série temporal. Farei então a criação de uma série em diferenças para observar o comportamento da série em nível e em diferenças.

Inicialmente olharei as estatísticas descritivas da série. Em seguida farei um plot básico da série e o plot pelo pacote dygraphs, útil para ver os pontos de picos e momentos específicos.

dvarejo <- diff(varejoms)
# estatisticas basicas
summary(varejoms)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  31.60   44.05   64.50   67.28   90.00  129.60

# Min. 1st Qu.  Median Mean 3rd Qu.  Max.  31.60 44.05 64.50 67.28 90.00 129.60

# plot basico lembrar que em class(), ele já indicou que era ts = serie temporal
plot(varejoms)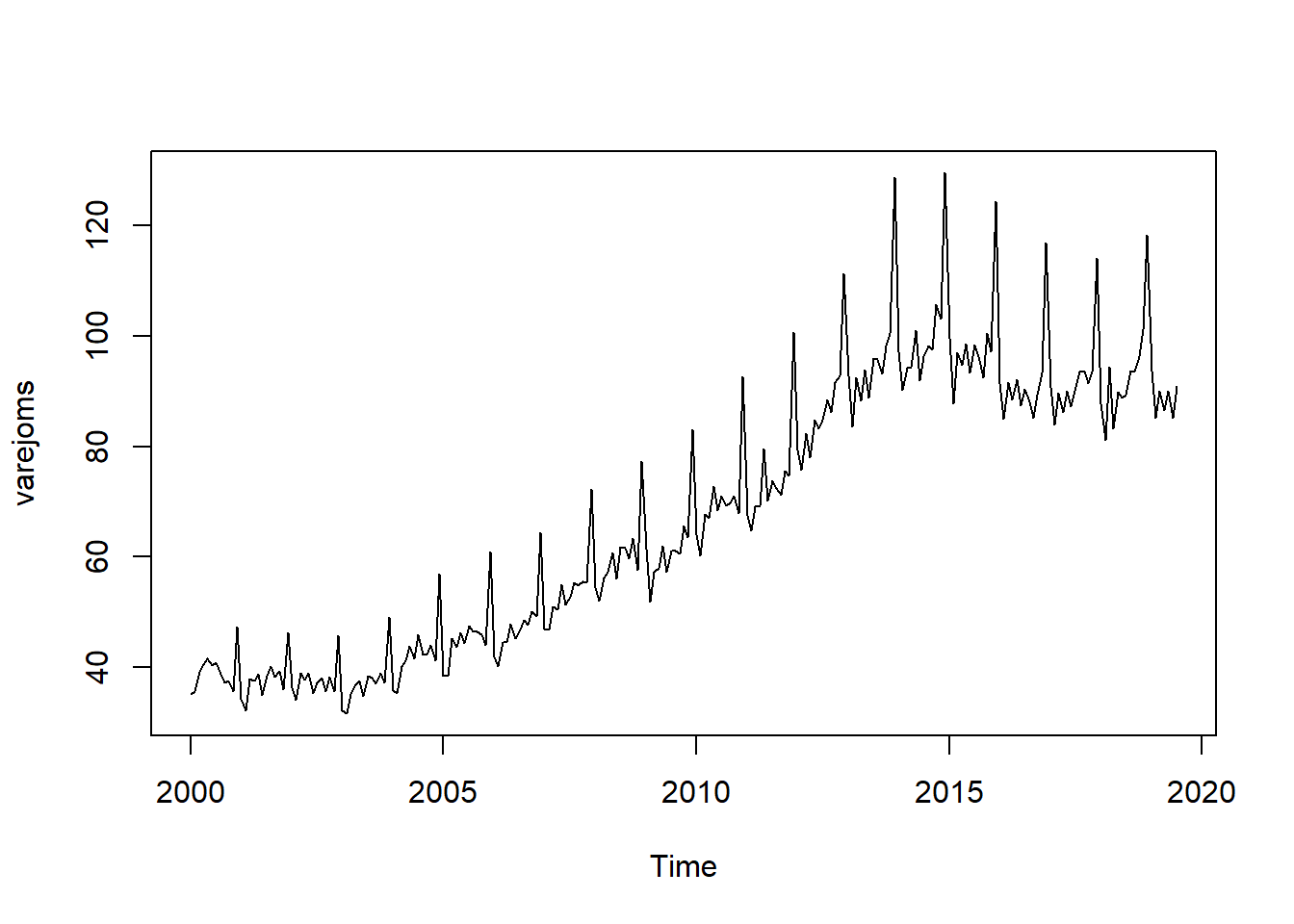

# pelo pacote dygraph dá mais opções
library(dygraphs)
dygraph(varejoms, main = "Índice de volume de vendas no varejo total de Mato Grosso do Sul <br> (Mensal)  (2011=100) BCB 1479") %>% 
    dyAxis("x", drawGrid = TRUE) %>% dyEvent("2005-1-01", "2005", labelLoc = "bottom") %>% 
    dyEvent("2015-1-01", "2015", labelLoc = "bottom") %>% dyEvent("2018-1-01", "2018", 
    labelLoc = "bottom") %>% dyEvent("2019-1-01", "2019", labelLoc = "bottom") %>% 
    dyOptions(drawPoints = TRUE, pointSize = 2)

É possivel visualizar nos plots acima: sazonalidade (por exemplo, picos em dezembro de cada ano); a tendência aparentemente crescente até 2014 e decresce com a “crise” brasileira; e uma aparente não-estacionariedade (média e variância mudam no tempo).

Análise da série

Uma ressalva deve ser feita, que no presente exercício, não farei a divisão entre amostra teste e amostra treino, de modo que usarei a série toda para os ajustes. O leitor deve em geral fazer estas divisões para certificar de que o modelo é um bom preditor.

Farei a estimação para o modelo rápido usando o forecastHybrid de Shaub e Ellis (2019). Portanto, especificarei a série de varejoms, sem me preocupar de início com a sazonalidade e a não-estacionariedade da série, imaginando que os modelos conseguirão resolver essa situação.

Aplicação do `forecastHybrid`

O modelo combina os métodos: ARIMA (Auto Regressive Integrated Moving Average), o ETS (Error Trend Seasonal de decomposição espaço estado), o NNETAR (Neural Network Autoregressive), o STLM (Seasonal and Trend decomposition using Loess), o Thetam (método Theta de Assimakopoulos e Nikolopoulos, 2000), o TBATS (Exponential Smoothing Method + Box-Cox Transformation + ARMA model for residuals + Trigonometric Seasonal).

A função hybridModel utiliza a opção models para indicar quais os modelos a serem utilizados.

set.seed(12345)
library(forecastHybrid)
library(forecast)
library(fpp2)
library(zoo)
quickModel <- hybridModel(varejoms)
# estima os modelos: auto.arima, ets, thetam, nnetar, stlm e tbats
fcst.res <- forecast(quickModel, h = 60, PI.combination = c("mean"))
class(quickModel)

[1] "hybridModel"

print(quickModel)

Hybrid forecast model comprised of the following models: auto.arima, ets, thetam, nnetar, stlm, tbats
############
auto.arima with weight 0.167 
############
ets with weight 0.167 
############
thetam with weight 0.167 
############
nnetar with weight 0.167 
############
stlm with weight 0.167 
############
tbats with weight 0.167

accuracy(quickModel)

                 ME     RMSE      MAE         MPE    MAPE       ACF1 Theil's U
Test set 0.06663916 2.510118 1.881037 -0.03385045 2.69985 0.08673647 0.2780059

autoplot(varejoms) + autolayer(fcst.res$mean, series = "Combinação") + xlab("Ano") + 
    ylab("Índice (2011=100)") + ggtitle("Varejo MS: Forecast híbrido 
     considerando modelos SARIMA, ETS, Thetam, NNETAR, STLM e TBATS: 
     Período Ago/2019-Julho/2024")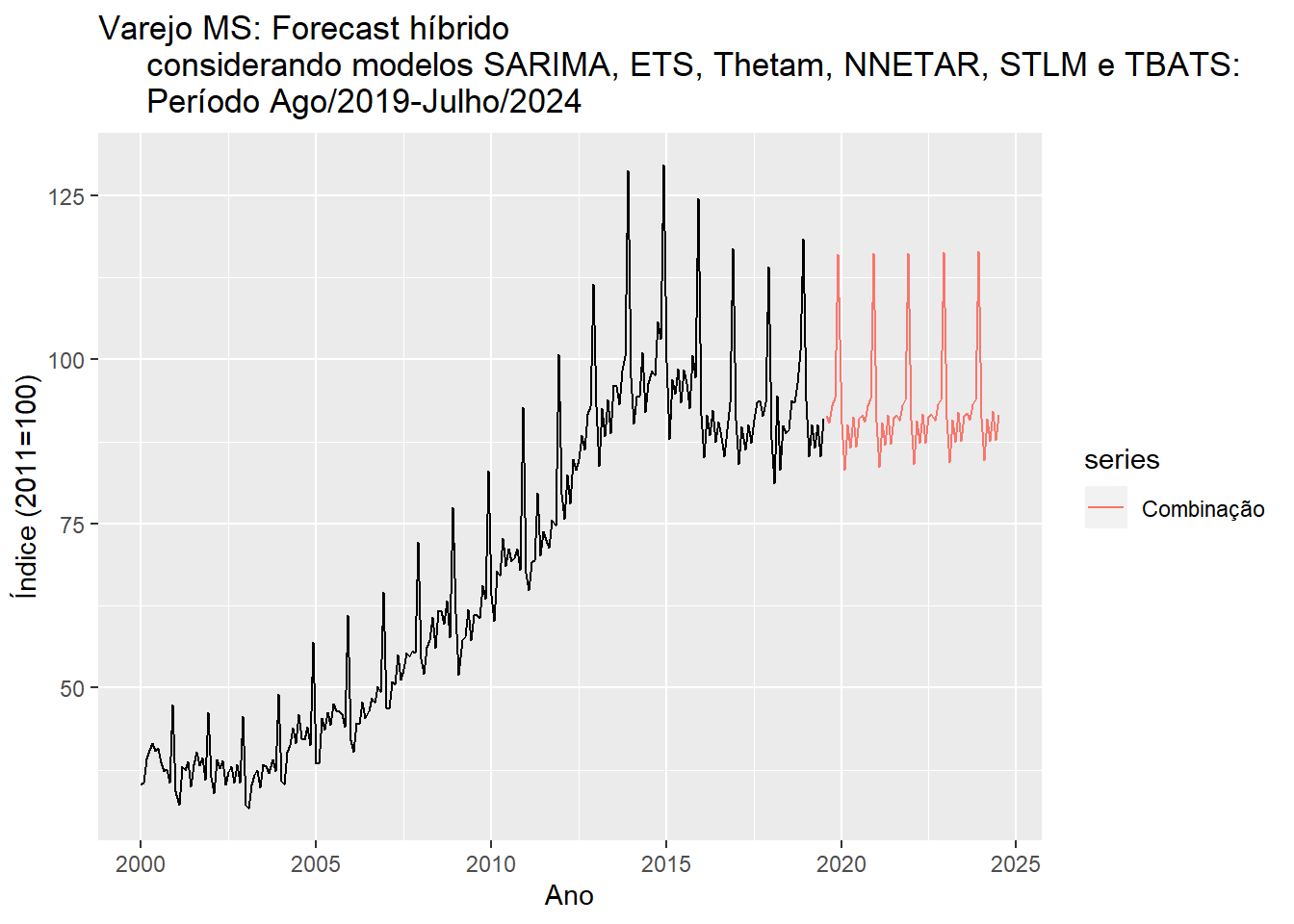

matriz.res <- cbind(varejoms, fcst.res$mean, ts(fcst.res$lower[, 2], start = c(2019, 
    3), frequency = 12), ts(fcst.res$upper[, 2], start = c(2019, 3), frequency = 12))
writexl::write_xlsx(as.data.frame(matriz.res), "resid.xlsx")
autoplot(varejoms) + autolayer(matriz.res[, 2], series = "Combinação") + autolayer(matriz.res[, 
    3], series = "PI inferior 95%") + autolayer(matriz.res[, 4], series = "PI superior 95%") + 
    xlab("Ano") + ylab("Índice (2011=100)") + ggtitle("Varejo MS: Forecast híbrido 
     considerando modelos SARIMA, ETS, Thetam, NNETAR, STLM e TBATS: 
     Período Ago/2019-Julho/2024")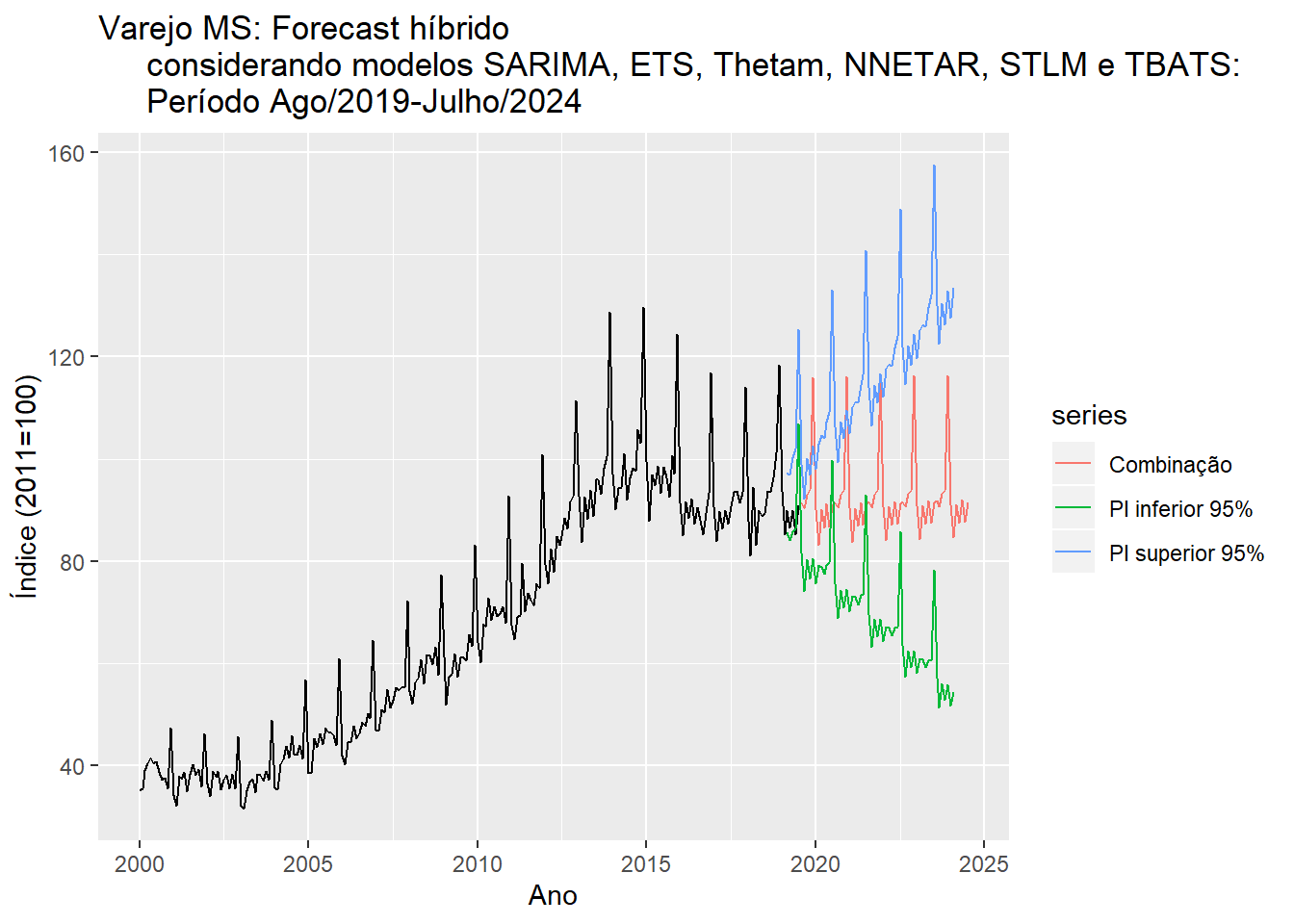

Vamos aperfeiçoar o modelo ARIMA para permitir mais defasagens que o padrão.

#### OPCAO PELOS PESOS IGUAIS
set.seed(12345)
hmi <- hybridModel(y = varejoms, models = "aefnstz", a.args = list(stepwise = FALSE, 
    approximation = FALSE))
(acuraciai <- accuracy(hmi, individual = TRUE))

$auto.arima
                      ME     RMSE      MAE        MPE     MAPE      MASE
Training set 0.009480306 2.384598 1.779725 0.02458176 2.619097 0.3883732
                    ACF1
Training set 0.004907171

$ets
                      ME     RMSE      MAE     MPE     MAPE      MASE
Training set -0.07940018 2.328173 1.771169 -0.1044 2.656467 0.3865061
                   ACF1
Training set 0.01989582

$thetam
                    ME     RMSE      MAE        MPE     MAPE      MASE
Training set 0.2933461 6.536434 3.911442 -0.2496862 5.539406 0.8535586
                      ACF1
Training set -0.0008177642

$nnetar
                      ME     RMSE      MAE        MPE     MAPE      MASE
Training set 0.003079752 3.808572 2.940988 -0.3362463 4.378705 0.6417852
                  ACF1
Training set 0.5553674

$stlm
                      ME     RMSE      MAE        MPE     MAPE      MASE
Training set -0.01530687 2.022176 1.569836 0.06511203 2.413031 0.3425711
                   ACF1
Training set -0.0037393

$tbats
                     ME     RMSE      MAE       MPE  MAPE      MASE       ACF1
Training set 0.07622443 2.435786 1.930459 0.1243821 2.971 0.3230086 0.02305048

$snaive
                   ME     RMSE      MAE      MPE     MAPE MASE      ACF1
Training set 2.936771 5.817096 4.582511 4.332151 6.778317    1 0.8135737

Separando algumas medidas de acurácia de interesse.

RMSE = c(ETS = acuraciai$ets[, "RMSE"], ARIMA = acuraciai$auto.arima[, "RMSE"], `STL-ETS` = acuraciai$stlm[, 
    "RMSE"], NNAR = acuraciai$nnetar[, "RMSE"], TBATS = acuraciai$tbats[, "RMSE"], 
    THETA = acuraciai$thetam[, "RMSE"], SNAIVE = acuraciai$snaive[, "RMSE"], Combinacao = accuracy(hmi)[, 
        "RMSE"])

MAPE = c(ETS = acuraciai$ets[, "MAPE"], ARIMA = acuraciai$auto.arima[, "MAPE"], `STL-ETS` = acuraciai$stlm[, 
    "MAPE"], NNAR = acuraciai$nnetar[, "MAPE"], TBATS = acuraciai$tbats[, "MAPE"], 
    THETA = acuraciai$thetam[, "MAPE"], SNAIVE = acuraciai$snaive[, "MAPE"], Combinacao = accuracy(hmi)[, 
        "MAPE"])

MAE = c(ETS = acuraciai$ets[, "MAE"], ARIMA = acuraciai$auto.arima[, "MAE"], `STL-ETS` = acuraciai$stlm[, 
    "MAE"], NNAR = acuraciai$nnetar[, "MAE"], TBATS = acuraciai$tbats[, "MAE"], THETA = acuraciai$thetam[, 
    "MAE"], SNAIVE = acuraciai$snaive[, "MAE"], Combinacao = accuracy(hmi)[, "MAE"])

tabelai <- cbind(RMSE, MAE, MAPE)
knitr::kable(tabelai)

	RMSE	MAE	MAPE
ETS	2.328173	1.771168	2.656467
ARIMA	2.384598	1.779724	2.619097
STL-ETS	2.022176	1.569836	2.413031
NNAR	3.864074	2.965666	4.395012
TBATS	2.435786	1.930459	2.971000
THETA	6.536434	3.911442	5.539406
SNAIVE	5.817096	4.582511	6.778316
Combinacao	2.637798	1.979749	2.850239

# estima os modelos: auto.arima, ets, thetam, nnetar, stlm, tbats e snaive
fcst.resi <- forecast(hmi, h = 12, PI.combination = c("mean"))
class(hmi)

[1] "hybridModel"

print(hmi)

Hybrid forecast model comprised of the following models: auto.arima, ets, thetam, nnetar, stlm, tbats, snaive
############
auto.arima with weight 0.143 
############
ets with weight 0.143 
############
thetam with weight 0.143 
############
nnetar with weight 0.143 
############
stlm with weight 0.143 
############
tbats with weight 0.143 
############
snaive with weight 0.143

accuracy(hmi)

               ME     RMSE      MAE       MPE     MAPE      ACF1 Theil's U
Test set 0.475493 2.637798 1.979749 0.5901505 2.850239 0.2312181  0.294658

Comparação com dados novos

Agora que já temos as informações até fev/2020, podemos comparar as estimativas com os dados reais. Faremos a comparação relativamente ao forecast do forecast::thetaf.

# dadosnovos<-BETS::BETSget(1479)
dadosnovos <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6, 
    35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3, 
    36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6, 
    35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3, 
    43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3, 
    47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5, 
    47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6, 
    55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7, 
    77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1, 
    64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5, 
    64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7, 
    82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5, 
    88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4, 
    101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6, 
    93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4, 
    90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5, 
    93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5, 
    96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 91, 94.4, 93.4, 95.9, 102.6, 
    116, 94.9, 89.1), .Tsp = c(2000, 2020.08333333333, 12), class = "ts")
# View(cbind.zoo(data.fcst,dadosnovos))
require(zoo)
print(cbind.zoo(fcst.resi$mean, dadosnovos)[236:242])

         fcst.resi$mean dadosnovos
ago 2019       91.67066       94.4
set 2019       90.90770       93.4
out 2019       93.57165       95.9
nov 2019       95.12952      102.6
dez 2019      116.17440      116.0
jan 2020       90.70896       94.9
fev 2020       83.44558       89.1

Acurácia do período Agosto/2019 a fev/2020:

previstoi <- fcst.resi$mean
observadoi <- dadosnovos[236:242]
forecast::accuracy(previstoi, observadoi)

               ME     RMSE      MAE      MPE     MAPE
Test set 3.527361 4.216596 3.577189 3.697257 3.740212

Ou seja, um erro percentual médio de \(\approx3.7\)% e um erro absoluto médio de \(\approx3.74\)%, portanto, inferior às estimativas feitas pelo método Theta (https://rpubs.com/amrofi/varejoms_thetaf). Talvez ganhemos algo pelo X13ARIMA-SEATS (https://rpubs.com/amrofi/x13arima_seats_varejoms) ao inseri-lo na combinação. Fica para outro exercício a simulação da combinação incluindo o X13ARIMA-SEATS.

Referências

ASSIMAKOPOULOS, V. and NIKOLOPOULOS, K. (2000). The theta model: a decomposition approach to forecasting. International Journal of Forecasting, 16, 521-530. DOI: https://doi.org/10.1016/S0169-2070(00)00066-2

FERREIRA, Pedro Costa; SPERANZA, Talitha; COSTA, Jonatha (2018). BETS: Brazilian Economic Time Series. R package version 0.4.9. Disponível em: https://CRAN.R-project.org/package=BETS.

HYNDMAN, Rob J. (2018a). fpp2: Data for “Forecasting: Principles and Practice” (2nd Edition). R package version 2.3. Disponível em: https://CRAN.R-project.org/package=fpp2.

HYNDMAN, Rob J. (2018b). A forecast ensemble benchmark. Disponível em:https://robjhyndman.com/hyndsight/benchmark-combination/.

HYNDMAN, R.J., & ATHANASOPOULOS, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. Disponível em: https://otexts.com/fpp2/. Accessed on 12 Set 2019.

SHAUB, David; ELLIS, Peter. (2019). forecastHybrid: Convenient Functions for Ensemble Time Series Forecasts. R package version 4.2.17. Disponível em: https://CRAN.R-project.org/package=forecastHybrid. Accessed on 27 Apr 2020.

Adriano M R Figueiredo

Professor of Regional Economics and Econometrics

My research interests include regional economics, econometrics, sustainable public policies and agricultural economics.