Séries Temporais com R: Análise ARIMA do Consumo do Varejo em MS com X13ARIMA-SEATS
Licença
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0
Citação
Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Séries Temporais com R: Análise ARIMA do Consumo do Varejo em MS com X13ARIMA-SEATS. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/x13arima_seats_varejoms e em https://adrianofigueiredo.netlify.app/post/series-temporais-consumo-varejo-ms-x13arima-seats/.
Script para reprodução (se utilizar, citar como acima)
Download 2020-04-16-séries-temporais-consumo-varejo-ms-x13arima-seats.RmdIntrodução
Neste arquivo utilizo a série do Índice de volume de vendas no varejo Total de Mato Grosso do Sul, série mensal a partir de jan/2000 até jul/2019 obtida com o pacote BETS e importada do Banco Central do Brasil. Portanto, são 235 observações mensais.
Dados
Farei de duas formas para o leitor. Uma carrega direto do site do Banco Central do Brasil com o pacote BETS (FERREIRA, SPERANZA e COSTA, 2018) e a outra eu gerei a estrutura idêntica pela função dput() para os leitores que não conseguirem por qualquer motivo o acesso ao site do Banco Central (as vezes vejo isso ocorrer dependendo dos bloqueios da sua rede de internet). A forma pelo dput assume o nome varejoms2 enquanto a extraída pelo BETS tem nome varejoms. Esclareço ao leitor que após baixar a série pelo BETS, fiz o dput e a partir de então, desabilitei o bloco (Chunk) que acessa o BETS apenas para agilizar os cálculos.
library(BETS)
# Pegando as séries a partir do site do Banco Central do Brasil
# Índice de volume de vendas no varejo Total de Mato Grosso do Sul
# mensal a partir de jan/2000 até jul/2019
# 235 observações mensais
varejoms <- BETSget(1479)
print(varejoms)
class(varejoms)
dput(varejoms) # opção para ter os dados como na structure abaixosuppressMessages(library(fpp2))
suppressMessages(library(tseries))
suppressMessages(library(zoo))
suppressMessages(library(forecast))
suppressMessages(library(ggplot2))
# Pegando as séries a partir do site do Banco Central do Brasil Índice de volume
# de vendas no varejo Total de Mato Grosso do Sul mensal a partir de jan/2000 até
# jul/2019 Loading the dataset library(readxl) dados <-
# read_excel('dados.xlsx',sheet = 'dados') attach(dados) library(BETS)
# Pegando as séries a partir do site do Banco Central do Brasil Índice de volume
# de vendas no varejo Total de Mato Grosso do Sul mensal a partir de jan/2000 até
# jul/2019 (em 12.09.2019)
# varejoms <- BETSget(1479)
varejoms <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6,
35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3,
36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6,
35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3,
43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3,
47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5,
47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6,
55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7,
77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1,
64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5,
64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7,
82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5,
88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4,
101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6,
93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4,
90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5,
93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5,
96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 90.9), .Tsp = c(2000, 2019.5,
12), class = "ts")Modelo Census X13-ARIMA-SEATS
suppressMessages(library(seasonal)) #chamando o pacote
checkX13() #checagem se o x13 está operacional no RStudioRelembrando o gráfico da série
consumo.ts <- varejoms
plot(consumo.ts, xlab = "Tempo")
abline(h = seq(40, 230, 5), v = seq(2000, 2017, 1), lty = 3, col = "darkgrey")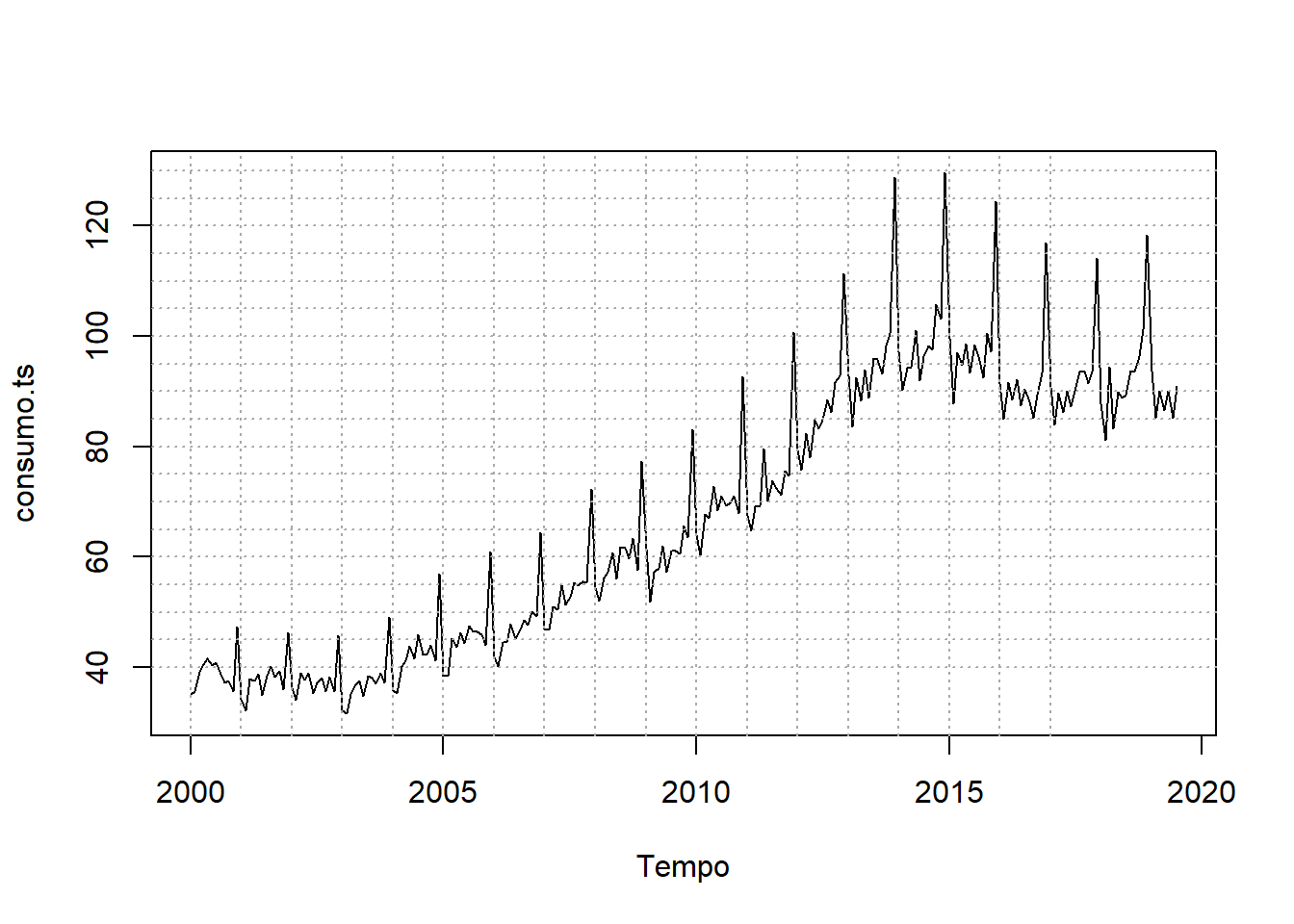
monthplot(consumo.ts, labels = month.abb, lty.base = 2)
legend("topleft", legend = c("consumo/mes", "media/mes"), cex = 0.8, lty = c(1, 2),
bty = "n")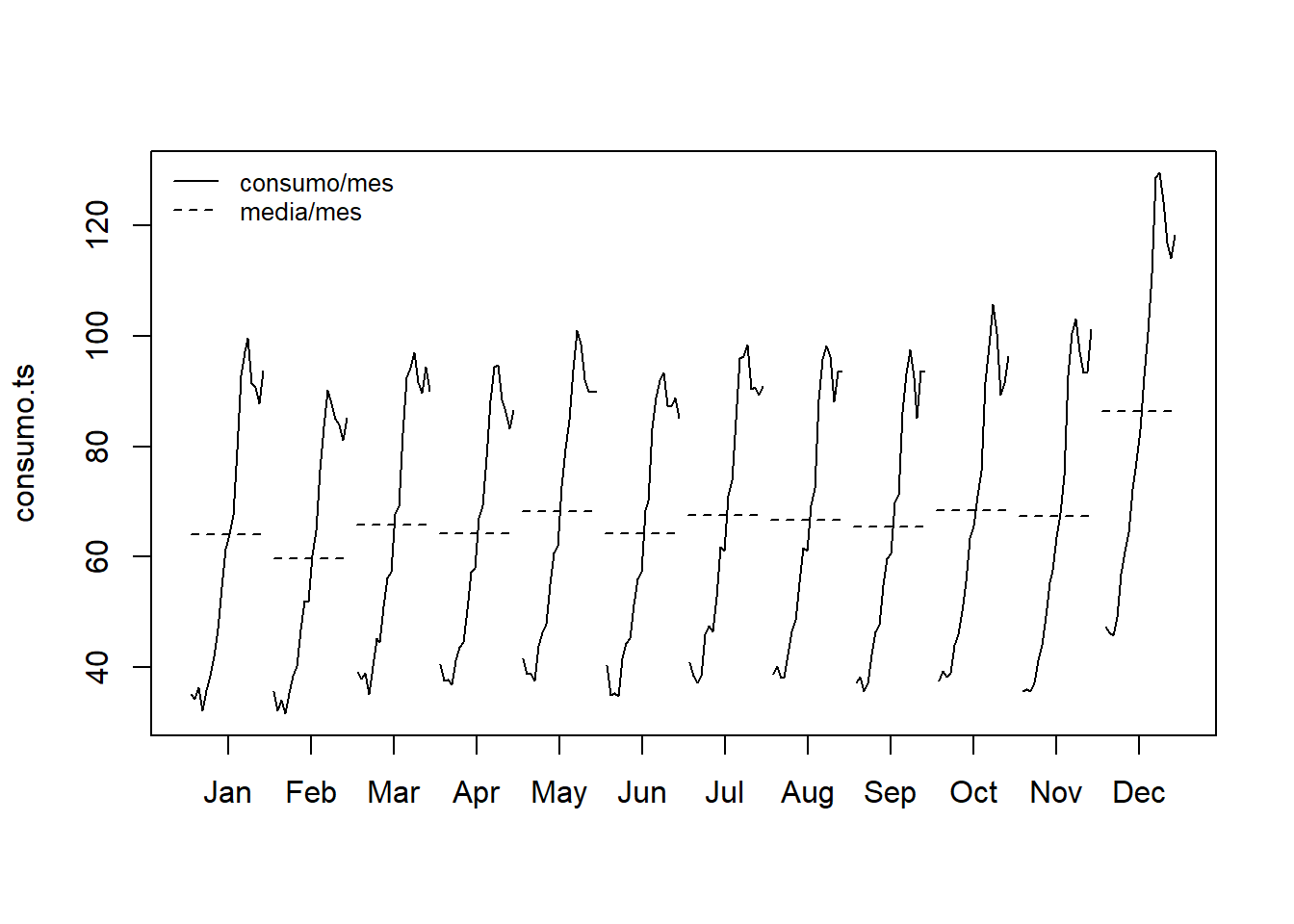
options(digits = 6)Rodando o X13 ARIMA-SEATS automático
library(seasonal)
ajuste <- seas(x = consumo.ts)Neste caso, o programa faz as seguintes avaliações no automático: 1. Verificar teste de sazonalidade QS; A hipótese nula do teste QS é de não haver sazonalidade; - se P-value=0 => tem sazonalidade; 2. Diagnosticar pre-ajuste e modelo ARIMA; 3. Verificar indicios de sazonalidade ou efeitos de dias uteis graficamente; 4. Estabilidade do ajuste sazonal.
# specserie<-spec.ar(consumo.ts) specserie
qs(ajuste) # faz o teste QS para sazonalidade qs p-val
qsori 401.53016 0.00000
qsorievadj 413.70084 0.00000
qsrsd 0.01129 0.99437
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.00000 1.00000
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 157.51593 0.00000
qssrsd 0.02656 0.98681
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste) # mostra os resultados da estimacao ARIMA automatica e outliers detectados
Call:
seas(x = consumo.ts)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Mon -0.00750 0.00299 -2.51 0.0121 *
Tue 0.00415 0.00302 1.38 0.1689
Wed -0.00304 0.00302 -1.01 0.3136
Thu 0.00656 0.00301 2.18 0.0293 *
Fri 0.00564 0.00297 1.90 0.0576 .
Sat 0.00273 0.00301 0.91 0.3645
Easter[15] 0.02240 0.00603 3.71 0.0002 ***
AO2011.May 0.09444 0.02037 4.63 3.6e-06 ***
MA-Nonseasonal-01 0.25901 0.06416 4.04 5.4e-05 ***
MA-Seasonal-12 0.62511 0.05423 11.53 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 920, BIC: 956 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 30.4 Shapiro (normality): 0.995 final(ajuste) # mostra a serie ajustada Jan Feb Mar Apr May Jun Jul Aug
2000 39.3300 39.5505 39.4395 40.1428 40.3741 41.2593 40.0219 38.0183
2001 37.9094 37.1737 37.9657 37.7401 37.3143 36.1452 37.7736 39.3231
2002 39.7687 39.1410 38.7496 38.4960 37.4410 37.0553 36.5095 37.0814
2003 35.2496 36.4043 36.3683 36.7113 35.8835 36.8316 37.1479 37.7011
2004 38.9672 39.6054 41.1016 41.3233 43.1107 43.1698 44.0771 42.4076
2005 42.8621 44.2698 45.2394 44.7964 45.3881 45.9583 46.5637 46.4023
2006 46.1595 46.0124 45.7515 45.6118 46.8711 46.7904 46.6203 47.8558
2007 50.6874 53.3260 51.5483 53.0344 53.3142 53.3089 53.1680 54.5771
Sep Oct Nov Dec
2000 37.8608 37.6293 37.7240 37.9952
2001 39.1803 38.9487 37.6451 37.4916
2002 36.8762 37.3688 37.1320 36.7815
2003 37.8514 38.0284 39.2811 39.0132
2004 42.8546 43.3296 43.2495 44.3708
2005 46.6471 45.8362 45.7397 47.0622
2006 48.1642 49.9190 50.7424 50.4282
2007 56.1715 55.0249 56.2822 57.2221
[ reached getOption("max.print") -- omitted 12 rows ]plot(ajuste) # grafico da serie ajustada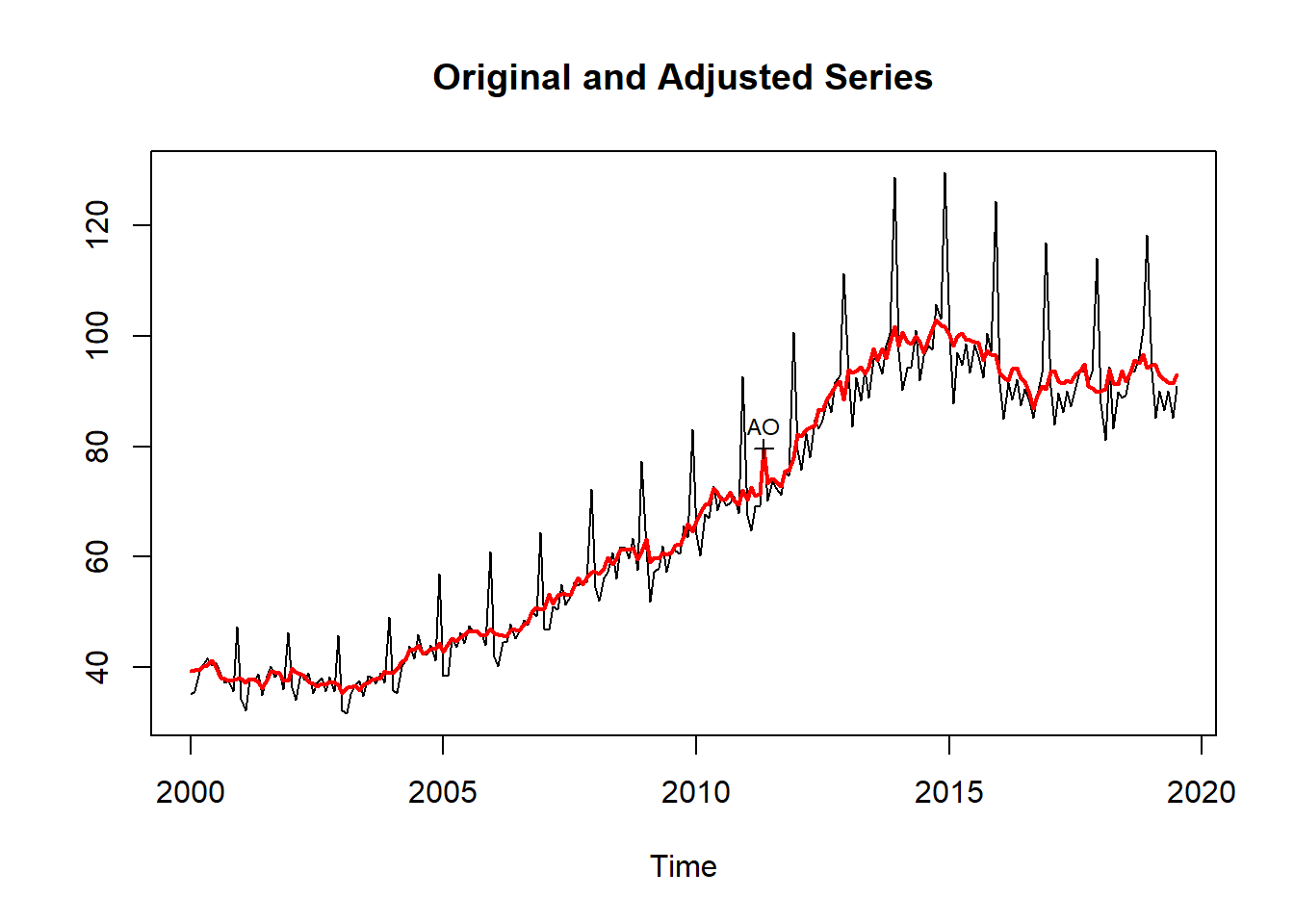
Ajuste manual da série ajustada
Pode-se utilizar a especificação do static para ajustar manualmente a especificação do spec do X13 ARIMA-SEATS.O static mostra o que foi feito e facilita a alteração de algum item específico.
static(ajuste) # permite o ajuste manual do seasseas(x = consumo.ts, regression.variables = c("td", "easter[15]",
"ao2011.May"), arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")O static permite o ajuste manual do seas. Farei um cenário incluindo uma level shift em maio de 2016.
# cenario ajustemanual
ajustemanual <- seas(x = consumo.ts, regression.variables = c("td", "easter[15]",
"ao2011.May", "ls2016.May"), arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")
summary(ajustemanual)
Call:
seas(x = consumo.ts, transform.function = "log", regression.aictest = NULL,
outlier = NULL, regression.variables = c("td", "easter[15]",
"ao2011.May", "ls2016.May"), arima.model = "(0 1 1)(0 1 1)")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Mon -0.007495 0.002989 -2.51 0.01216 *
Tue 0.004147 0.003015 1.38 0.16900
Wed -0.003043 0.003020 -1.01 0.31359
Thu 0.006561 0.003016 2.18 0.02958 *
Fri 0.005632 0.002970 1.90 0.05796 .
Sat 0.002721 0.003024 0.90 0.36812
Easter[15] 0.022408 0.006049 3.70 0.00021 ***
AO2011.May 0.094415 0.020391 4.63 3.7e-06 ***
LS2016.May -0.000648 0.024800 -0.03 0.97915
MA-Nonseasonal-01 0.259104 0.064163 4.04 5.4e-05 ***
MA-Seasonal-12 0.625159 0.054230 11.53 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 922, BIC: 962 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 30.5 Shapiro (normality): 0.995 # comparando com o ajuste automático, vejo que não ajudou com ls2016
summary(ajuste)
Call:
seas(x = consumo.ts)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Mon -0.00750 0.00299 -2.51 0.0121 *
Tue 0.00415 0.00302 1.38 0.1689
Wed -0.00304 0.00302 -1.01 0.3136
Thu 0.00656 0.00301 2.18 0.0293 *
Fri 0.00564 0.00297 1.90 0.0576 .
Sat 0.00273 0.00301 0.91 0.3645
Easter[15] 0.02240 0.00603 3.71 0.0002 ***
AO2011.May 0.09444 0.02037 4.63 3.6e-06 ***
MA-Nonseasonal-01 0.25901 0.06416 4.04 5.4e-05 ***
MA-Seasonal-12 0.62511 0.05423 11.53 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 920, BIC: 956 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 30.4 Shapiro (normality): 0.995 Comentário: embora tenha saído um ajuste, o programa não consegue visualizar adequadamente a time series, colocando ajustes de dias da semana de forma inadequada, uma vez que a série é mensal.
Forecasts do ajuste
ajuste.fcst <- series(ajuste, c("forecast.forecasts"))
autoplot(ajuste.fcst)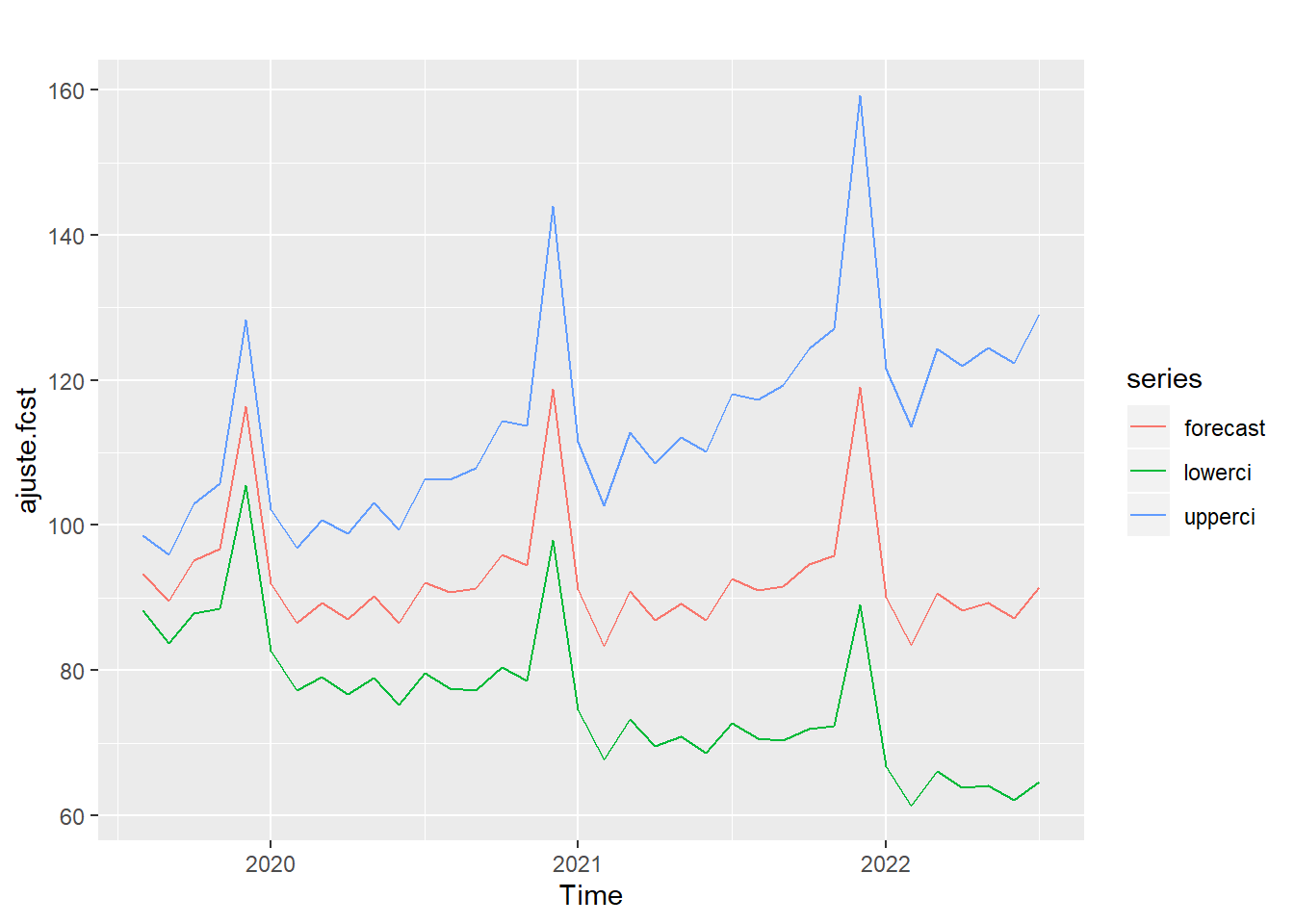
Correção do ajuste automático
Construção dos dias Úteis (building working days)
Vou carregar a partir do sítio eletrônico do Prof. Pedro Costa Ferreira.
library(RCurl)
usingR_url_wd <- getURL("https://raw.githubusercontent.com/pedrocostaferreira/Articles/master/using-R-to-teach-seasonal-adjustment/work_days.csv")
wd <- read.csv2(text = usingR_url_wd)
head(wd)FALSE date Workdays days not_Workdays Workdays_ok.
FALSE 1 jan/70 21 31 10 -4.0
FALSE 2 fev/70 19 28 9 -3.5
FALSE 3 mar/70 21 31 10 -4.0
FALSE 4 abr/70 21 30 9 -1.5
FALSE 5 mai/70 19 31 12 -11.0
FALSE 6 jun/70 22 30 8 2.0# outra opcao é pegar direto do arquivo csv, dentro desta pasta uteis <-
# ts(du[,5], start = c(1970,1), freq = 12)
Workdays_ok <- ts(wd[, 5], start = c(1970, 1), freq = 12)
# building moving holidays (mh) feriados moveis construção dos feriados móveis -
# Pascoa, Carnaval, Natal e Ano Novo feriados <- read.csv2('feriados_moveis.csv')
# head(feriados)
usingR_url_mh <- getURL("https://raw.githubusercontent.com/pedrocostaferreira/Articles/master/using-R-to-teach-seasonal-adjustment/moving_holidays.csv")
mh <- read.csv2("feriados.csv")
# mh <- read.csv2(text = usingR_url_mh) outra opcao é pegar direto do arquivo
# csv, dentro desta pasta
head(mh) # Pascoa e Carnaval, Natal e Ano NovoFALSE Year Easter Carnival Natal NewYear
FALSE 1 1951 25/03/1951 06/02/1951 25/12/1951 01/01/1951
FALSE 2 1952 13/04/1952 26/02/1952 25/12/1952 01/01/1952
FALSE 3 1953 05/04/1953 17/02/1953 25/12/1953 01/01/1953
FALSE 4 1954 18/04/1954 02/03/1954 25/12/1954 01/01/1954
FALSE 5 1955 10/04/1955 22/02/1955 25/12/1955 01/01/1955
FALSE 6 1956 01/04/1956 14/02/1956 25/12/1956 01/01/1956# Easter Pascoa
dates.easter <- as.Date(as.character(mh$Easter), "%d/%m/%Y")
easter <- genhol(dates.easter, start = -8, end = 1, frequency = 12)
# Carnival
dates.carnival <- as.Date(as.character(mh$Carnival), "%d/%m/%Y")
carnival <- genhol(dates.carnival, start = -3, end = 1, frequency = 12, center = "calendar")
# Ampliação para Natal e Ano Novo
# Natal
dates.natal <- as.Date(as.character(mh$Natal), "%d/%m/%Y")
natal <- genhol(dates.natal, start = -10, end = 5, frequency = 12, center = "calendar")
# NewYear
dates.anonovo <- as.Date(as.character(mh$NewYear), "%d/%m/%Y")
anonovo <- genhol(dates.anonovo, start = -10, end = 5, frequency = 12, center = "calendar")
regs <- na.omit(cbind(Workdays_ok, easter, carnival))
regs2 <- na.omit(cbind(Workdays_ok, easter))
head(regs)FALSE Workdays_ok easter carnival
FALSE Jan 1970 -4.0 0 0.000000
FALSE Feb 1970 -3.5 0 0.203125
FALSE Mar 1970 -4.0 1 -0.203125
FALSE Apr 1970 -1.5 0 0.000000
FALSE May 1970 -11.0 0 0.000000
FALSE Jun 1970 2.0 0 0.000000regsamp <- na.omit(cbind(Workdays_ok, easter, carnival, anonovo))
# obs: embora tenha criado esta rotina, o programa identificou problemas de
# multicolinearidade e conflito do anonovo com adittive outlier
head(regsamp)FALSE Workdays_ok easter carnival anonovo
FALSE Jan 1970 -4.0 0 0.000000 0.00290698
FALSE Feb 1970 -3.5 0 0.203125 0.00000000
FALSE Mar 1970 -4.0 1 -0.203125 0.00000000
FALSE Apr 1970 -1.5 0 0.000000 0.00000000
FALSE May 1970 -11.0 0 0.000000 0.00000000
FALSE Jun 1970 2.0 0 0.000000 0.00000000Agora faz-se novamente a estimação com os dados de dias úteis e feriados brasileiros. Primeiro, farei sem especificar os outliers.
ajuste2 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL, regression.usertype = "holiday",
forecast.save = "forecasts")
qs(ajuste2) qs p-val
qsori 401.53016 0.00000
qsorievadj 402.57808 0.00000
qsrsd 0.88286 0.64312
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.00000 1.00000
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 152.25008 0.00000
qssrsd 1.30197 0.52153
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste2)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
xreg1 0.001390 0.000492 2.82 0.0047 **
xreg2 0.018693 0.008190 2.28 0.0225 *
xreg3 -0.013760 0.008106 -1.70 0.0896 .
MA-Nonseasonal-01 0.395768 0.060655 6.52 6.8e-11 ***
MA-Seasonal-12 0.627773 0.054518 11.51 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 968, BIC: 988 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 33.9 . Shapiro (normality): 0.996 Agora com os outliers predefinidos. Verá que melhorou um pouco, reduzindo o AICc.
ajuste3 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL, regression.variables = c("ls2016.May",
"AO2011.May", "AO2009.Jan"), regression.usertype = "holiday", forecast.save = "forecasts")
qs(ajuste3) qs p-val
qsori 401.53016 0.00000
qsorievadj 407.23799 0.00000
qsrsd 0.72962 0.69433
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.00000 1.00000
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 152.53446 0.00000
qssrsd 0.95047 0.62174
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste3)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
regression.variables = c("ls2016.May", "AO2011.May", "AO2009.Jan"),
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO2009.Jan 0.09040 0.02243 4.03 5.6e-05 ***
AO2011.May 0.06688 0.02248 2.97 0.0029 **
LS2016.May -0.02424 0.02552 -0.95 0.3421
xreg1 0.00137 0.00046 2.99 0.0028 **
xreg2 0.01951 0.00765 2.55 0.0107 *
xreg3 -0.01294 0.00755 -1.71 0.0865 .
MA-Nonseasonal-01 0.36381 0.06152 5.91 3.3e-09 ***
MA-Seasonal-12 0.62358 0.05502 11.33 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 950, BIC: 980 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 31.2 Shapiro (normality): 0.997 Fazendo a acurácia do modelo.
library(Metrics)
# mae(actual, predicted) rmse(actual, predicted)
predicted <- final(ajuste3)
actual <- consumo.ts
forecast::accuracy(predicted, actual) ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set -0.206603 6.36652 3.64985 -1.01552 5.21183 -0.00996298 0.72423# idem ao obtido no Metrics abaixo
(mae3 <- mae(actual, predicted))[1] 3.64985(rmse3 <- rmse(actual, predicted))[1] 6.36652Verifico a especificação do ajuste3.
static(ajuste3) # permite o ajuste manual do seasseas(x = consumo.ts, xreg = regs, regression.variables = c("ao2009.Jan",
"ao2011.May", "ls2016.May"), regression.usertype = "holiday",
forecast.save = "forecasts", arima.model = "(0 1 1)(0 1 1)",
regression.aictest = NULL, outlier = NULL, transform.function = "log")Vou avaliar a retirada de ls2016 não significativo em ajuste3.
require(seasonal)
#
ajuste4 <- seas(x = consumo.ts, xreg = regs, regression.variables = c("AO2011.May",
"AO2009.Jan"), regression.usertype = "holiday", forecast.save = "forecasts",
regression.aictest = NULL, outlier = NULL)
qs(ajuste4) qs p-val
qsori 401.53016 0.00000
qsorievadj 407.88433 0.00000
qsrsd 0.80386 0.66903
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.00000 1.00000
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 152.32568 0.00000
qssrsd 1.08601 0.58100
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste4)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
outlier = NULL, regression.variables = c("AO2011.May", "AO2009.Jan"),
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO2009.Jan 0.090419 0.022427 4.03 5.5e-05 ***
AO2011.May 0.067174 0.022479 2.99 0.0028 **
xreg1 0.001358 0.000459 2.96 0.0031 **
xreg2 0.018826 0.007608 2.47 0.0133 *
xreg3 -0.013312 0.007533 -1.77 0.0772 .
MA-Nonseasonal-01 0.359732 0.061636 5.84 5.3e-09 ***
MA-Seasonal-12 0.621562 0.055065 11.29 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 949, BIC: 975 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 31.7 Shapiro (normality): 0.997 predicted4 <- final(ajuste4)
actual <- consumo.ts
forecast::accuracy(predicted4, actual) ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set -0.207287 6.3667 3.65141 -1.01648 5.21273 -0.00849573 0.724218# idem ao obtido no Metrics abaixo
require(Metrics)
(mae4 <- mae(actual, predicted4))[1] 3.65141(rmse4 <- rmse(actual, predicted4))[1] 6.3667static(ajuste4)seas(x = consumo.ts, xreg = regs, regression.variables = c("ao2009.Jan",
"ao2011.May"), regression.usertype = "holiday", forecast.save = "forecasts",
arima.model = "(0 1 1)(0 1 1)", regression.aictest = NULL,
outlier = NULL, transform.function = "log")Melhorou pelo AICc e significancia e acurácia. Vou checar mais uma alternativa alterando o ARIMA conforme o obtido em https://rpubs.com/amrofi/arima_varejoms, ARIMA(4,1,0)(0,1,1)[12].
# com especificação do ARIMA
ajuste5 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL, regression.variables = c("AO2011.May",
"AO2009.Jan"), arima.model = "(3 1 0)(0 1 1)", regression.usertype = "holiday",
forecast.save = "forecasts")
qs(ajuste5) qs p-val
qsori 401.53016 0.00000
qsorievadj 407.96642 0.00000
qsrsd 0.72012 0.69763
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.02259 0.98877
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 152.39745 0.00000
qssrsd 0.95080 0.62164
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste5)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
regression.variables = c("AO2011.May", "AO2009.Jan"), arima.model = "(3 1 0)(0 1 1)",
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO2009.Jan 0.088661 0.021967 4.04 5.4e-05 ***
AO2011.May 0.068433 0.021982 3.11 0.0019 **
xreg1 0.001316 0.000494 2.66 0.0078 **
xreg2 0.021200 0.007611 2.79 0.0053 **
xreg3 -0.011816 0.007530 -1.57 0.1166
AR-Nonseasonal-01 -0.381062 0.066003 -5.77 7.8e-09 ***
AR-Nonseasonal-02 -0.089895 0.070551 -1.27 0.2026
AR-Nonseasonal-03 0.093884 0.065988 1.42 0.1548
MA-Seasonal-12 0.621361 0.054694 11.36 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (3 1 0)(0 1 1) Obs.: 235 Transform: log
AICc: 949, BIC: 982 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 28.7 Shapiro (normality): 0.997 Comentário: o melhor modelo foi o ajuste4.
Testei com level shift para maio de 2017 e não ajudou.
require(seasonal)
#
ajuste6 <- seas(x = consumo.ts, xreg = regs, regression.variables = c("AO2011.May",
"AO2009.Jan", "ls2017.May"), regression.usertype = "holiday", forecast.save = "forecasts",
regression.aictest = NULL, outlier = NULL)
qs(ajuste6) qs p-val
qsori 401.53016 0.00000
qsorievadj 407.42904 0.00000
qsrsd 0.81383 0.66570
qssadj 0.00000 1.00000
qssadjevadj 0.00000 1.00000
qsirr 0.00000 1.00000
qsirrevadj 0.00000 1.00000
qssori 152.62432 0.00000
qssorievadj 152.17610 0.00000
qssrsd 1.08365 0.58168
qsssadj 0.00000 1.00000
qsssadjevadj 0.00000 1.00000
qssirr 0.00000 1.00000
qssirrevadj 0.00000 1.00000summary(ajuste6)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
outlier = NULL, regression.variables = c("AO2011.May", "AO2009.Jan",
"ls2017.May"), regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO2009.Jan 0.090486 0.022418 4.04 5.4e-05 ***
AO2011.May 0.067037 0.022474 2.98 0.0029 **
LS2017.May -0.008531 0.025883 -0.33 0.7417
xreg1 0.001371 0.000461 2.97 0.0029 **
xreg2 0.018752 0.007607 2.46 0.0137 *
xreg3 -0.013282 0.007529 -1.76 0.0777 .
MA-Nonseasonal-01 0.358471 0.061663 5.81 6.1e-09 ***
MA-Seasonal-12 0.622614 0.055040 11.31 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 951, BIC: 981 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 31.3 Shapiro (normality): 0.997 predicted6 <- final(ajuste6)
actual <- consumo.ts
forecast::accuracy(predicted6, actual) ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set -0.209946 6.36654 3.65157 -1.02048 5.21332 -0.00905445 0.724206# idem ao obtido no Metrics abaixo
require(Metrics)
(mae6 <- mae(actual, predicted6))[1] 3.65157(rmse6 <- rmse(actual, predicted6))[1] 6.36654static(ajuste6)seas(x = consumo.ts, xreg = regs, regression.variables = c("ao2009.Jan",
"ao2011.May", "ls2017.May"), regression.usertype = "holiday",
forecast.save = "forecasts", arima.model = "(0 1 1)(0 1 1)",
regression.aictest = NULL, outlier = NULL, transform.function = "log")Fiz uso do seasonalview::view para obter um refinamento do modelo, a partir do ajuste5. É possível verificar que o modelo melhora com a especificação do ajuste7.
library(seasonalview)
# view(ajuste5) script do shiny
ajuste7 <- seas(x = consumo.ts, xreg = regs, regression.aictest = NULL, regression.variables = c("AO2011.May",
"AO2009.Jan"), arima.model = "(2 1 1)(0 1 1)", regression.usertype = "holiday",
forecast.save = "forecasts")
summary(ajuste7)
Call:
seas(x = consumo.ts, xreg = regs, regression.aictest = NULL,
regression.variables = c("AO2011.May", "AO2009.Jan"), arima.model = "(2 1 1)(0 1 1)",
regression.usertype = "holiday", forecast.save = "forecasts")
Coefficients:
Estimate Std. Error z value Pr(>|z|)
AO2009.Jan 0.088026 0.021870 4.02 5.7e-05 ***
AO2011.May 0.065013 0.021902 2.97 0.0030 **
xreg1 0.001299 0.000493 2.64 0.0084 **
xreg2 0.020741 0.007548 2.75 0.0060 **
xreg3 -0.012047 0.007450 -1.62 0.1059
AR-Nonseasonal-01 -0.987530 0.206865 -4.77 1.8e-06 ***
AR-Nonseasonal-02 -0.346695 0.077358 -4.48 7.4e-06 ***
MA-Nonseasonal-01 -0.609473 0.212446 -2.87 0.0041 **
MA-Seasonal-12 0.617472 0.054676 11.29 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
SEATS adj. ARIMA: (2 1 1)(0 1 1) Obs.: 235 Transform: log
AICc: 948, BIC: 981 QS (no seasonality in final): 0
Box-Ljung (no autocorr.): 23.6 Shapiro (normality): 0.996 Figura dos fatores sazonais
monthplot(ajuste7, col.base = 1)
legend("topleft", legend = c("Irregular", "Seasonal", "Seasonal Average"), col = c(4,
2, 1), lwd = c(1, 2, 2), lty = 1, bty = "n", cex = 0.6)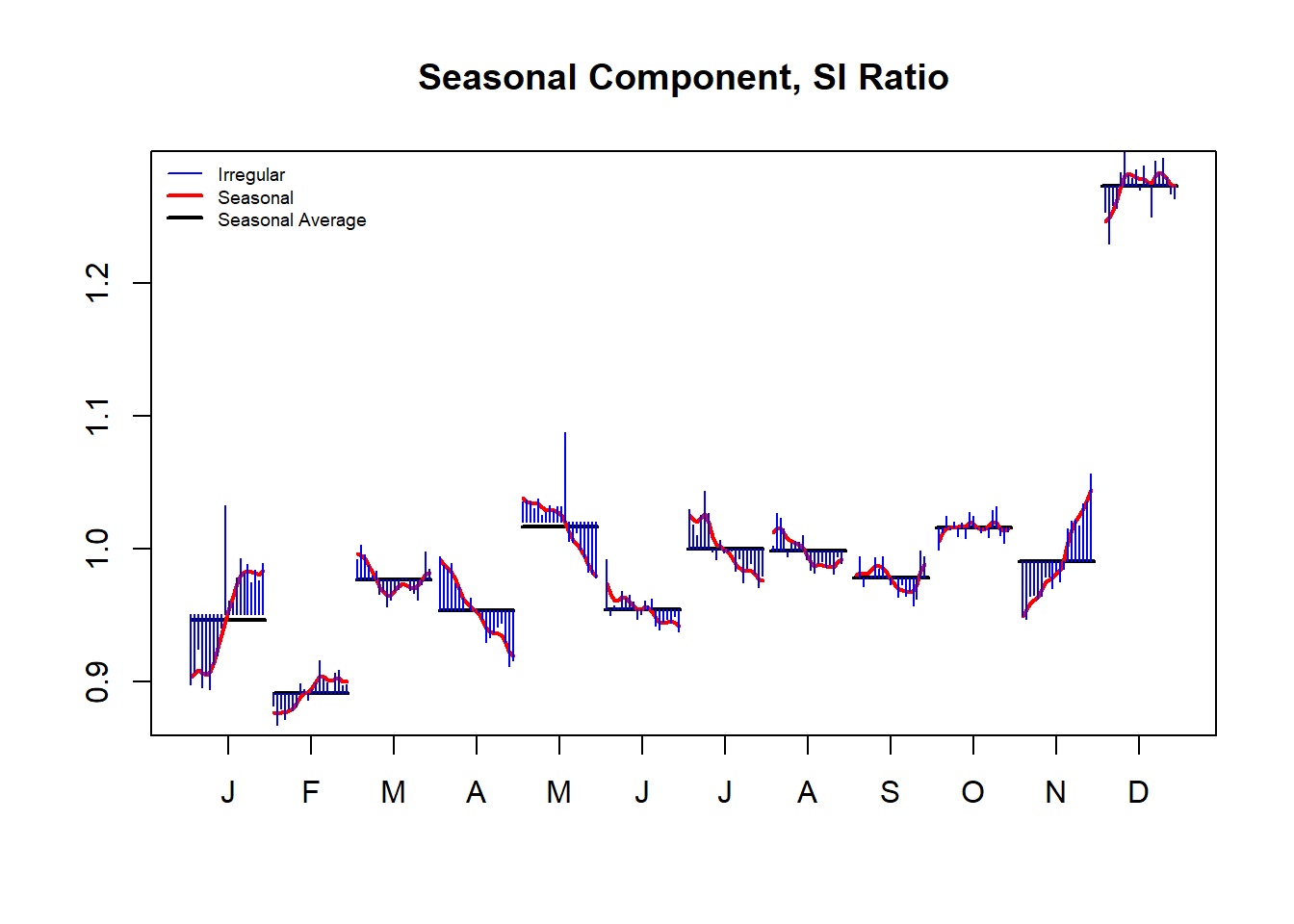
# figura da serie ajustada
plot(ajuste7, main = "Ajuste 7 de consumo.ts")
grid()
legend("topleft", legend = c("Original", "Adjusted"), col = c(1, 2), lwd = c(1, 2),
lty = 1, bty = "n", cex = 0.6)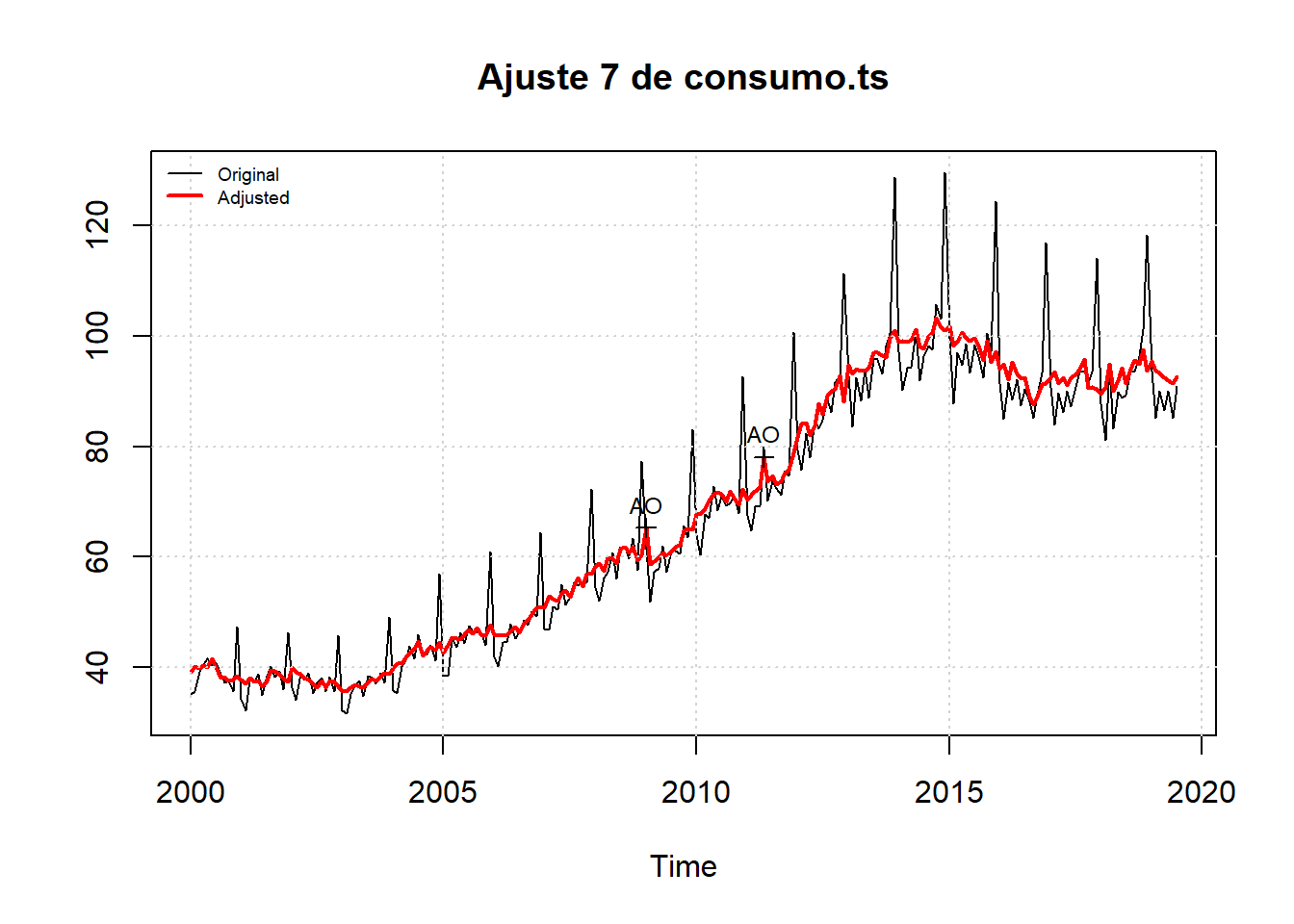
Forecasts do ajuste7
forecasts7 <- series(ajuste7, c("forecast.forecasts"))
require(graphics)
require(zoo)
data.fcst <- cbind.zoo(consumo.ts, series(ajuste7, "forecast.forecasts"))
ts.plot(data.fcst, col = c(1, 2, 3, 4), main = "serie original de consumo e forecasts ajuste7",
xlab = "Mes/Ano")
legend("topleft", lty = 1, pch = 1, col = 1:4, c("data", "X13as", "Lim Inferior",
"Lim Superior"))
grid()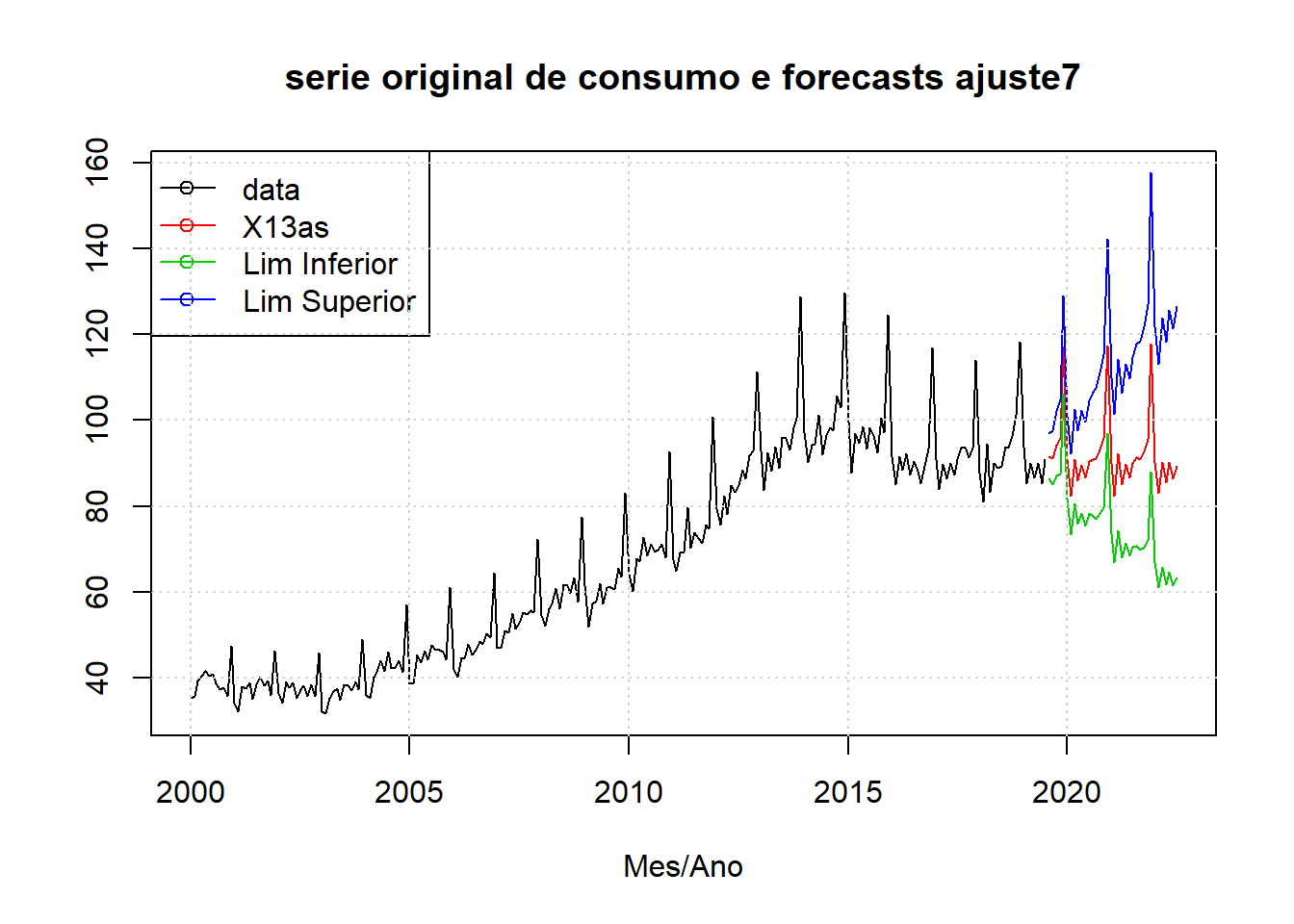
list(forecasts7)[[1]]
forecast lowerci upperci
Aug 2019 91.5024 86.3002 97.0182
Sep 2019 91.0369 84.9747 97.5315
Oct 2019 94.3149 87.1782 102.0358
Nov 2019 95.8695 87.6102 104.9075
Dec 2019 117.0635 106.1817 129.0605
Jan 2020 90.8174 81.6707 100.9885
Feb 2020 82.2767 73.4446 92.1710
Mar 2020 90.8880 80.5582 102.5424
Apr 2020 86.0581 75.7910 97.7160
May 2020 89.5263 78.3563 102.2887
Jun 2020 86.6995 75.4371 99.6432
Jul 2020 90.4649 78.2656 104.5658
Aug 2020 90.9903 77.6948 106.5609
Sep 2020 91.0194 77.0286 107.5514
Oct 2020 93.2418 78.2199 111.1486
Nov 2020 95.8195 79.6586 115.2591
Dec 2020 117.4116 96.8378 142.3564
Jan 2021 89.8902 73.5364 109.8809
Feb 2021 82.4448 66.9419 101.5382
Mar 2021 92.1331 74.2568 114.3130
Apr 2021 85.0685 68.0859 106.2872
May 2021 89.8199 71.3990 112.9934
Jun 2021 86.5924 68.3761 109.6617
Jul 2021 89.9424 70.5623 114.6453
Aug 2021 91.2909 70.7465 117.8012
Sep 2021 90.9064 69.7949 118.4036
Oct 2021 92.7030 70.5194 121.8651
Nov 2021 95.7003 72.1191 126.9921
Dec 2021 117.7998 88.0123 157.6688
Jan 2022 90.1874 66.8013 121.7606
Feb 2022 83.1171 61.0589 113.1440
Mar 2022 90.2201 65.7405 123.8151
Apr 2022 85.4589 61.7776 118.2178
[ reached getOption("max.print") -- omitted 3 rows ]require(xlsx)
write.xlsx(as.data.frame.ts(forecasts7), "forecasts.xlsx", col.names = TRUE, row.names = TRUE)Opção gráfica
library(dygraphs)
dygraph(data.fcst, main = "Índice de consumo do varejo de Mato Grosso do Sul") %>%
dyAxis("y", label = "Índice", valueRange = c(0, 150), axisLabelFontSize = 20) %>%
dyAxis("x", label = "Mês/Ano", axisLabelFontSize = 20) %>% dyGroup(c("consumo.ts",
"forecast"), drawPoints = TRUE, color = c("blue", "red")) %>% dyLegend(width = 400) %>%
dyAnnotation("2009-1-1", text = "AOjan09", attachAtBottom = TRUE, width = 80) %>%
dyAnnotation("2011-5-1", text = "AOmai11", attachAtBottom = TRUE, width = 80) %>%
dyAnnotation("2016-5-1", text = "LSmai16", attachAtBottom = TRUE, width = 80) %>%
dyOptions(drawPoints = TRUE, pointSize = 5, pointShape = "triangle", axisLineWidth = 1.5)Agora que já temos as informações até fev/2020, podemos comparar as estimativas com os dados reais.
# dadosnovos<-BETS::BETSget(1479)
dadosnovos <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6,
35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3,
36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6,
35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3,
43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3,
47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5,
47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6,
55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7,
77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1,
64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5,
64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7,
82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5,
88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4,
101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6,
93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4,
90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5,
93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5,
96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 91, 94.4, 93.4, 95.9, 102.6,
116, 94.9, 89.1), .Tsp = c(2000, 2020.08333333333, 12), class = "ts")
# View(cbind.zoo(data.fcst,dadosnovos))
print(cbind.zoo(data.fcst, dadosnovos)[230:242]) consumo.ts forecast lowerci upperci dadosnovos
fev 2019 85.2 NA NA NA 85.2
mar 2019 90.0 NA NA NA 90.0
abr 2019 86.6 NA NA NA 86.6
mai 2019 90.0 NA NA NA 90.0
jun 2019 85.2 NA NA NA 85.2
jul 2019 90.9 NA NA NA 91.0
ago 2019 NA 91.5024 86.3002 97.0182 94.4
set 2019 NA 91.0369 84.9747 97.5315 93.4
out 2019 NA 94.3149 87.1782 102.0358 95.9
nov 2019 NA 95.8695 87.6102 104.9075 102.6
dez 2019 NA 117.0635 106.1817 129.0605 116.0
jan 2020 NA 90.8174 81.6707 100.9885 94.9
fev 2020 NA 82.2767 73.4446 92.1710 89.1Acurácia do período Agosto/2019 a fev/2020:
previsto <- forecasts7[1:7, 1]
observado <- dadosnovos[236:242]
forecast::accuracy(previsto, observado) ME RMSE MAE MPE MAPE
Test set 3.34553 4.24513 3.64939 3.55081 3.81275Ou seja, um erro percentual médio de 3.55% e um erro absoluto médio de 3.64%.
Referências
FERREIRA, Pedro Costa; SPERANZA, Talitha; COSTA, Jonatha (2018). BETS: Brazilian Economic Time Series. R package version 0.4.9. Disponível em: https://CRAN.R-project.org/package=BETS.
FERREIRA, Pedro C.; MATOS, Daiane M. Usando o R para ensinar Ajuste Sazonal. São Paulo: FGV, 2017. 18p. Disponível em: http://portalibre.fgv.br/lumis/portal/file/fileDownload.jsp?fileId=8A7C82C5519A547801533DF7BE5E2D0D
HYNDMAN, Rob. (2018). fpp2: Data for “Forecasting: Principles and Practice” (2nd Edition). R package version 2.3. Disponível em: https://CRAN.R-project.org/package=fpp2.
HYNDMAN, R.J., & ATHANASOPOULOS, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. Disponível em: https://otexts.com/fpp2/. Accessed on 12 Set 2019.
SAX, C; EDDELBUETTEL, D. (2018). “Seasonal Adjustment by X-13ARIMA-SEATS in R.” Journal of Statistical Software, 87(11), 1-17. doi: 10.18637/jss.v087.i11 (URL: https://doi.org/10.18637/jss.v087.i11).