Séries Temporais com R: Análise Theta para o Consumo do Varejo em MS com pacotes `forecast::thetaf` e `forecTheta`

Last updated on Apr 22, 2020 12 min read

Licença

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0

Citação

Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Séries Temporais com R: Análise Theta para o Consumo do Varejo em MS com pacote forecast::thetaf e forecTheta. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/varejoms_thetaf e em https://adrianofigueiredo.netlify.app/post/series-temporais-theta-consumo-varejo-ms/.

Introdução

Neste arquivo utilizo a série do Índice de volume de vendas no varejo Total de Mato Grosso do Sul, série mensal a partir de jan/2000 até ago/2019 obtida com o pacote BETS e importada do Banco Central do Brasil. Portanto, são 236 observações mensais.

Dados

Farei de duas formas para o leitor. Uma carrega direto do site do Banco Central do Brasil com o pacote BETS (FERREIRA, SPERANZA e COSTA, 2018) e a outra eu gerei a estrutura idêntica pela função dput() para os leitores que não conseguirem por qualquer motivo o acesso ao site do Banco Central (as vezes vejo isso ocorrer dependendo dos bloqueios da sua rede de internet). Esclareço ao leitor que após baixar a série pelo BETS, fiz o dput e a partir de então, desabilitei o bloco (Chunk) que acessa o BETS apenas para agilizar os cálculos.

library(BETS)
# Pegando as séries a partir do site do Banco Central do Brasil
# Índice de volume de vendas no varejo Total de Mato Grosso do Sul
# mensal a partir de jan/2000 até ago/2019 
# 236 observações mensais
varejoms <- BETSget(1479) 
dput(varejoms)  # opção para ter os dados como na structure abaixo
library(BETS)
varejoms <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6, 
    35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3, 
    36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6, 
    35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3, 
    43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3, 
    47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5, 
    47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6, 
    55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7, 
    77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1, 
    64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5, 
    64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7, 
    82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5, 
    88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4, 
    101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6, 
    93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4, 
    90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5, 
    93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5, 
    96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 91, 94.1), .Tsp = c(2000, 
    2019.58333333333, 12), class = "ts")
print(varejoms)
FALSE        Jan   Feb   Mar   Apr   May   Jun   Jul   Aug   Sep   Oct   Nov   Dec
FALSE 2000  35.2  35.6  39.2  40.5  41.6  40.4  40.8  38.7  37.3  37.6  35.6  47.4
FALSE 2001  34.2  32.2  38.0  37.5  38.8  35.0  38.4  40.2  38.2  39.3  36.0  46.3
FALSE 2002  36.4  34.0  39.0  37.8  38.9  35.3  37.2  38.1  35.6  38.3  35.6  45.7
FALSE 2003  32.2  31.6  35.2  36.8  37.5  34.8  38.4  38.1  37.0  39.0  37.3  49.0
FALSE 2004  35.8  35.3  40.2  41.3  43.9  41.6  45.9  42.3  42.2  44.0  41.3  56.9
FALSE 2005  38.5  38.5  45.3  43.6  46.2  44.3  47.5  46.5  46.4  46.0  44.1  61.0
FALSE 2006  42.0  40.2  44.6  44.5  47.8  45.3  46.5  48.5  47.7  50.2  49.3  64.5
FALSE 2007  47.0  46.8  51.0  50.5  55.0  51.3  52.8  55.3  54.8  55.6  55.3  72.2
FALSE  [ reached getOption("max.print") -- omitted 12 rows ]
class(varejoms)
FALSE [1] "ts"
# [1] 'ts'

A rotina de dados obtidos pelo BETS já retorna a série em formato ts, ou seja, série temporal. Farei então a criação de uma série em diferenças para observar o comportamento da série em nível e em diferenças.

Inicialmente olharei as estatísticas descritivas da série. Em seguida farei um plot básico da série e o plot pelo pacote dygraphs, útil para ver os pontos de picos e momentos específicos.

dvarejo <- diff(varejoms)
# estatisticas basicas
summary(varejoms)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  31.60   44.08   64.65   67.39   90.05  129.60 
# plot basico
plot(varejoms)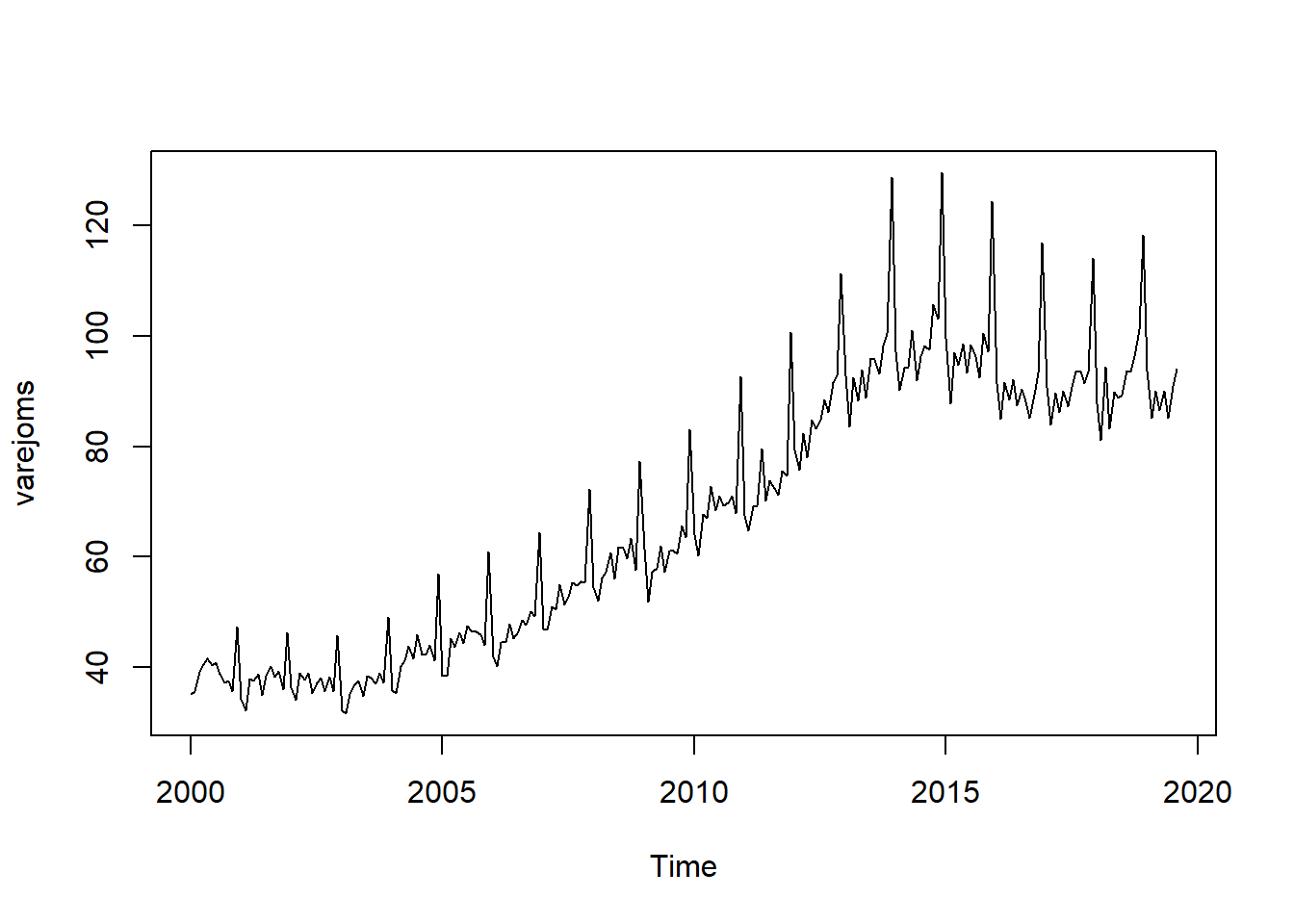

# pelo pacote dygraph dá mais opções
library(dygraphs)
dygraph(varejoms, main = "Índice de volume de vendas no varejo total de Mato Grosso do Sul <br> (Mensal)  (2011=100) BCB 1479") %>% 
    dyAxis("x", drawGrid = TRUE) %>% dyEvent("2005-1-01", "2005", labelLoc = "bottom") %>% 
    dyEvent("2015-1-01", "2015", labelLoc = "bottom") %>% dyEvent("2018-1-01", "2018", 
    labelLoc = "bottom") %>% dyEvent("2019-1-01", "2019", labelLoc = "bottom") %>% 
    dyOptions(drawPoints = TRUE, pointSize = 2)

É possivel visualizar nos plots acima: sazonalidade (por exemplo, picos em dezembro de cada ano); a tendência aparentemente crescente até 2014 e decresce com a “crise” brasileira; e uma aparente não-estacionariedade (média e variância mudam no tempo).

Análise da série

Função de Autocorrelação (FAC) e Autocorrelação parcial (FACp) com defasagem 36

Série em nível

Usarei a rotina do Hyndman e Athanasopoulos (2018).

varejo <- varejoms
varejo %>% forecast::ggtsdisplay(main = "Série de Varejo MS")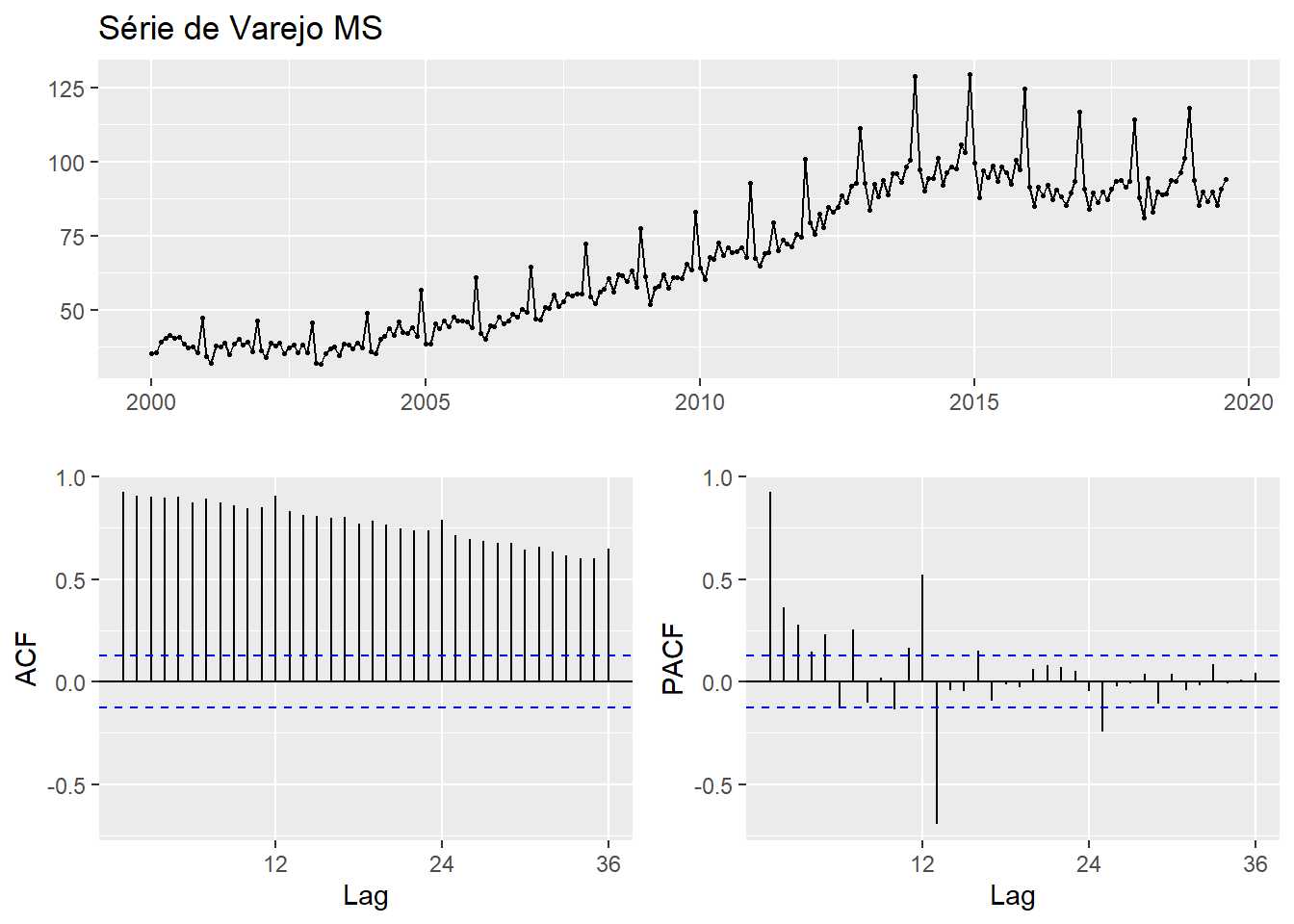

Neste caso, o ggtsdisplay do pacote forecast já retorna os gráficos da série, e respectivas ACF e PACF.

Série em primeira diferença

Como a série apresenta variações sazonais importantes, assim como tendência importante, claramente não-estacionárias, vou olhar também em primeira diferença.

varejo %>% diff() %>% forecast::ggtsdisplay(main = "Série varejo de MS em primeira diferença")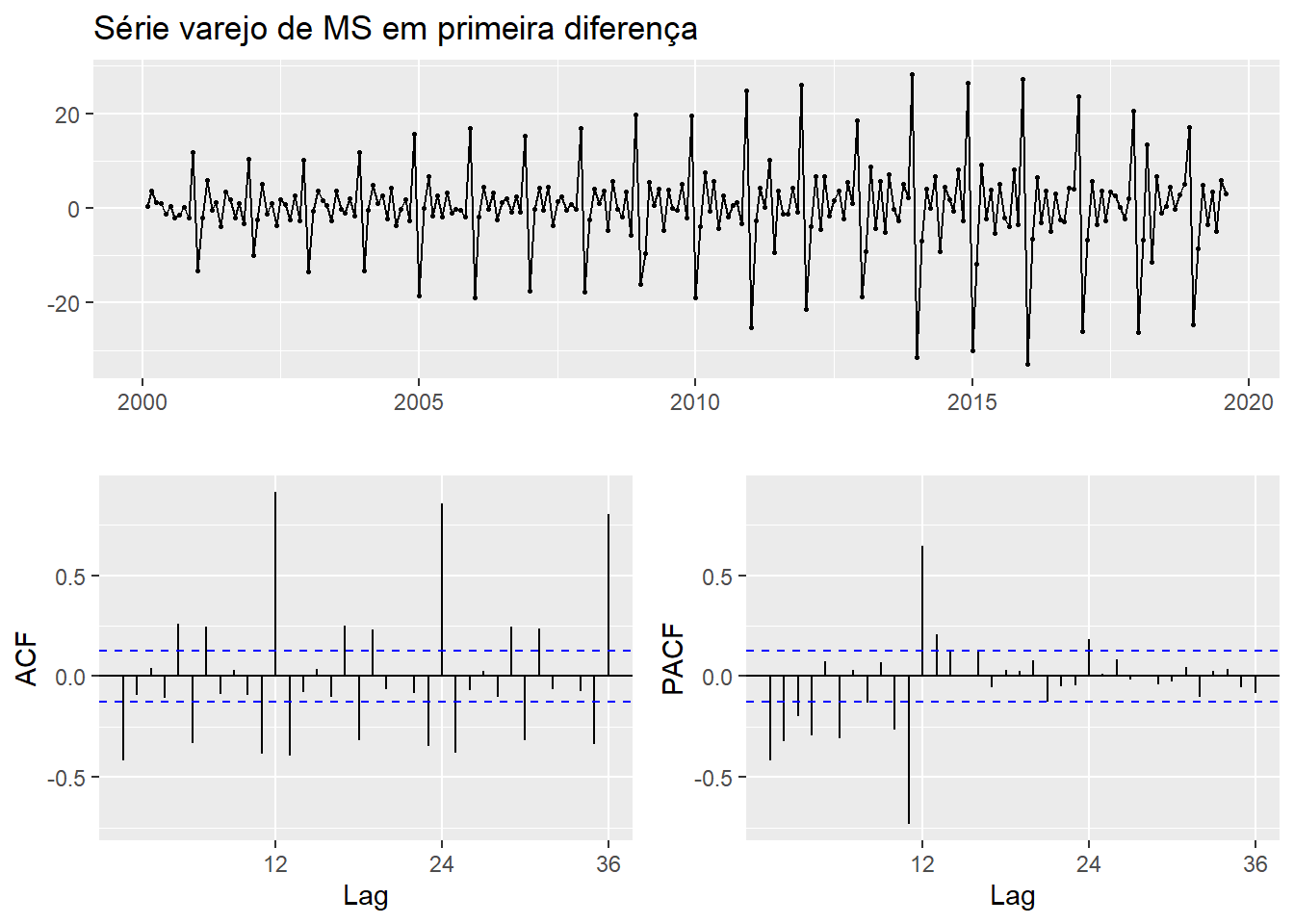

Primeira diferença sazonal e ACF e PACF

Farei agora a diferença sazonal.

varejo %>% diff(lag = 12) %>% forecast::ggtsdisplay(main = "Série varejo de MS em primeira diferença sazonal")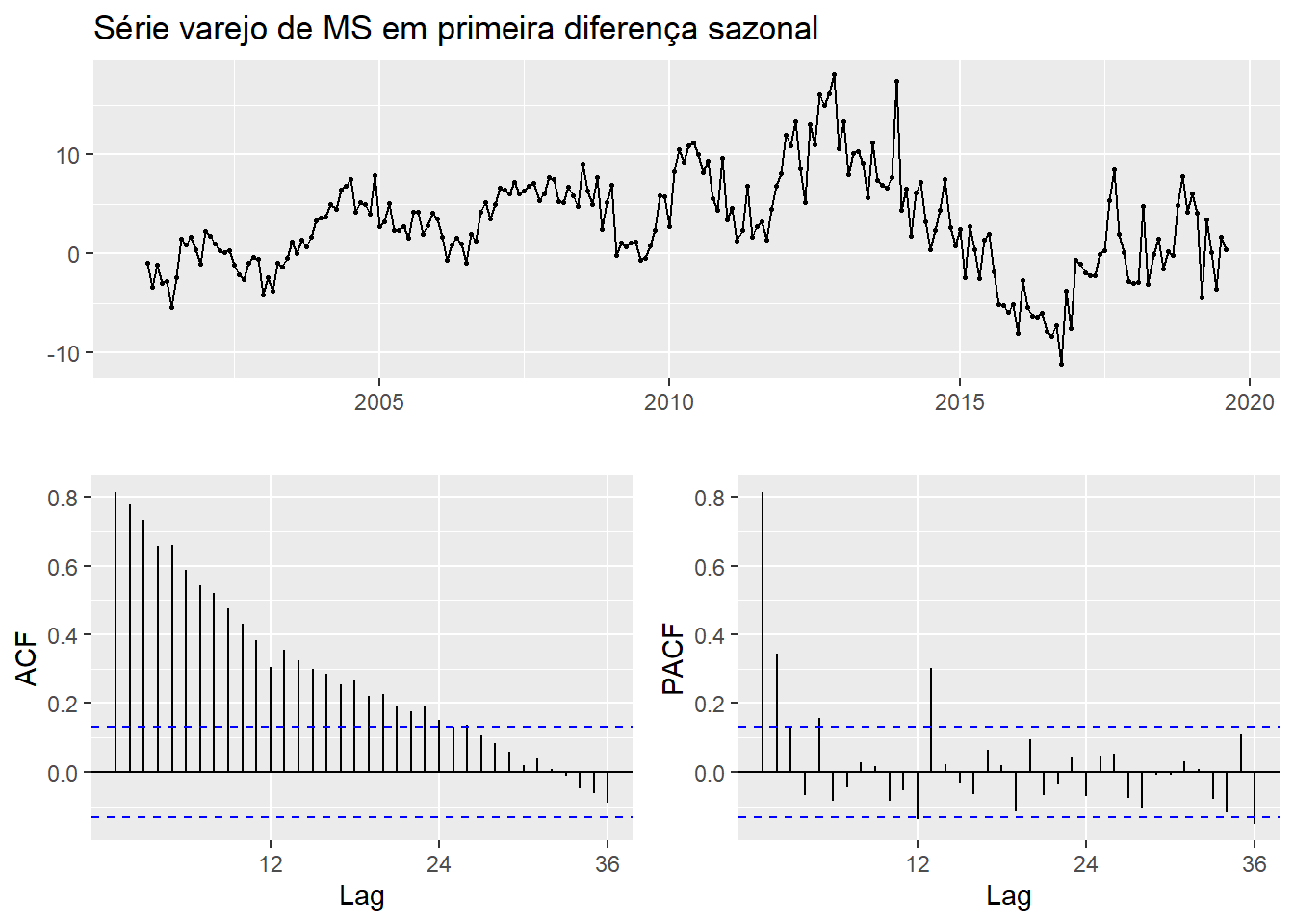

Ajuste sazonal e ACF e PACF

Aplicaremos o ajuste sazonal tipo STL (Seasonal Decomposition of Time Series by Loess) aos dados.

library(fpp2)
varejoadj <- varejo %>% stl(s.window = "periodic") %>% seasadj()
autoplot(varejoadj, main = "Série de Varejo MS com ajuste sazonal STL")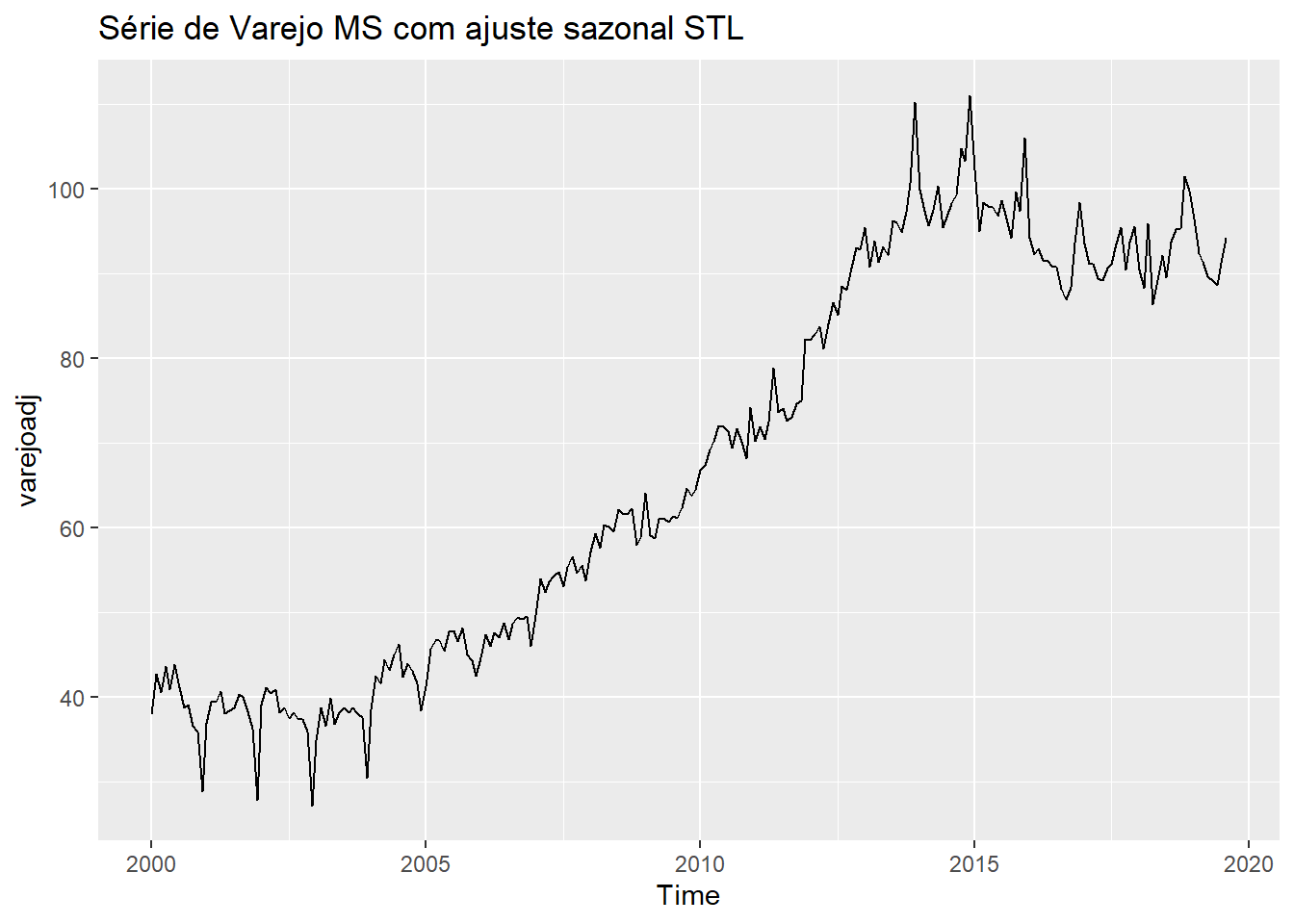

E agora os plots de ACF e PACF na série ajustada sazonalmente.

varejoadj %>% diff() %>% forecast::ggtsdisplay(main = "Série varejo de MS em primeira diferença e ajuste sazonal")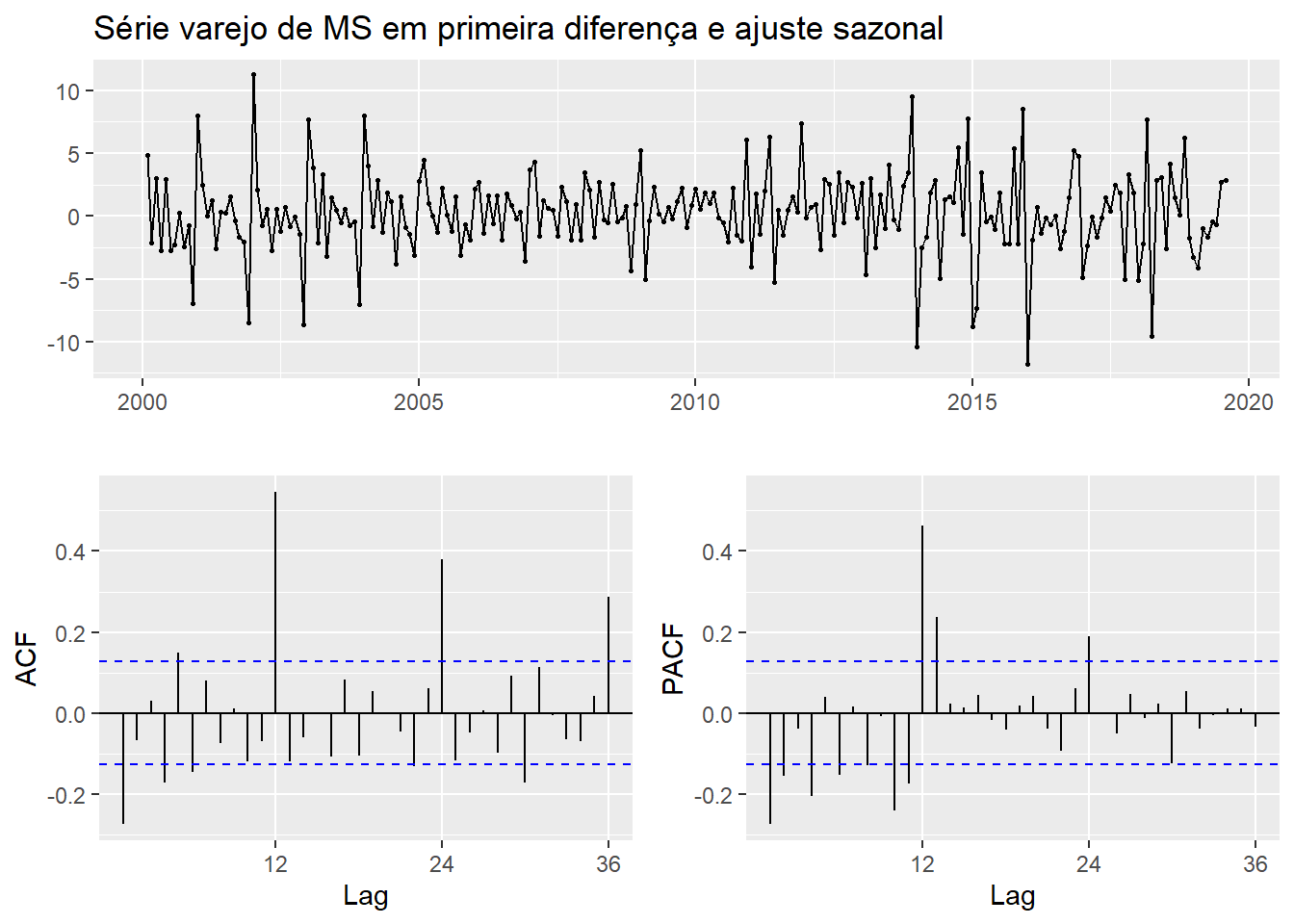

Método Theta pelo forecast::thetaf

y <- varejoms
h = 12
require(forecast)
T <- thetaf(y, h)$mean
autoplot(varejoms, series = "Varejo-MS") + autolayer(T, series = "Theta", PI = FALSE) + 
    xlab("Mês/Ano") + ylab("Índice (2011=100)") + ggtitle("Índice de volume de vendas no varejo total de Mato Grosso do Sul <br> (Mensal) - BCB 1479")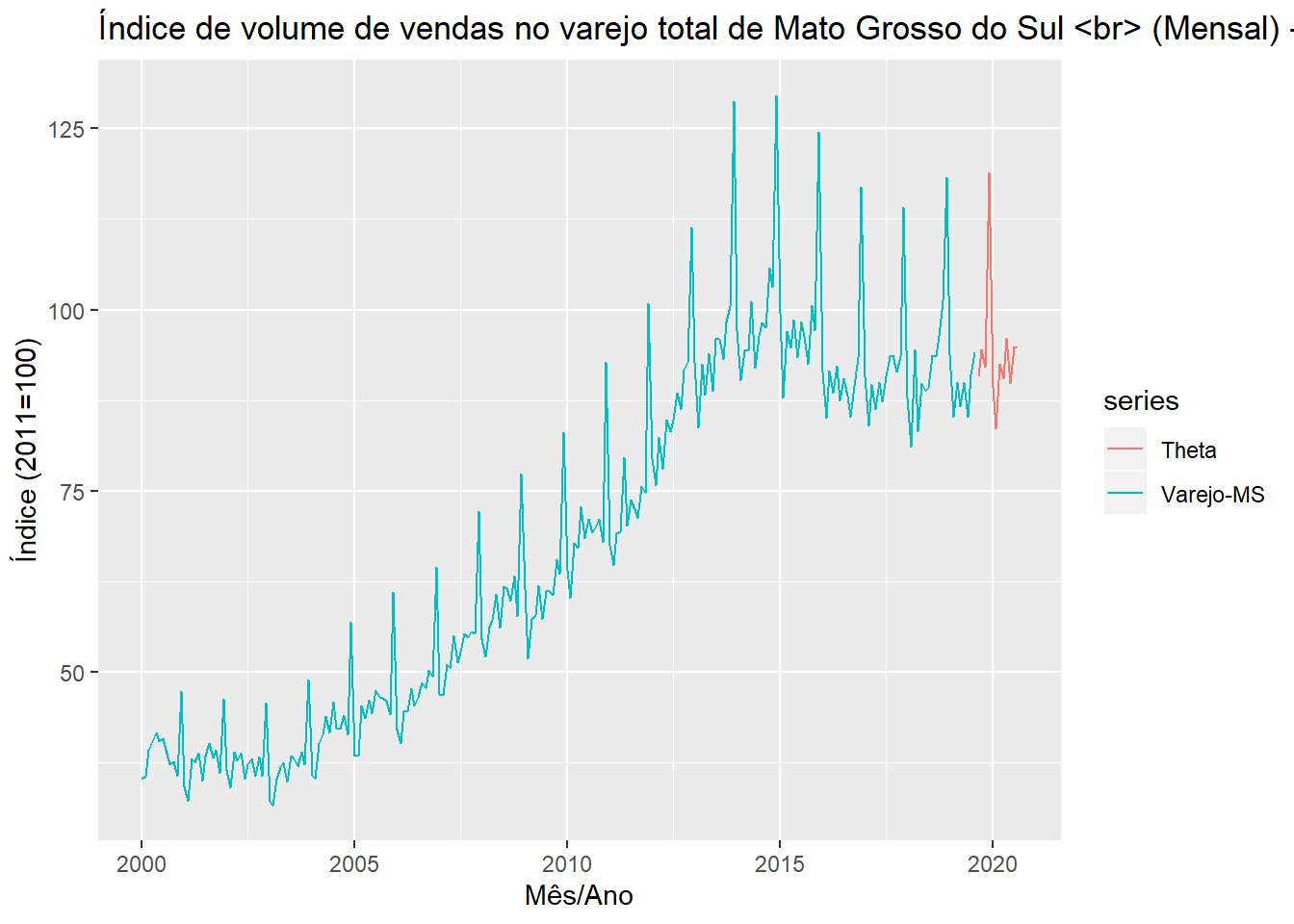

Ou pelo dygraphs, teremos:

library(dygraphs)
dygraph(cbind(varejoms, T), main = "Índice de volume de vendas no varejo total de Mato Grosso do Sul <br> (Mensal)  (2011=100) BCB 1479") %>% 
    dyAxis("x", drawGrid = TRUE) %>% dyEvent("2005-1-01", "2005", labelLoc = "bottom") %>% 
    dyEvent("2015-1-01", "2015", labelLoc = "bottom") %>% dyEvent("2018-1-01", "2018", 
    labelLoc = "bottom") %>% dyEvent("2019-1-01", "2019", labelLoc = "bottom") %>% 
    dyOptions(drawPoints = TRUE, pointSize = 2)

Outros detalhes estão no objeto Theta.

modelo <- thetaf(y, h)
summary(modelo)

Forecast method: Theta

Model Information:
$alpha
[1] 0.6379929

$drift
        X 
0.1636578 

$sigma
[1] 5.651715

$call
thetaf(y = y, h = h)


Error measures:
                    ME     RMSE      MAE       MPE     MAPE      MASE
Training set 0.3545975 2.389965 1.818344 0.5126286 2.748774 0.3983852
                    ACF1
Training set -0.09309372

Forecasts:
         Point Forecast     Lo 80     Hi 80     Lo 95     Hi 95
Sep 2019       90.76717  87.72049  93.81384  86.10768  95.42666
Oct 2019       94.53450  90.92057  98.14842  89.00748 100.06151
Nov 2019       92.07228  87.96879  96.17577  85.79654  98.34802
Dec 2019      118.91229 114.37172 123.45287 111.96808 125.85650
Jan 2020       89.33067  84.39154  94.26980  81.77692  96.88442
Feb 2020       83.61381  78.30597  88.92165  75.49616  91.73146
Mar 2020       92.45136  86.79880  98.10392  83.80652 101.09620
Apr 2020       90.56873  84.59130  96.54615  81.42705  99.71041
May 2020       96.09921  89.81369 102.38473  86.48634 105.71209
Jun 2020       89.79625  83.21704  96.37546  79.73422  99.85828
Jul 2020       94.82093  87.96059 101.68126  84.32895 105.31290
Aug 2020       94.79960  87.66922 101.92999  83.89462 105.70458
autoplot(modelo, PI = TRUE)

knitr::kable(modelo)
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Sep 2019 90.76717 87.72049 93.81384 86.10768 95.42666
Oct 2019 94.53450 90.92057 98.14842 89.00748 100.06151
Nov 2019 92.07228 87.96879 96.17577 85.79654 98.34802
Dec 2019 118.91229 114.37172 123.45287 111.96808 125.85650
Jan 2020 89.33067 84.39154 94.26980 81.77692 96.88442
Feb 2020 83.61381 78.30597 88.92165 75.49616 91.73146
Mar 2020 92.45136 86.79880 98.10392 83.80652 101.09620
Apr 2020 90.56873 84.59130 96.54615 81.42705 99.71041
May 2020 96.09921 89.81369 102.38473 86.48634 105.71209
Jun 2020 89.79625 83.21704 96.37546 79.73422 99.85828
Jul 2020 94.82093 87.96059 101.68126 84.32895 105.31290
Aug 2020 94.79960 87.66922 101.92999 83.89462 105.70458

Método Theta pelo forecTheta de Fiorucci et al (2016)

library(forecTheta)
y <- varejoms
h = 12
set.seed(12345)
mod2 <- dotm(y, h)
plot(mod2)

(mod2)
Forecast method: Dynamic Optimised Theta Model 

Seasonal decomposition type: multiplicative 

Optimisation method: Nelder-Mead 

Number of theta lines: 2 

Weights for theta lines:
        Estimative
omega_1       0.48
omega_2       0.52

Estimative of parameters:
        MLE
ell0  15.61
alpha  0.62
theta  1.92

Forecasting points and prediction intervals
             Mean    Lo 80    Hi 80    Lo 90    Hi 90    Lo 95    Hi 95
Sep 2019  90.7055  87.7358  94.3555  87.0361  95.0432  86.5322  95.7098
Oct 2019  94.4625  91.2530  98.5915  90.4380  99.4901  89.5612 100.3729
Nov 2019  91.9939  87.9531  96.3013  87.0091  97.6981  86.1153  98.2929
Dec 2019 118.7997 113.5964 125.0013 112.1571 126.6257 111.3828 127.9087
Jan 2020  89.2369  84.7963  94.2359  83.4705  95.0678  82.5591  96.2033
Feb 2020  83.5169  78.5097  88.5590  77.4747  89.7529  76.9382  91.4349
Mar 2020  92.3336  86.7244  98.2125  85.8621  99.3112  83.9983 100.0960
Apr 2020  90.4424  85.1185  96.1328  83.1143  97.9635  82.2356  98.6804
May 2020  95.9529  89.7126 102.5335  88.8577 103.9769  85.8770 104.7699
Jun 2020  89.6476  83.1236  96.1505  81.8708  97.2885  80.7374  98.5336
Jul 2020  94.6507  87.0673 101.6476  85.5549 103.3302  84.9208 104.3466
Aug 2020  94.6157  86.7363 101.6285  85.6061 103.3821  85.0348 104.6449

Warning: According with the Shapiro-Wilk test with 97% of confidence, the unseasoned residuals do not follow the Normal distribution. The prediction intervals may not be adequate.

Ou pelo dygraphs, teremos:

library(dygraphs)
require(forecast)
set.seed(12345)
T2 <- dotm(y, h)$mean
dygraph(cbind(varejoms, T2), main = "Índice de volume de vendas no varejo total de Mato Grosso do Sul <br> (Mensal)  (2011=100) BCB 1479") %>% 
    dyAxis("x", drawGrid = TRUE) %>% dyEvent("2005-1-01", "2005", labelLoc = "bottom") %>% 
    dyEvent("2015-1-01", "2015", labelLoc = "bottom") %>% dyEvent("2018-1-01", "2018", 
    labelLoc = "bottom") %>% dyEvent("2019-1-01", "2019", labelLoc = "bottom") %>% 
    dyOptions(drawPoints = TRUE, pointSize = 2)

Parâmetro theta estimado:

mod2$par[2]  # alpha
[1] 0.6234402
mod2$par[3]  # theta
[1] 1.921107

Pesos estimados:

mod2$weights
        Estimative
omega_1  0.4794667
omega_2  0.5205333

Valores iniciais dos thetas: 0,5 e 2. Opções para Método de otimização: ‘Nelder-Mead’, ‘L-BFGS-B’, ‘SANN’. O padrão é ‘Nelder-Mead’.

mod2$opt.method
[1] "Nelder-Mead"

Comparação com dados recentes

Agora que já temos as informações até fev/2020, podemos comparar as estimativas com os dados reais. Faremos a comparação relativamente ao forecast do forecast::thetaf.

# dadosnovos<-BETS::BETSget(1479)
dadosnovos <- structure(c(35.2, 35.6, 39.2, 40.5, 41.6, 40.4, 40.8, 38.7, 37.3, 37.6, 
    35.6, 47.4, 34.2, 32.2, 38, 37.5, 38.8, 35, 38.4, 40.2, 38.2, 39.3, 36, 46.3, 
    36.4, 34, 39, 37.8, 38.9, 35.3, 37.2, 38.1, 35.6, 38.3, 35.6, 45.7, 32.2, 31.6, 
    35.2, 36.8, 37.5, 34.8, 38.4, 38.1, 37, 39, 37.3, 49, 35.8, 35.3, 40.2, 41.3, 
    43.9, 41.6, 45.9, 42.3, 42.2, 44, 41.3, 56.9, 38.5, 38.5, 45.3, 43.6, 46.2, 44.3, 
    47.5, 46.5, 46.4, 46, 44.1, 61, 42, 40.2, 44.6, 44.5, 47.8, 45.3, 46.5, 48.5, 
    47.7, 50.2, 49.3, 64.5, 47, 46.8, 51, 50.5, 55, 51.3, 52.8, 55.3, 54.8, 55.6, 
    55.3, 72.2, 54.5, 52.1, 56.2, 57.2, 60.8, 56.1, 61.8, 61.6, 59.8, 63.3, 57.7, 
    77.4, 61.4, 51.9, 57.3, 57.9, 61.9, 57.3, 61.1, 61.1, 60.6, 65.6, 63.5, 83.1, 
    64.1, 60.2, 67.8, 67.1, 72.8, 68.5, 71.1, 69.3, 69.9, 71.1, 67.9, 92.7, 67.5, 
    64.8, 69.1, 69.4, 79.6, 70.2, 73.8, 72.5, 71.3, 75.6, 74.7, 100.8, 79.5, 75.7, 
    82.4, 78, 84.8, 83.2, 84.8, 88.5, 86.3, 91.7, 92.8, 111.4, 92.8, 83.7, 92.5, 
    88.3, 93.9, 88.8, 96, 95.9, 93.2, 98.3, 100.5, 128.8, 97.2, 90.2, 94.3, 94.4, 
    101.1, 92, 96.4, 98.2, 97.6, 105.8, 103.1, 129.6, 99.6, 87.8, 97, 94.8, 98.6, 
    93.4, 98.4, 96.4, 92.5, 100.6, 97.2, 124.5, 91.5, 85.1, 91.6, 88.5, 92.2, 87.4, 
    90.5, 88.1, 85.2, 89.4, 93.4, 116.9, 90.8, 84, 89.7, 86.3, 90, 87.3, 90.8, 93.5, 
    93.7, 91.4, 93.5, 114.1, 87.8, 81.1, 94.5, 83.2, 89.9, 88.8, 89.3, 93.7, 93.5, 
    96.3, 101.3, 118.3, 93.8, 85.2, 90, 86.6, 90, 85.2, 91, 94.4, 93.4, 95.9, 102.6, 
    116, 94.9, 89.1), .Tsp = c(2000, 2020.08333333333, 12), class = "ts")
# View(cbind.zoo(data.fcst,dadosnovos))
require(zoo)
print(cbind.zoo(T, dadosnovos)[230:242])
                 T dadosnovos
fev 2019        NA       85.2
mar 2019        NA       90.0
abr 2019        NA       86.6
mai 2019        NA       90.0
jun 2019        NA       85.2
jul 2019        NA       91.0
ago 2019        NA       94.4
set 2019  90.76717       93.4
out 2019  94.53450       95.9
nov 2019  92.07228      102.6
dez 2019 118.91229      116.0
jan 2020  89.33067       94.9
fev 2020  83.61381       89.1

Acurácia do período Setembro/2019 a fev/2020:

# pelo forecast::thetaf T <- thetaf(y, h)$mean
previsto <- T
observado <- dadosnovos[237:242]
forecast::accuracy(previsto, observado)
               ME     RMSE      MAE      MPE     MAPE
Test set 3.778214 5.615847 4.748978 4.003178 4.840044

Ou seja, um erro percentual médio de \(4.00\)% e um erro absoluto médio de \(\approx4.75\)%.

Comparação com o forecTheta::dotm

As estimativas para o forecTheta::dotm foram obtidas fazendo T2<- dotm(y,h)$mean. Da mesma forma, obtemos a acurácia do período Setembro/2019 a fev/2020.

# pelo forecTheta::dotm T2<- dotm(y,h)$mean
previsto2 <- T2
observado <- dadosnovos[237:242]
forecast::accuracy(previsto2, observado)
               ME     RMSE      MAE      MPE     MAPE
Test set 3.864104 5.670028 4.797325 4.090202 4.894704

Ou seja, um erro percentual médio de \(4.09\)% e um erro absoluto médio de \(\approx4.80\)%.

Referências

ASSIMAKOPOULOS, V. and NIKOLOPOULOS, K. (2000). The theta model: a decomposition approach to forecasting. International Journal of Forecasting, 16, 521-530. DOI: https://doi.org/10.1016/S0169-2070(00)00066-2

FERREIRA, Pedro Costa; SPERANZA, Talitha; COSTA, Jonatha. (2018). BETS: Brazilian Economic Time Series. R package version 0.4.9. Disponível em: https://CRAN.R-project.org/package=BETS.

FIORUCCI, Jose Augusto; LOUZADA, Francisco Louzada; YIQI, Bao. (2016). forecTheta: Forecasting Time Series by Theta Models. R package version 2.2. Disponível em: https://CRAN.R-project.org/package=forecTheta.

HYNDMAN, Rob J. (2018a). fpp2: Data for “Forecasting: Principles and Practice” (2nd Edition). R package version 2.3. Disponível em: https://CRAN.R-project.org/package=fpp2.

HYNDMAN, R.J., & ATHANASOPOULOS, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. Disponível em: https://otexts.com/fpp2/. Accessed on 12 Set 2019.

econometria forecasts séries temporais Theta
Avatar
Adriano M R Figueiredo
Professor of Regional Economics and Econometrics

My research interests include regional economics, econometrics, sustainable public policies and agricultural economics.

Related