Economia Regional em R: Indicadores de análise de especialização regional - QL, CE, KSI, RDI, DIV, UBIQ
Licença
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0
Citação
Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional em R: Indicadores de análise de especialização regional - \(QL\), \(CE\), \(KSI\), \(RDI\), \(DIV\), \(UBIQ\). Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em https://rpubs.com/amrofi/regional_parte_2 e https://adrianofigueiredo.netlify.app/post/economia-regional-em-r-indicadores-de-analise-2/.
Script para reprodução (se utilizar, citar como acima)
Download 2020-04-29-economia-regional-em-r-indicadores-de-analise-2.RmdIntrodução
Este material é uma sequência ao conteúdo da primeira parte disponível em Figueiredo (2020b). Na primeira parte foram apresentados os indicadores de desigualdade. Agora falaremos dos indicadores de especialização regional, conforme cita Monastério (2011). Outras leituras úteis além deste autor, são Coutinho (2017) e Figueiredo (2019c). Utilizaremos os pacotes REAT de Wieland (2019); e EconGeo de Balland (2017, 2019), além de algumas funções próprias.
Indicadores de Especialização Regional
O objetivo desses indicadores é resumir os padrões espaciais da atividade econômica, tentando compreender como um setor está distribuído em um local ou região, ou ainda, quais os locais mais importantes para um setor. Existem vários indicadores (\(QL\), \(CE\), \(KSI\), \(RDI\), \(DIV\), \(UBIQ\) entre outros) para uma mesma variável (por ex.: do nível de atividade, emprego, produção etc). É importante ressaltar a necessidade de se avaliar e compreender a organização dos dados nas planilhas e nas variáveis ou objetos em um software, de modo a realizar os procedimentos corretamente.
A ideia básica deste arquivo é orientar os procedimentos para o cálculo dos indicadores de análise regional a saber:
- Quociente Locacional \(QL\)
- Coeficiente de Especialização \(CE\)
- Coeficiente de Especialização de Krugman \(KSI\)
- Índice de Diversidade Regional \(RDI\)
- Índice de Diversidade \(DIV\)
- Índice de Ubiqüidade \(UBIQ\)
Organização dos dados
Para os próximos indicadores, necessita-se dos dados de emprego por setor em cada município de MS. Desta forma, chama-se a planilha já preparada com os dados da base de informações RAIS do Ministério do Trabalho e Emprego do Brasil (MTE). Um meio de obter tais informações eletronicamente é pelo pacote raisr. Outra forma é pela página da Secretaria do Trabalho do Ministério da Economia (antigo Ministério do Trabalho e Emprego - MTE) http://pdet.mte.gov.br/.
A RAIS possui os dados para o final de cada ano (dezembro), portanto, os saldos de empregados ocupados. A CAGED apresenta outro tipo de informação, a de ligados e desligados, invés do saldo de pessoas ocupadas. Utilizaremos os dados da RAIS por vínculos, por Divisão CNAE 2.0 e por município. Outras agregações podem ser testadas, a critério do usuário. O procedimento recomendado é baixar os dados primeiro, organizar e depois chamar a planilha consolidada para o No site, só consegui essa extratificação para após 2006. Sugiro olhar o video ilustrativo em https://youtu.be/b93l_T3xhiA.
Quociente Locacional \(QL\)
O Quociente Locacional (QL) é uma medida que dá a informação de qual o setor mais representado no município (região de análise) quando comparado com o mesmo setor no estado (região de referência). Foi elaborado inicialmente por Haig (1928) e vem sendo muito utilizado em várias análises regionais e de localização industrial. Também chamado de Índice de Revealed Comparative Advantage (RCA – ou Vantagem comparativa revelada, VCR) seguindo Ballasa (1965), ou índice de Hoover-Balassa.
A expressão básica é:
\[
QL_{ki}=\left( {\frac{{\frac{{{E_{ki}}}}{E_i}}}{{\frac{{{E_k}}}{E}}}} \right)
\]
em que: \({E_{ki}}\) é o emprego no setor \(k\) na localidade de análise \(i\); \({E_i}\) é o emprego total na localidade de análise \(i\); \({E_k}\) é o emprego no setor \(k\) da localidade de referência; e \(E\) é o emprego total da localidade de referência.
A ideia é saber se na localidade de análise, a proporção do emprego do setor é maior ou menor que esta proporção no local de referência. Assim, se o resultado for maior que hum \(\left( {QL_{ki}}\gt 1\right)\), então diz-se que a localidade de análise é relativamente mais especializada nesse setor que a localidade de refência. De outro lado, valores menores que a unidade \(\left( {QL_{ki}}\lt 1\right)\) indicam que a localidade analisada tem representação menor deste setor do que a representação deste na localidade de referência.
A função REAT:::locq pode ser utilizada para realizar este cálculo de QL, mas só permite para um local e não para uma série. Desta forma, elaborou-se uma função QL para realizar o cálculo do setor e para todas as localidades de modo automatizado. Segue a função QL(e_ki, e_i, e_k, e) a ser utilizada, em que: e_ki é o emprego no setor \(k\) no município \(i\); e_i é o emprego total no município \(i\); e_k é o emprego no setor \(k\) do MS; e e é o emprego total do MS.
# chamar os dados para o QL, IHH, PR e ICN E<-sum(ei) # ei é o emprego total da
# regiao i, E é o emprego total MS Ek<-sum(eki) # Ek é o emprego total MS do
# setor k
QL <- function(e_ki, e_i, e_k, e) {
# if (e_ki > e_i) { return (NA) }
# if (e_k > e) { return (NA) }
# if (e_i > e) { return (NA) }
s_ki <- e_ki/e_i
s_i <- e_k/e
LQ <- s_ki/s_i
return(LQ)
}
# chamar dados de emprego
library(readxl)
dadosemprego <- read_excel("emprego.xlsx", sheet = "2006")
# View(dadosemprego) attach(dadosemprego)
ei <- rowSums(as.matrix(dadosemprego[, 2:88]))
E <- colSums(dadosemprego[, 89], dims = 1)
ei <- dadosemprego[, 89]
# ei é o emprego total da regiao i, E é o emprego total MS Ek é o emprego total
# MS do setor k
Ek <- t(colSums(dadosemprego[, 2:88], dims = 1))
# teste - divisao 1
ql.ms <- QL(dadosemprego$`ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL`, ei,
Ek[1, 1], E)
ql.ms Total Geral
1 0.5885943
2 2.3529584
3 0.8262805
4 0.8822858
5 1.2637334
6 1.2985383
7 1.9092714
8 0.4753689
9 0.9879424
10 0.8761921
11 1.0401673
12 0.5424961
13 0.8364130
14 1.3289886
15 1.5954022
16 0.8367661
17 0.8925487
18 0.6731297
19 0.6843459
20 1.2576270
21 1.5534681
22 0.8610384
23 0.5865701
24 1.5131407
25 2.2058608
26 0.8546693
27 0.6247939
28 0.6344731
29 1.5808544
30 1.4852178
31 2.5448897
32 0.5009117
33 0.8749706
34 1.1197010
35 2.3193849
36 1.3218915
37 1.1905414
38 0.9259678
39 1.0366051
40 1.1898294
41 1.1488521
42 1.0273243
43 2.5730655
44 1.3250931
45 1.0120171
46 1.6500574
47 1.2840273
48 2.8691370
49 0.8995683
50 0.5618607
51 1.2206324
52 0.9600342
53 0.5158767
54 1.6215692
55 0.7014554
56 0.4900194
57 2.0168215
58 NaN
59 0.5978855
60 2.2979930
61 1.3607819
62 0.9999897
63 1.3111352
64 0.4954135
65 0.4167490
66 1.9431336
67 0.8263557
68 1.1759888
69 1.0622074
70 0.4284303
71 1.3179046
72 1.5697461
73 0.5904868
74 0.3900750
75 1.7493119
76 2.4270873
77 0.8594391
78 0.3943292
79 1.9148783# agora tentar automatizar para todas as colunas QL <- function (e_ki, e_i, e_k,
# e)
QL.MS.2006 <- dadosemprego$Munic
for (k in 1:87) {
# retirando linha 80 e coluna 1
dadosemp2 <- dadosemprego[1:79, k + 1]
QL.2006 <- QL(dadosemp2, ei, Ek[1, k], E)
QL.MS.2006 <- cbind(QL.MS.2006, QL.2006)
}
QL.MS.2006[, 1:3] # pedi para sair apenas duas divisoes QL.MS.2006 ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL
1 MS-AGUA CLARA 0.5885943
2 MS-ALCINOPOLIS 2.3529584
3 MS-AMAMBAI 0.8262805
4 MS-ANASTACIO 0.8822858
5 MS-ANAURILANDIA 1.2637334
6 MS-ANGELICA 1.2985383
7 MS-ANTONIO JOAO 1.9092714
8 MS-APARECIDA DO TABOADO 0.4753689
9 MS-AQUIDAUANA 0.9879424
10 MS-ARAL MOREIRA 0.8761921
11 MS-BANDEIRANTES 1.0401673
12 MS-BATAGUASSU 0.5424961
13 MS-BATAYPORA 0.8364130
14 MS-BELA VISTA 1.3289886
15 MS-BODOQUENA 1.5954022
16 MS-BONITO 0.8367661
17 MS-BRASILANDIA 0.8925487
18 MS-CAARAPO 0.6731297
19 MS-CAMAPUA 0.6843459
20 MS-CAMPO GRANDE 1.2576270
21 MS-CARACOL 1.5534681
22 MS-CASSILANDIA 0.8610384
23 MS-CHAPADAO DO SUL 0.5865701
24 MS-CORGUINHO 1.5131407
25 MS-CORONEL SAPUCAIA 2.2058608
26 MS-CORUMBA 0.8546693
27 MS-COSTA RICA 0.6247939
28 MS-COXIM 0.6344731
29 MS-DEODAPOLIS 1.5808544
30 MS-DOIS IRMAOS DO BURITI 1.4852178
31 MS-DOURADINA 2.5448897
32 MS-DOURADOS 0.5009117
33 MS-ELDORADO 0.8749706
AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS
1 0.0000000
2 0.0000000
3 0.0000000
4 0.0000000
5 0.0000000
6 0.0000000
7 0.0000000
8 0.0000000
9 5.4161192
10 0.0000000
11 0.0000000
12 0.0000000
13 0.0000000
14 0.0000000
15 0.0000000
16 23.1868323
17 0.2788992
18 0.0000000
19 0.0000000
20 0.9923635
21 0.0000000
22 0.8042345
23 0.4957804
24 0.0000000
25 0.0000000
26 4.9645736
27 0.0000000
28 0.2880881
29 0.8085942
30 0.0000000
31 0.0000000
32 0.7293951
33 0.0000000
[ reached 'max' / getOption("max.print") -- omitted 46 rows ]O mesmo procedimento é mais facilmente obtido com uso do pacote EconGeo de Balland (2019). Outra opção é calcular no Excel. Maiores detalhes podem ser obtidos em Figueiredo (2020c)
Agora vamos recalcular para 2006 e 2016, com dados da RAIS no mesmo formato.
- Para 2006:
require(EconGeo)
library(readxl)
dadosemprego <- read_excel("emprego.xlsx", sheet = "2006")
nomes <- read_excel("emprego.xlsx", sheet = "nomes")
mat_0 <- as.matrix(dadosemprego[1:79, 2:88]) # 2006
rownames(mat_0) <- (dadosemprego$Munic)
class(mat_0) <- "numeric"
# considerando T0 para 20006 e T1 para 2016
QL_T0 <- as.data.frame(round(RCA(mat_0), digits = 4))
QL_T0 <- cbind(nomes, QL_T0)
# salvar data.frames para csv com write.csv() ou para excel
# writexl::write_xlsx(QL_T0,'qlms2006.xlsx')- Para 2016:
require(EconGeo)
library(readxl)
dadosemprego_1 <- read_excel("emprego.xlsx", sheet = "2016")
mat_1 <- as.matrix(dadosemprego_1[1:79, 2:88]) # 2016
rownames(mat_1) <- (dadosemprego_1$Munic)
class(mat_1) <- "numeric"
# considerando T0 para 20006 e T1 para 2016
QL_T1 <- as.data.frame(round(RCA(mat_1), digits = 4))
QL_T1 <- cbind(nomes, QL_T1)
# salvar data.frames para csv com write.csv() ou para excel
# writexl::write_xlsx(QL_T1,'qlms2016.xlsx')Mapa de QL para 2016
Para ver como elaborar mapas, ver Figueiredo (2019a;2020a). Utilizarei o pacote geobr para obter os arquivos básicos de mapas (shapes). Posso verificar que para MS, especificarei 50 e para o ano de 2016. Posso baixar os dados (shapes) para os municípios de Mato Grosso do Sul fazendo uso da função read_municipality(code_muni=50, year=2016) em:
Agora vou construir uma variável para ser plotada no mapa. Farei com o QL da divisão ‘Agricultura, pecuária e serviços relacionados’, 2016, a qual foi colocada dentro do objeto QL_T1_AGR. Preciso ter os meus dados em uma planilha em que uma das colunas será o código do município da mesma forma que consta em code_muni no objeto all_mun_ms. Recomendo fazer a associação entre os dados por meio do código, menos sujeito a erros de digitação que para os nomes dos municípios. Juntarei os datasets pela condição de que o code_muni do objeto all_mun_ms é igual ao code_muni do objeto QL_T1 todo.
library(dplyr)
library(ggplot2)
library(sf)
QL_T1_AGR <- QL_T1$`AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS`
dataset_T1 = left_join(all_mun_ms, QL_T1, by = c(code_muni = "code_muni"))
max(dataset_T1$`AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS`)[1] 6.1393min(dataset_T1$`AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS`)[1] 0.0527No mapa abaixo tem-se o QL da divisão Agricultura, pecuária e serviços relacionados em 2016, para Mato Grosso do Sul. É possível identificar que dez (10) entre os 79 municípios têm QL menores que 1 (\(QL\lt1\)). São eles: Campo Grande, Dourados, Três Lagoas, Coronel Sapucaia, Mundo Novo, Ladário, Bataguassu, Japorã, Angélica, Fátima do Sul.
library(ggplot2)
library("ggspatial")
ggplot() + geom_sf(data = dataset_T1, aes(fill = `AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS`),
color = NA, size = 0.15) + labs(title = "QL 2016 dos Municípios de MS para AGRIC",
caption = "Fonte: Elaboração própria", size = 8) + scale_fill_distiller(palette = "RdGy",
limits = c(0, 7), name = "QL_T1") + theme_minimal() + annotation_north_arrow(location = "bl",
which_north = "true", pad_x = unit(0.65, "in"), pad_y = unit(0.3, "in"), style = north_arrow_fancy_orienteering) +
annotation_scale(location = "bl", width_hint = 0.3)
Coeficiente de Especialização \(CE\)
O Coeficiente de especialização (\(CE\)) de Hoover e Giarratani (1984) faz uma análise alternativa ao indicador de quociente locacional, também para avaliar se o local é especializado em determinada atividade comparativamente ao local de referência. Para seu cálculo, recomenda-se utilizar os dados de emprego de cada local para cada setor, e comparar com os mesmos dados da economia de referência. Utiliza-se aqui a mesma notação utilizada no \(QL\), para a expressão de \(CE\) para a localidade \(i\):
\[ C{E_i} = \frac{1}{2}\sum\limits_k {\left| {\frac{{{E_{ki}}}}{{{E_i}}} - \frac{{{E_k}}}{E}} \right|} \]
em que: \({E_{ki}}\) é o emprego no setor \(k\) na localidade de análise \(i\); \({E_i}\) é o emprego total na localidade de análise \(i\); \({E_k}\) é o emprego no setor \(k\) da localidade de referência; e \(E\) é o emprego total da localidade de referência.
Valores próximos de zero (\(\left( {CE_{i}}= 0\right)\)) indicam que o local \(i\) tem estrutura no mesmo padrão de especialização que a localidade de referência. De forma oposta, valores próximos a hum (\(\left( {CE_{i}}= 1\right)\)) indicam que o local \(i\) tem padrão de especialização completamente diferente da localidade de referência.
O chunk abaixo é para um setor. É preciso fazer para cada setor e depois somar para todos os setores. Isto será finalizado, portanto, após o outro chunk.
# para um setor E<-sum(ei) # ei é o emprego total da regiao i, E é o emprego
# total MS Ek<-sum(eki) # Ek é o emprego total MS do setor k
CE <- function(e_ki, e_i, e_k, e) {
s_ki <- e_ki/e_i
s_i <- e_k/e
CEH <- 0.5 * abs(s_ki - s_i) # está fazendo para um setor apenas
return(CEH)
}
# chamar dados de emprego 2006
# dadosemprego <- read_excel('emprego.xlsx', sheet = '2006') View(dadosemprego)
# attach(dadosemprego) ei é o emprego total da regiao i
# ei<-rowSums(as.matrix(dadosemprego[,2:88])) # mas já coloquei o total geral no
# xlsx E é o emprego total MS
E <- colSums(dadosemprego[, 89], dims = 1)
ei <- dadosemprego[, 89]
# Ek é o emprego total MS do setor k
Ek <- t(colSums(dadosemprego[, 2:88], dims = 1))
# teste - divisao 1
ce.ms <- CE(dadosemprego$`ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL`, ei,
Ek[1, 1], E)Agora tentar automatizar para todas as colunas e ano de 2006. Reforço: o chunk acima é para um setor. É preciso fazer para cada setor e depois somar para todos os setores.
# agora tentar automatizar para todas as colunas e 2006 CE <- function (e_ki,
# e_i, e_k, e) QL <- function (e_ki, e_i, e_k, e)
CE.MS.2006 <- dadosemprego$Munic
for (k in 1:87) {
# retirando linha 80 e coluna 1
dadosemp2 <- dadosemprego[1:79, k + 1]
# CE.2006<- apply(X=dadosemp2,MARGIN=2,FUN = QL,e_i=ei, e_k=Ek,e=E)
CE.2006 <- CE(dadosemp2, ei, Ek[1, k], E)
CE.MS.2006 <- cbind(CE.MS.2006, CE.2006)
}
CE_2006 <- round(rowSums(as.matrix(CE.MS.2006[, 2:88])), 4)
knitr::kable(CE_2006)| x |
|---|
| 0.5157 |
| 0.5281 |
| 0.2452 |
| 0.3631 |
| 0.4226 |
| 0.4149 |
| 0.4833 |
| 0.3902 |
| 0.2356 |
| 0.4353 |
| 0.4465 |
| 0.4633 |
| 0.4341 |
| 0.3185 |
| 0.4322 |
| 0.3610 |
| 0.4321 |
| 0.3546 |
| 0.3997 |
| 0.1980 |
| 0.5116 |
| 0.2489 |
| 0.3602 |
| 0.4838 |
| 0.4493 |
| 0.2015 |
| 0.3806 |
| 0.3230 |
| 0.3234 |
| 0.4646 |
| 0.4997 |
| 0.2716 |
| 0.3361 |
| 0.2716 |
| 0.5189 |
| 0.2711 |
| 0.3042 |
| 0.3278 |
| 0.4082 |
| 0.3429 |
| 0.3266 |
| 0.2318 |
| 0.5609 |
| 0.4333 |
| 0.1997 |
| 0.5741 |
| 0.4683 |
| 0.6327 |
| 0.4610 |
| 0.3264 |
| 0.3223 |
| 0.3229 |
| 0.3700 |
| 0.3863 |
| 0.3993 |
| 0.3295 |
| 0.3888 |
| NaN |
| 0.2850 |
| 0.4824 |
| 0.3832 |
| 0.1591 |
| 0.4547 |
| 0.6003 |
| 0.4698 |
| 0.4428 |
| 0.3506 |
| 0.4689 |
| 0.5405 |
| 0.3259 |
| 0.4811 |
| 0.3282 |
| 0.4209 |
| 0.6030 |
| 0.4890 |
| 0.5084 |
| 0.4439 |
| 0.2918 |
| 0.4185 |
Esta rotina pode ser resumida fazendo o uso do pacote EconGeo, e a função spec.coeff. Ela utiliza uma matriz contendo os dados no formato abaixo, em que \((I1,I2,I3)\) são as indústrias ou setores, para os municípios \((R1,R2,R3)\).
| municipio | I1 | I2 | I3 |
|---|---|---|---|
| R1 | 100 | 150 | 165 |
| R2 | 130 | 400 | 220 |
| R3 | 200 | 1200 | 20 |
- Para 2006, usando a matriz mat_0, criada anteriormente: :
# Coeficiente de especialização de Hoover pelo EconGeo retorna exatamente o
# coeficiente (CE) visto anteriormente
library(EconGeo)
## gerar a matriz industrial da região, para T0=2006 para a matriz mat_0 criada
## anteriormente run the function
CE_T0 <- as.data.frame(round(spec.coeff(mat_0), digits = 4))
CE_T0 <- cbind(nomes, CE_T0)
colnames(CE_T0) <- c("code_muni", "nomemun", "CE_T0")
# salvar data.frames para csv com write.csv() ou para excel
# writexl::write_xlsx(CE_T0,'cems2006.xlsx')
knitr::kable(CE_T0)| code_muni | nomemun | CE_T0 | |
|---|---|---|---|
| MS-AGUA CLARA | 5000203 | Água Clara - MS | 0.5157 |
| MS-ALCINOPOLIS | 5000252 | Alcinópolis - MS | 0.5281 |
| MS-AMAMBAI | 5000609 | Amambai - MS | 0.2452 |
| MS-ANASTACIO | 5000708 | Anastácio - MS | 0.3631 |
| MS-ANAURILANDIA | 5000807 | Anaurilândia - MS | 0.4226 |
| MS-ANGELICA | 5000856 | Angélica - MS | 0.4149 |
| MS-ANTONIO JOAO | 5000906 | Antônio João - MS | 0.4833 |
| MS-APARECIDA DO TABOADO | 5001003 | Aparecida do Taboado - MS | 0.3902 |
| MS-AQUIDAUANA | 5001102 | Aquidauana - MS | 0.2356 |
| MS-ARAL MOREIRA | 5001243 | Aral Moreira - MS | 0.4353 |
| MS-BANDEIRANTES | 5001508 | Bandeirantes - MS | 0.4465 |
| MS-BATAGUASSU | 5001904 | Bataguassu - MS | 0.4633 |
| MS-BATAYPORA | 5002001 | Batayporã - MS | 0.4341 |
| MS-BELA VISTA | 5002100 | Bela Vista - MS | 0.3185 |
| MS-BODOQUENA | 5002159 | Bodoquena - MS | 0.4322 |
| MS-BONITO | 5002209 | Bonito - MS | 0.3610 |
| MS-BRASILANDIA | 5002308 | Brasilândia - MS | 0.4321 |
| MS-CAARAPO | 5002407 | Caarapó - MS | 0.3546 |
| MS-CAMAPUA | 5002605 | Camapuã - MS | 0.3997 |
| MS-CAMPO GRANDE | 5002704 | Campo Grande - MS | 0.1980 |
| MS-CARACOL | 5002803 | Caracol - MS | 0.5116 |
| MS-CASSILANDIA | 5002902 | Cassilândia - MS | 0.2489 |
| MS-CHAPADAO DO SUL | 5002951 | Chapadão do Sul - MS | 0.3602 |
| MS-CORGUINHO | 5003108 | Corguinho - MS | 0.4838 |
| MS-CORONEL SAPUCAIA | 5003157 | Coronel Sapucaia - MS | 0.4493 |
| MS-CORUMBA | 5003207 | Corumbá - MS | 0.2015 |
| MS-COSTA RICA | 5003256 | Costa Rica - MS | 0.3806 |
| MS-COXIM | 5003306 | Coxim - MS | 0.3230 |
| MS-DEODAPOLIS | 5003454 | Deodápolis - MS | 0.3234 |
| MS-DOIS IRMAOS DO BURITI | 5003488 | Dois Irmãos do Buriti - MS | 0.4646 |
| MS-DOURADINA | 5003504 | Douradina - MS | 0.4997 |
| MS-DOURADOS | 5003702 | Dourados - MS | 0.2716 |
| MS-ELDORADO | 5003751 | Eldorado - MS | 0.3361 |
| MS-FATIMA DO SUL | 5003801 | Fátima do Sul - MS | 0.2716 |
| MS-FIGUEIRAO | 5003900 | Figueirão - MS | 0.5189 |
| MS-GLORIA DE DOURADOS | 5004007 | Glória de Dourados - MS | 0.2711 |
| MS-GUIA LOPES DA LAGUNA | 5004106 | Guia Lopes da Laguna - MS | 0.3042 |
| MS-IGUATEMI | 5004304 | Iguatemi - MS | 0.3278 |
| MS-INOCENCIA | 5004403 | Inocência - MS | 0.4082 |
| MS-ITAPORA | 5004502 | Itaporã - MS | 0.3429 |
| MS-ITAQUIRAI | 5004601 | Itaquiraí - MS | 0.3266 |
| MS-IVINHEMA | 5004700 | Ivinhema - MS | 0.2318 |
| MS-JAPORA | 5004809 | Japorã - MS | 0.5609 |
| MS-JARAGUARI | 5004908 | Jaraguari - MS | 0.4333 |
| MS-JARDIM | 5005004 | Jardim - MS | 0.1997 |
| MS-JATEI | 5005103 | Jateí - MS | 0.5741 |
| MS-JUTI | 5005152 | Juti - MS | 0.4683 |
| MS-LADARIO | 5005202 | Ladário - MS | 0.6327 |
| MS-LAGUNA CARAPA | 5005251 | Laguna Carapã - MS | 0.4610 |
| MS-MARACAJU | 5005400 | Maracaju - MS | 0.3264 |
| MS-MIRANDA | 5005608 | Miranda - MS | 0.3223 |
| MS-MUNDO NOVO | 5005681 | Mundo Novo - MS | 0.3229 |
| MS-NAVIRAI | 5005707 | Naviraí - MS | 0.3700 |
| MS-NIOAQUE | 5005806 | Nioaque - MS | 0.3863 |
| MS-NOVA ALVORADA DO SUL | 5006002 | Nova Alvorada do Sul - MS | 0.3993 |
| MS-NOVA ANDRADINA | 5006200 | Nova Andradina - MS | 0.3295 |
| MS-NOVO HORIZONTE DO SUL | 5006259 | Novo Horizonte do Sul - MS | 0.3888 |
| MS-PARAISO DAS AGUAS | 5006275 | Paraíso das Águas - MS | NaN |
| MS-PARANAIBA | 5006309 | Paranaíba - MS | 0.2850 |
| MS-PARANHOS | 5006358 | Paranhos - MS | 0.4824 |
| MS-PEDRO GOMES | 5006408 | Pedro Gomes - MS | 0.3832 |
| MS-PONTA PORA | 5006606 | Ponta Porã - MS | 0.1591 |
| MS-PORTO MURTINHO | 5006903 | Porto Murtinho - MS | 0.4547 |
| MS-RIBAS DO RIO PARDO | 5007109 | Ribas do Rio Pardo - MS | 0.6003 |
| MS-RIO BRILHANTE | 5007208 | Rio Brilhante - MS | 0.4698 |
| MS-RIO NEGRO | 5007307 | Rio Negro - MS | 0.4428 |
| MS-RIO VERDE DE MATO GROSSO | 5007406 | Rio Verde de Mato Grosso - MS | 0.3506 |
| MS-ROCHEDO | 5007505 | Rochedo - MS | 0.4689 |
| MS-SANTA RITA DO PARDO | 5007554 | Santa Rita do Pardo - MS | 0.5405 |
| MS-SAO GABRIEL DO OESTE | 5007695 | São Gabriel do Oeste - MS | 0.3259 |
| MS-SELVIRIA | 5007802 | Selvíria - MS | 0.4811 |
| MS-SETE QUEDAS | 5007703 | Sete Quedas - MS | 0.3282 |
| MS-SIDROLANDIA | 5007901 | Sidrolândia - MS | 0.4209 |
| MS-SONORA | 5007935 | Sonora - MS | 0.6030 |
| MS-TACURU | 5007950 | Tacuru - MS | 0.4890 |
| MS-TAQUARUSSU | 5007976 | Taquarussu - MS | 0.5084 |
| MS-TERENOS | 5008008 | Terenos - MS | 0.4439 |
| MS-TRES LAGOAS | 5008305 | Três Lagoas - MS | 0.2918 |
| MS-VICENTINA | 5008404 | Vicentina - MS | 0.4185 |
- Para 2016, usando a matriz mat_1, criada anteriormente:
require(EconGeo)
library(readxl)
# considerando T0 para 20006 e T1 para 2016
CE_T1 <- as.data.frame(round(spec.coeff(mat_1), digits = 4))
CE_T1 <- cbind(nomes, CE_T1)
colnames(CE_T1) <- c("code_muni", "nomemun", "CE_T1")
# salvar data.frames para csv com write.csv() ou para excel
# writexl::write_xlsx(CE_T1,'cems2016.xlsx')
knitr::kable(CE_T1)| code_muni | nomemun | CE_T1 | |
|---|---|---|---|
| MS-AGUA CLARA | 5000203 | Água Clara - MS | 0.5772 |
| MS-ALCINOPOLIS | 5000252 | Alcinópolis - MS | 0.5627 |
| MS-AMAMBAI | 5000609 | Amambai - MS | 0.2312 |
| MS-ANASTACIO | 5000708 | Anastácio - MS | 0.4615 |
| MS-ANAURILANDIA | 5000807 | Anaurilândia - MS | 0.4398 |
| MS-ANGELICA | 5000856 | Angélica - MS | 0.7682 |
| MS-ANTONIO JOAO | 5000906 | Antônio João - MS | 0.5212 |
| MS-APARECIDA DO TABOADO | 5001003 | Aparecida do Taboado - MS | 0.4393 |
| MS-AQUIDAUANA | 5001102 | Aquidauana - MS | 0.2811 |
| MS-ARAL MOREIRA | 5001243 | Aral Moreira - MS | 0.4744 |
| MS-BANDEIRANTES | 5001508 | Bandeirantes - MS | 0.4282 |
| MS-BATAGUASSU | 5001904 | Bataguassu - MS | 0.4141 |
| MS-BATAYPORA | 5002001 | Batayporã - MS | 0.3852 |
| MS-BELA VISTA | 5002100 | Bela Vista - MS | 0.3901 |
| MS-BODOQUENA | 5002159 | Bodoquena - MS | 0.4941 |
| MS-BONITO | 5002209 | Bonito - MS | 0.4008 |
| MS-BRASILANDIA | 5002308 | Brasilândia - MS | 0.4639 |
| MS-CAARAPO | 5002407 | Caarapó - MS | 0.3579 |
| MS-CAMAPUA | 5002605 | Camapuã - MS | 0.3499 |
| MS-CAMPO GRANDE | 5002704 | Campo Grande - MS | 0.1900 |
| MS-CARACOL | 5002803 | Caracol - MS | 0.5811 |
| MS-CASSILANDIA | 5002902 | Cassilândia - MS | 0.2847 |
| MS-CHAPADAO DO SUL | 5002951 | Chapadão do Sul - MS | 0.3367 |
| MS-CORGUINHO | 5003108 | Corguinho - MS | 0.5722 |
| MS-CORONEL SAPUCAIA | 5003157 | Coronel Sapucaia - MS | 0.4153 |
| MS-CORUMBA | 5003207 | Corumbá - MS | 0.2426 |
| MS-COSTA RICA | 5003256 | Costa Rica - MS | 0.4267 |
| MS-COXIM | 5003306 | Coxim - MS | 0.2797 |
| MS-DEODAPOLIS | 5003454 | Deodápolis - MS | 0.3323 |
| MS-DOIS IRMAOS DO BURITI | 5003488 | Dois Irmãos do Buriti - MS | 0.4934 |
| MS-DOURADINA | 5003504 | Douradina - MS | 0.4316 |
| MS-DOURADOS | 5003702 | Dourados - MS | 0.2656 |
| MS-ELDORADO | 5003751 | Eldorado - MS | 0.2798 |
| MS-FATIMA DO SUL | 5003801 | Fátima do Sul - MS | 0.3251 |
| MS-FIGUEIRAO | 5003900 | Figueirão - MS | 0.5640 |
| MS-GLORIA DE DOURADOS | 5004007 | Glória de Dourados - MS | 0.3027 |
| MS-GUIA LOPES DA LAGUNA | 5004106 | Guia Lopes da Laguna - MS | 0.3983 |
| MS-IGUATEMI | 5004304 | Iguatemi - MS | 0.3286 |
| MS-INOCENCIA | 5004403 | Inocência - MS | 0.4468 |
| MS-ITAPORA | 5004502 | Itaporã - MS | 0.3832 |
| MS-ITAQUIRAI | 5004601 | Itaquiraí - MS | 0.4548 |
| MS-IVINHEMA | 5004700 | Ivinhema - MS | 0.2763 |
| MS-JAPORA | 5004809 | Japorã - MS | 0.6395 |
| MS-JARAGUARI | 5004908 | Jaraguari - MS | 0.5064 |
| MS-JARDIM | 5005004 | Jardim - MS | 0.2479 |
| MS-JATEI | 5005103 | Jateí - MS | 0.6099 |
| MS-JUTI | 5005152 | Juti - MS | 0.4653 |
| MS-LADARIO | 5005202 | Ladário - MS | 0.6171 |
| MS-LAGUNA CARAPA | 5005251 | Laguna Carapã - MS | 0.5526 |
| MS-MARACAJU | 5005400 | Maracaju - MS | 0.2785 |
| MS-MIRANDA | 5005608 | Miranda - MS | 0.3785 |
| MS-MUNDO NOVO | 5005681 | Mundo Novo - MS | 0.3125 |
| MS-NAVIRAI | 5005707 | Naviraí - MS | 0.2198 |
| MS-NIOAQUE | 5005806 | Nioaque - MS | 0.4310 |
| MS-NOVA ALVORADA DO SUL | 5006002 | Nova Alvorada do Sul - MS | 0.4490 |
| MS-NOVA ANDRADINA | 5006200 | Nova Andradina - MS | 0.2381 |
| MS-NOVO HORIZONTE DO SUL | 5006259 | Novo Horizonte do Sul - MS | 0.3679 |
| MS-PARAISO DAS AGUAS | 5006275 | Paraíso das Águas - MS | 0.5354 |
| MS-PARANAIBA | 5006309 | Paranaíba - MS | 0.3131 |
| MS-PARANHOS | 5006358 | Paranhos - MS | 0.4944 |
| MS-PEDRO GOMES | 5006408 | Pedro Gomes - MS | 0.4372 |
| MS-PONTA PORA | 5006606 | Ponta Porã - MS | 0.1949 |
| MS-PORTO MURTINHO | 5006903 | Porto Murtinho - MS | 0.5528 |
| MS-RIBAS DO RIO PARDO | 5007109 | Ribas do Rio Pardo - MS | 0.5936 |
| MS-RIO BRILHANTE | 5007208 | Rio Brilhante - MS | 0.4358 |
| MS-RIO NEGRO | 5007307 | Rio Negro - MS | 0.4569 |
| MS-RIO VERDE DE MATO GROSSO | 5007406 | Rio Verde de Mato Grosso - MS | 0.3518 |
| MS-ROCHEDO | 5007505 | Rochedo - MS | 0.5224 |
| MS-SANTA RITA DO PARDO | 5007554 | Santa Rita do Pardo - MS | 0.5895 |
| MS-SAO GABRIEL DO OESTE | 5007695 | São Gabriel do Oeste - MS | 0.3440 |
| MS-SELVIRIA | 5007802 | Selvíria - MS | 0.5973 |
| MS-SETE QUEDAS | 5007703 | Sete Quedas - MS | 0.3571 |
| MS-SIDROLANDIA | 5007901 | Sidrolândia - MS | 0.3364 |
| MS-SONORA | 5007935 | Sonora - MS | 0.4980 |
| MS-TACURU | 5007950 | Tacuru - MS | 0.4703 |
| MS-TAQUARUSSU | 5007976 | Taquarussu - MS | 0.6074 |
| MS-TERENOS | 5008008 | Terenos - MS | 0.4552 |
| MS-TRES LAGOAS | 5008305 | Três Lagoas - MS | 0.3702 |
| MS-VICENTINA | 5008404 | Vicentina - MS | 0.5127 |
Os resultados por essa rotina são exatamente os mesmos daqueles obtidos pela função do for-loop dos setores.
Mapa de CE para 2016
Agora vou construir o mapa para CE de 2016. Farei nova junção dos datasets pela condição de que o code_muni do objeto all_mun_ms é igual ao code_muni do objeto CE_T1 todo.
require(dplyr)
require(ggplot2)
require(sf)
dataset_CET1 = left_join(all_mun_ms, CE_T1, by = c(code_muni = "code_muni"))
max(dataset_CET1$CE_T1)[1] 0.7682min(dataset_CET1$CE_T1)[1] 0.19Portanto, o mapa pode ser feito conforme abaixo:
library(ggplot2)
library("ggspatial")
ggplot() + geom_sf(data = dataset_CET1, aes(fill = CE_T1), color = NA, size = 0.15) +
labs(title = "CE 2016 dos Municípios de MS", caption = "Fonte: Elaboração própria",
size = 8) + scale_fill_distiller(palette = "RdGy", limits = c(0.1, 0.8),
name = "CE_T1") + theme_minimal() + annotation_north_arrow(location = "bl", which_north = "true",
pad_x = unit(0.65, "in"), pad_y = unit(0.3, "in"), style = north_arrow_fancy_orienteering) +
annotation_scale(location = "bl", width_hint = 0.3)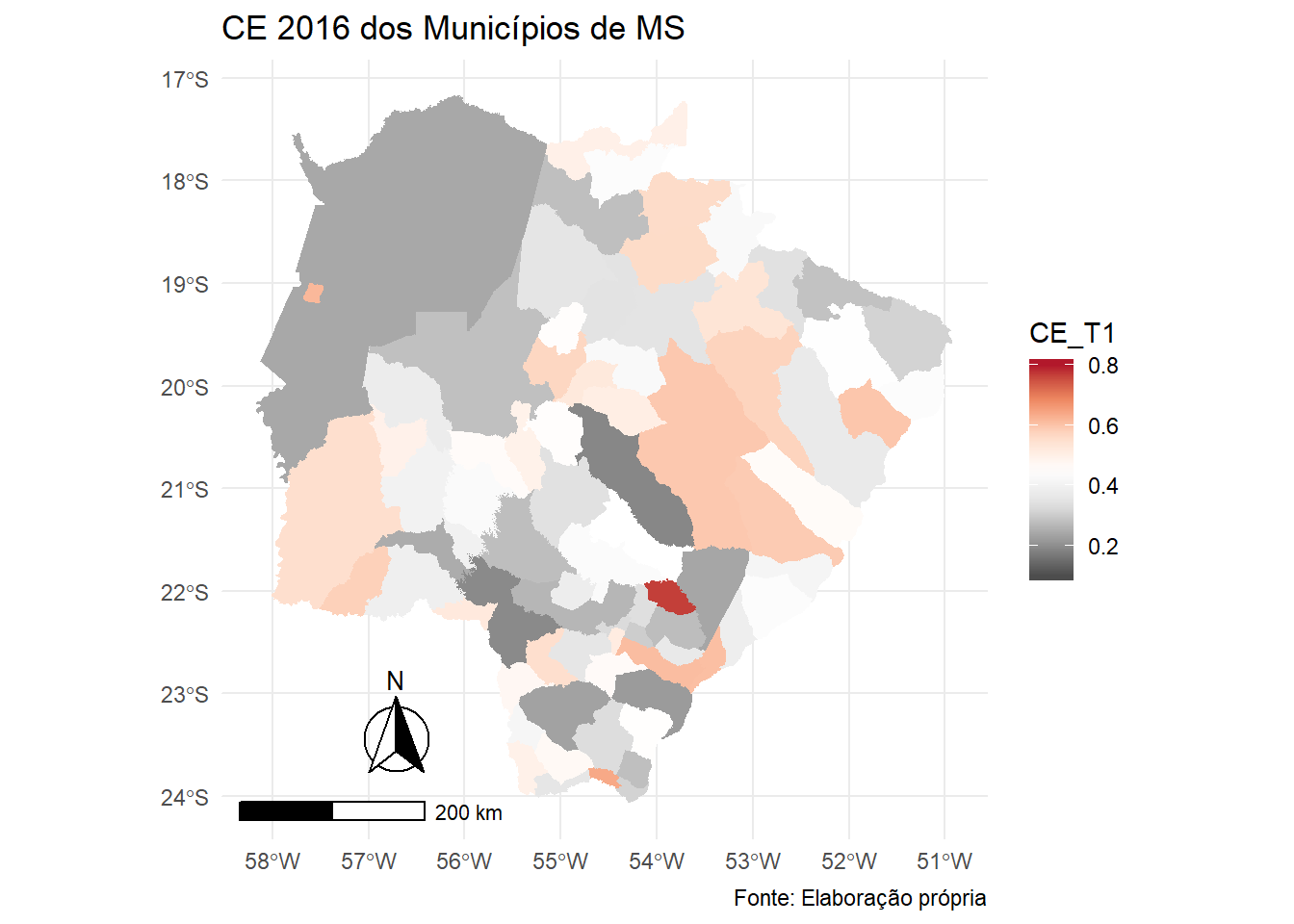
Assim, como exposto anteriormente, valores próximos de zero (\(\left( {CE_{i}}= 0\right)\)) indicam que o local \(i\) tem estrutura no mesmo padrão de especialização que a localidade de referência. De forma oposta, valores próximos a hum (\(\left( {CE_{i}}= 1\right)\)) indicam que o local \(i\) tem padrão de especialização completamente diferente da localidade de referência, neste caso, Angélica com 0.7682, o mais próximo de 1. Como era de esperar, os municípios mais populosos e com maiores economias estão mais próximos da referência que foi o estado de MS.
Coeficiente de Especialização de Krugman \(KSI\)
Baseado em Krugman (1991), esse indicador remete ao índice de Florence (1948) para comparações entre economias; neste caso, faz-se o município i e o estado j pela expressão:
\[
KS{I_{ij}} = \sum\limits_k {\left| {\frac{{{E_{ki}}}}{{{E_i}}} - \frac{{{E_{kj}}}}{{{E_j}}}} \right|}
\]
com \(0 \le KSI \le 2\) em que: \({E_{ki}}\) é o emprego no setor \(k\) na localidade de análise \(i\); \({E_i}\) é o emprego total na localidade de análise \(i\); \({E_k}\) é o emprego no setor \(k\) da localidade de referência \(j\); e \(E\) é o emprego total da localidade de referência \(j\).
Valores próximos de zero (\(\left( {KSI_{ij}}= 0\right)\)) indicam que o local \(i\) tem estrutura no mesmo padrão de especialização que a localidade de referência. De forma oposta, valores próximos a dois (\(\left( {KSI_{ij}}= 2\right)\)) indicam que o local \(i\) tem padrão de especialização completamente diferente da localidade de referência. Se dividido por 2, indica o mesmo que o \(CE_i\), ou o quanto da estrutura produtiva de uma localidade teria que ser modificada para ficar semelhante à de referência.
Para usar o pacote REAT, e a função krugman.spec, os dados devem estar no formato:
| setor | municipio | estado |
|---|---|---|
| A | 100 | 150 |
| B | 130 | 400 |
| C | 200 | 1200 |
Neste caso, o comando será krugman.spec(e_ij, e_il) sendo:
e_ij <- um vetor numérico com o emprego dos setores i na região j;
e_il <- um vetor numérico com o emprego dos setores i na região l.
require(REAT)
# os dados emprego estao com setores nas colunas e municipios nas linhas farei
# para campo grande e 2006
cg <- t(dadosemprego[20, 2:88])
KSI.ms <- krugman.spec(cg, Ek)
KSI.ms[1] 0.3959924# [1] 0.3959924 === dobro do CE!!!
# Calcularei agora para dourados
dour <- t(dadosemprego[32, 2:88])
KSId.ms <- krugman.spec(dour, Ek)
KSId.ms[1] 0.5432039# [1] 0.5432039 === dobro do CE!!!Agora, faz-se o mesmo cálculo de KSI para o conjunto de municípios de MS em 2006 com uso do pacote EconGeo e da função Krugman.index. Será necessário criar uma matriz com os dados desejados, no mesmo formato daquele utilizado para CE, ou seja:
Ela utiliza uma matriz contendo os dados no formato abaixo, em que \((I1,I2,I3)\) são as indústrias ou setores, para os municípios \((R1,R2,R3)\).
| municipio | I1 | I2 | I3 |
|---|---|---|---|
| R1 | 100 | 150 | 165 |
| R2 | 130 | 400 | 220 |
| R3 | 200 | 1200 | 20 |
# Coeficiente de especialização de Krugman pelo EconGeo
library(EconGeo)
# gerar a matriz industrial da região, para 2006 = mat_0, e para 2016 mat_1
KSI_T0 <- Krugman.index(mat_0)
KSI_T1 <- Krugman.index(mat_1)
KSI_T01 <- cbind(nomes, KSI_T0, KSI_T1)
knitr::kable(cbind(nomes, KSI_T0, KSI_T1), caption = "Coeficiente de especialização de Krugman em T0 e T1")| code_muni | nomemun | KSI_T0 | KSI_T1 | |
|---|---|---|---|---|
| MS-AGUA CLARA | 5000203 | Água Clara - MS | 1.0313222 | 1.1543561 |
| MS-ALCINOPOLIS | 5000252 | Alcinópolis - MS | 1.0562063 | 1.1253919 |
| MS-AMAMBAI | 5000609 | Amambai - MS | 0.4904486 | 0.4624966 |
| MS-ANASTACIO | 5000708 | Anastácio - MS | 0.7261549 | 0.9230223 |
| MS-ANAURILANDIA | 5000807 | Anaurilândia - MS | 0.8452346 | 0.8796183 |
| MS-ANGELICA | 5000856 | Angélica - MS | 0.8297766 | 1.5364524 |
| MS-ANTONIO JOAO | 5000906 | Antônio João - MS | 0.9666254 | 1.0424955 |
| MS-APARECIDA DO TABOADO | 5001003 | Aparecida do Taboado - MS | 0.7804670 | 0.8786323 |
| MS-AQUIDAUANA | 5001102 | Aquidauana - MS | 0.4712909 | 0.5621851 |
| MS-ARAL MOREIRA | 5001243 | Aral Moreira - MS | 0.8705765 | 0.9487009 |
| MS-BANDEIRANTES | 5001508 | Bandeirantes - MS | 0.8929240 | 0.8564239 |
| MS-BATAGUASSU | 5001904 | Bataguassu - MS | 0.9266342 | 0.8281359 |
| MS-BATAYPORA | 5002001 | Batayporã - MS | 0.8682910 | 0.7703697 |
| MS-BELA VISTA | 5002100 | Bela Vista - MS | 0.6370031 | 0.7802729 |
| MS-BODOQUENA | 5002159 | Bodoquena - MS | 0.8643566 | 0.9882960 |
| MS-BONITO | 5002209 | Bonito - MS | 0.7220436 | 0.8016098 |
| MS-BRASILANDIA | 5002308 | Brasilândia - MS | 0.8642086 | 0.9277429 |
| MS-CAARAPO | 5002407 | Caarapó - MS | 0.7092388 | 0.7158063 |
| MS-CAMAPUA | 5002605 | Camapuã - MS | 0.7994545 | 0.6997279 |
| MS-CAMPO GRANDE | 5002704 | Campo Grande - MS | 0.3959924 | 0.3799177 |
| MS-CARACOL | 5002803 | Caracol - MS | 1.0232159 | 1.1622012 |
| MS-CASSILANDIA | 5002902 | Cassilândia - MS | 0.4978322 | 0.5693333 |
| MS-CHAPADAO DO SUL | 5002951 | Chapadão do Sul - MS | 0.7204502 | 0.6733940 |
| MS-CORGUINHO | 5003108 | Corguinho - MS | 0.9675966 | 1.1443231 |
| MS-CORONEL SAPUCAIA | 5003157 | Coronel Sapucaia - MS | 0.8985673 | 0.8306262 |
| MS-CORUMBA | 5003207 | Corumbá - MS | 0.4029731 | 0.4852717 |
| MS-COSTA RICA | 5003256 | Costa Rica - MS | 0.7611764 | 0.8534383 |
| MS-COXIM | 5003306 | Coxim - MS | 0.6460918 | 0.5594908 |
| MS-DEODAPOLIS | 5003454 | Deodápolis - MS | 0.6467780 | 0.6645952 |
| MS-DOIS IRMAOS DO BURITI | 5003488 | Dois Irmãos do Buriti - MS | 0.9292158 | 0.9868331 |
| MS-DOURADINA | 5003504 | Douradina - MS | 0.9994499 | 0.8631833 |
| MS-DOURADOS | 5003702 | Dourados - MS | 0.5432039 | 0.5312308 |
| MS-ELDORADO | 5003751 | Eldorado - MS | 0.6721290 | 0.5596350 |
| MS-FATIMA DO SUL | 5003801 | Fátima do Sul - MS | 0.5432597 | 0.6501354 |
| MS-FIGUEIRAO | 5003900 | Figueirão - MS | 1.0378348 | 1.1279033 |
| MS-GLORIA DE DOURADOS | 5004007 | Glória de Dourados - MS | 0.5421902 | 0.6054133 |
| MS-GUIA LOPES DA LAGUNA | 5004106 | Guia Lopes da Laguna - MS | 0.6083970 | 0.7965077 |
| MS-IGUATEMI | 5004304 | Iguatemi - MS | 0.6556439 | 0.6572727 |
| MS-INOCENCIA | 5004403 | Inocência - MS | 0.8164594 | 0.8935795 |
| MS-ITAPORA | 5004502 | Itaporã - MS | 0.6858674 | 0.7664833 |
| MS-ITAQUIRAI | 5004601 | Itaquiraí - MS | 0.6531748 | 0.9096394 |
| MS-IVINHEMA | 5004700 | Ivinhema - MS | 0.4635360 | 0.5525029 |
| MS-JAPORA | 5004809 | Japorã - MS | 1.1217321 | 1.2789420 |
| MS-JARAGUARI | 5004908 | Jaraguari - MS | 0.8666906 | 1.0127292 |
| MS-JARDIM | 5005004 | Jardim - MS | 0.3993669 | 0.4958605 |
| MS-JATEI | 5005103 | Jateí - MS | 1.1481365 | 1.2197530 |
| MS-JUTI | 5005152 | Juti - MS | 0.9366298 | 0.9305649 |
| MS-LADARIO | 5005202 | Ladário - MS | 1.2653805 | 1.2342415 |
| MS-LAGUNA CARAPA | 5005251 | Laguna Carapã - MS | 0.9219031 | 1.1052264 |
| MS-MARACAJU | 5005400 | Maracaju - MS | 0.6528928 | 0.5569020 |
| MS-MIRANDA | 5005608 | Miranda - MS | 0.6445548 | 0.7570080 |
| MS-MUNDO NOVO | 5005681 | Mundo Novo - MS | 0.6457141 | 0.6249333 |
| MS-NAVIRAI | 5005707 | Naviraí - MS | 0.7400071 | 0.4396763 |
| MS-NIOAQUE | 5005806 | Nioaque - MS | 0.7726893 | 0.8620759 |
| MS-NOVA ALVORADA DO SUL | 5006002 | Nova Alvorada do Sul - MS | 0.7985827 | 0.8979549 |
| MS-NOVA ANDRADINA | 5006200 | Nova Andradina - MS | 0.6589728 | 0.4761331 |
| MS-NOVO HORIZONTE DO SUL | 5006259 | Novo Horizonte do Sul - MS | 0.7776049 | 0.7358660 |
| MS-PARAISO DAS AGUAS | 5006275 | Paraíso das Águas - MS | NaN | 1.0707292 |
| MS-PARANAIBA | 5006309 | Paranaíba - MS | 0.5700864 | 0.6261458 |
| MS-PARANHOS | 5006358 | Paranhos - MS | 0.9647376 | 0.9887275 |
| MS-PEDRO GOMES | 5006408 | Pedro Gomes - MS | 0.7663992 | 0.8743323 |
| MS-PONTA PORA | 5006606 | Ponta Porã - MS | 0.3182778 | 0.3897991 |
| MS-PORTO MURTINHO | 5006903 | Porto Murtinho - MS | 0.9094075 | 1.1055697 |
| MS-RIBAS DO RIO PARDO | 5007109 | Ribas do Rio Pardo - MS | 1.2005426 | 1.1871876 |
| MS-RIO BRILHANTE | 5007208 | Rio Brilhante - MS | 0.9395913 | 0.8715309 |
| MS-RIO NEGRO | 5007307 | Rio Negro - MS | 0.8856343 | 0.9137551 |
| MS-RIO VERDE DE MATO GROSSO | 5007406 | Rio Verde de Mato Grosso - MS | 0.7012308 | 0.7036328 |
| MS-ROCHEDO | 5007505 | Rochedo - MS | 0.9378026 | 1.0447059 |
| MS-SANTA RITA DO PARDO | 5007554 | Santa Rita do Pardo - MS | 1.0809941 | 1.1789131 |
| MS-SAO GABRIEL DO OESTE | 5007695 | São Gabriel do Oeste - MS | 0.6517082 | 0.6880806 |
| MS-SELVIRIA | 5007802 | Selvíria - MS | 0.9621806 | 1.1945557 |
| MS-SETE QUEDAS | 5007703 | Sete Quedas - MS | 0.6563678 | 0.7142198 |
| MS-SIDROLANDIA | 5007901 | Sidrolândia - MS | 0.8417860 | 0.6728008 |
| MS-SONORA | 5007935 | Sonora - MS | 1.2059139 | 0.9960949 |
| MS-TACURU | 5007950 | Tacuru - MS | 0.9779687 | 0.9406025 |
| MS-TAQUARUSSU | 5007976 | Taquarussu - MS | 1.0168512 | 1.2147462 |
| MS-TERENOS | 5008008 | Terenos - MS | 0.8878631 | 0.9104172 |
| MS-TRES LAGOAS | 5008305 | Três Lagoas - MS | 0.5836072 | 0.7404059 |
| MS-VICENTINA | 5008404 | Vicentina - MS | 0.8369777 | 1.0254396 |
# retorna exatamente o mesmo que anteriormente para campo grande e dourados, mas
# agora fez para todos os municípios de MSMapa de KSI para 2016
Agora vou construir o mapa para KSI de 2016. Farei nova junção dos datasets pela condição de que o code_muni do objeto all_mun_ms é igual ao code_muni do objeto KSI_T01 todo.
require(dplyr)
require(ggplot2)
require(sf)
dataset_KSIT1 = left_join(all_mun_ms, KSI_T01, by = c(code_muni = "code_muni"))
max(dataset_KSIT1$KSI_T1)[1] 1.536452min(dataset_KSIT1$KSI_T1)[1] 0.3799177Portanto, o mapa pode ser feito conforme abaixo:
library(ggplot2)
library("ggspatial")
ggplot() + geom_sf(data = dataset_KSIT1, aes(fill = KSI_T1), color = NA, size = 0.15) +
labs(title = "KSI 2016 dos Municípios de MS", caption = "Fonte: Elaboração própria",
size = 8) + scale_fill_distiller(palette = "RdGy", limits = c(0.3, 1.6),
name = "KSI_T1") + theme_minimal() + annotation_north_arrow(location = "bl",
which_north = "true", pad_x = unit(0.65, "in"), pad_y = unit(0.3, "in"), style = north_arrow_fancy_orienteering) +
annotation_scale(location = "bl", width_hint = 0.3)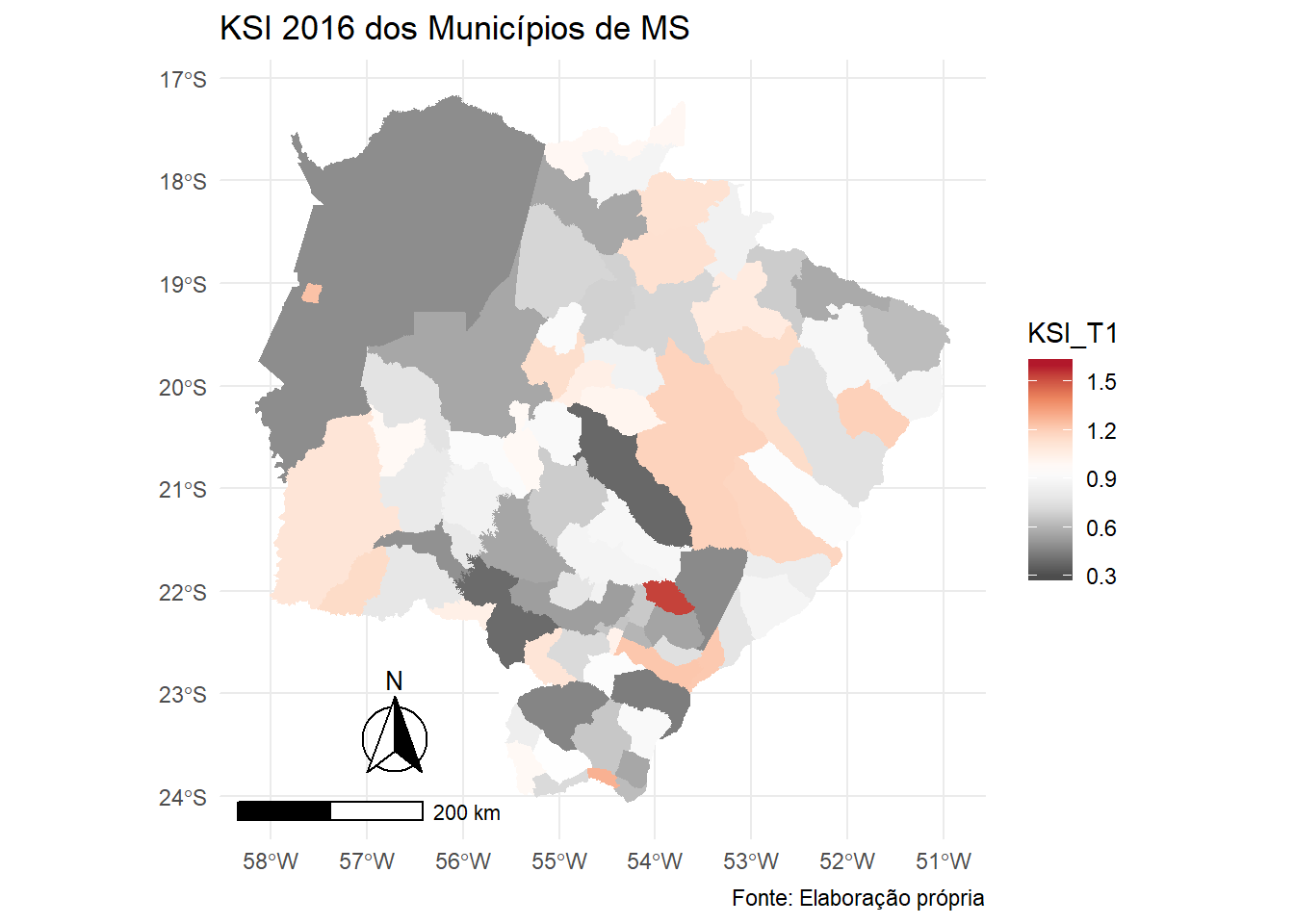
Valores próximos de zero (\(\left( {KSI_{ij}}= 0\right)\)) indicam que o local \(i\) tem estrutura no mesmo padrão de especialização que a localidade de referência. São os municípios indicados em tons de cinza. De forma oposta, valores próximos a dois (\(\left( {KSI_{ij}}= 2\right)\)) indicam que o local \(i\) tem padrão de especialização completamente diferente da localidade de referência, o caso dos tons quentes: laranja e avermelhados.
Índice de Diversidade Regional \(RDI\)
O Índice de Diversidade Industrial Regional (RDI, regional industrial diversity, ou Relative Diversity index - MCCANN, 2001, p.82), é o inverso do KSI.
# farei para campo grande e 2006
RDI.ms <- 1/KSI.ms
RDI.ms[1] 2.525301# Calcularei agora para dourados
RDId.ms <- 1/KSId.ms
RDId.ms[1] 1.840929Usando os objetos gerados no item anterior, para KSI_T0 e KSI_T1, tem-se:
RDI_T0 <- 1/KSI_T0
RDI_T1 <- 1/KSI_T1
RDI_T01 <- cbind(RDI_T0, RDI_T1)
knitr::kable(round(RDI_T01, digits = 4), caption = "Coeficiente de especialização de Krugman em T0 e T1")| RDI_T0 | RDI_T1 | |
|---|---|---|
| MS-AGUA CLARA | 0.9696 | 0.8663 |
| MS-ALCINOPOLIS | 0.9468 | 0.8886 |
| MS-AMAMBAI | 2.0389 | 2.1622 |
| MS-ANASTACIO | 1.3771 | 1.0834 |
| MS-ANAURILANDIA | 1.1831 | 1.1369 |
| MS-ANGELICA | 1.2051 | 0.6508 |
| MS-ANTONIO JOAO | 1.0345 | 0.9592 |
| MS-APARECIDA DO TABOADO | 1.2813 | 1.1381 |
| MS-AQUIDAUANA | 2.1218 | 1.7788 |
| MS-ARAL MOREIRA | 1.1487 | 1.0541 |
| MS-BANDEIRANTES | 1.1199 | 1.1676 |
| MS-BATAGUASSU | 1.0792 | 1.2075 |
| MS-BATAYPORA | 1.1517 | 1.2981 |
| MS-BELA VISTA | 1.5699 | 1.2816 |
| MS-BODOQUENA | 1.1569 | 1.0118 |
| MS-BONITO | 1.3850 | 1.2475 |
| MS-BRASILANDIA | 1.1571 | 1.0779 |
| MS-CAARAPO | 1.4100 | 1.3970 |
| MS-CAMAPUA | 1.2509 | 1.4291 |
| MS-CAMPO GRANDE | 2.5253 | 2.6321 |
| MS-CARACOL | 0.9773 | 0.8604 |
| MS-CASSILANDIA | 2.0087 | 1.7564 |
| MS-CHAPADAO DO SUL | 1.3880 | 1.4850 |
| MS-CORGUINHO | 1.0335 | 0.8739 |
| MS-CORONEL SAPUCAIA | 1.1129 | 1.2039 |
| MS-CORUMBA | 2.4816 | 2.0607 |
| MS-COSTA RICA | 1.3138 | 1.1717 |
| MS-COXIM | 1.5478 | 1.7873 |
| MS-DEODAPOLIS | 1.5461 | 1.5047 |
| MS-DOIS IRMAOS DO BURITI | 1.0762 | 1.0133 |
| MS-DOURADINA | 1.0006 | 1.1585 |
| MS-DOURADOS | 1.8409 | 1.8824 |
| MS-ELDORADO | 1.4878 | 1.7869 |
| MS-FATIMA DO SUL | 1.8407 | 1.5381 |
| MS-FIGUEIRAO | 0.9635 | 0.8866 |
| MS-GLORIA DE DOURADOS | 1.8444 | 1.6518 |
| MS-GUIA LOPES DA LAGUNA | 1.6437 | 1.2555 |
| MS-IGUATEMI | 1.5252 | 1.5214 |
| MS-INOCENCIA | 1.2248 | 1.1191 |
| MS-ITAPORA | 1.4580 | 1.3047 |
| MS-ITAQUIRAI | 1.5310 | 1.0993 |
| MS-IVINHEMA | 2.1573 | 1.8099 |
| MS-JAPORA | 0.8915 | 0.7819 |
| MS-JARAGUARI | 1.1538 | 0.9874 |
| MS-JARDIM | 2.5040 | 2.0167 |
| MS-JATEI | 0.8710 | 0.8198 |
| MS-JUTI | 1.0677 | 1.0746 |
| MS-LADARIO | 0.7903 | 0.8102 |
| MS-LAGUNA CARAPA | 1.0847 | 0.9048 |
| MS-MARACAJU | 1.5316 | 1.7956 |
| MS-MIRANDA | 1.5515 | 1.3210 |
| MS-MUNDO NOVO | 1.5487 | 1.6002 |
| MS-NAVIRAI | 1.3513 | 2.2744 |
| MS-NIOAQUE | 1.2942 | 1.1600 |
| MS-NOVA ALVORADA DO SUL | 1.2522 | 1.1136 |
| MS-NOVA ANDRADINA | 1.5175 | 2.1003 |
| MS-NOVO HORIZONTE DO SUL | 1.2860 | 1.3589 |
| MS-PARAISO DAS AGUAS | NaN | 0.9339 |
| MS-PARANAIBA | 1.7541 | 1.5971 |
| MS-PARANHOS | 1.0366 | 1.0114 |
| MS-PEDRO GOMES | 1.3048 | 1.1437 |
| MS-PONTA PORA | 3.1419 | 2.5654 |
| MS-PORTO MURTINHO | 1.0996 | 0.9045 |
| MS-RIBAS DO RIO PARDO | 0.8330 | 0.8423 |
| MS-RIO BRILHANTE | 1.0643 | 1.1474 |
| MS-RIO NEGRO | 1.1291 | 1.0944 |
| MS-RIO VERDE DE MATO GROSSO | 1.4261 | 1.4212 |
| MS-ROCHEDO | 1.0663 | 0.9572 |
| MS-SANTA RITA DO PARDO | 0.9251 | 0.8482 |
| MS-SAO GABRIEL DO OESTE | 1.5344 | 1.4533 |
| MS-SELVIRIA | 1.0393 | 0.8371 |
| MS-SETE QUEDAS | 1.5235 | 1.4001 |
| MS-SIDROLANDIA | 1.1880 | 1.4863 |
| MS-SONORA | 0.8292 | 1.0039 |
| MS-TACURU | 1.0225 | 1.0631 |
| MS-TAQUARUSSU | 0.9834 | 0.8232 |
| MS-TERENOS | 1.1263 | 1.0984 |
| MS-TRES LAGOAS | 1.7135 | 1.3506 |
| MS-VICENTINA | 1.1948 | 0.9752 |
Mapa de RDI para 2016
Agora vou construir o mapa para RDI de 2016. Farei nova junção dos datasets pela condição de que o code_muni do objeto all_mun_ms é igual ao code_muni do objeto RDI_T01 todo.
require(dplyr)
require(ggplot2)
require(sf)
RDI_T01 <- cbind(nomes, RDI_T0, RDI_T1)
dataset_RDIT1 = left_join(all_mun_ms, RDI_T01, by = c(code_muni = "code_muni"))
max(dataset_RDIT1$RDI_T1)[1] 2.632149min(dataset_RDIT1$RDI_T1)[1] 0.65085Portanto, o mapa pode ser feito conforme abaixo:
library(ggplot2)
library("ggspatial")
ggplot() + geom_sf(data = dataset_RDIT1, aes(fill = RDI_T1), color = NA, size = 0.15) +
labs(title = "RDI 2016 dos Municípios de MS", caption = "Fonte: Elaboração própria",
size = 8) + scale_fill_distiller(palette = "RdGy", limits = c(0.6, 2.7),
name = "RDI_T1") + theme_minimal() + annotation_north_arrow(location = "bl",
which_north = "true", pad_x = unit(0.65, "in"), pad_y = unit(0.3, "in"), style = north_arrow_fancy_orienteering) +
annotation_scale(location = "bl", width_hint = 0.3)
De forma oposta à especialização, os municípios com maiores RDI são os de menor KSI. Assim, nesse caso, os tons avermelhados são mais diversificados e os tons de cinza menos diversificados relativamente ao estado de MS.
Índice de Diversidade \(DIV\)
Cálculo da diversidade pelo pacote EconGeo, função diversity. A função calcula uma medida simples de diversidade das regiões calculando o número de setores nos quais a região tem vantagem comparativa relativa (RCA), ou seja, QL > 1 em relação as regiões das matrizes de incidência.
# gerar a matriz industrial da região, para 2006 = mat_0, e para 2016 mat_1
DIV_T0 <- diversity(mat_0, RCA = TRUE)
DIV_T1 <- diversity(mat_1, RCA = TRUE)
DIV_T01 <- cbind(DIV_T0, DIV_T1)
knitr::kable(round(DIV_T01, digits = 4), caption = "Índice de diversidade dos municípios de MS em T0 e T1")| DIV_T0 | DIV_T1 | |
|---|---|---|
| MS-AGUA CLARA | 8 | 9 |
| MS-ALCINOPOLIS | 5 | 7 |
| MS-AMAMBAI | 17 | 20 |
| MS-ANASTACIO | 9 | 15 |
| MS-ANAURILANDIA | 3 | 6 |
| MS-ANGELICA | 8 | 1 |
| MS-ANTONIO JOAO | 5 | 9 |
| MS-APARECIDA DO TABOADO | 19 | 21 |
| MS-AQUIDAUANA | 17 | 19 |
| MS-ARAL MOREIRA | 8 | 9 |
| MS-BANDEIRANTES | 10 | 9 |
| MS-BATAGUASSU | 9 | 9 |
| MS-BATAYPORA | 5 | 10 |
| MS-BELA VISTA | 8 | 10 |
| MS-BODOQUENA | 8 | 7 |
| MS-BONITO | 16 | 15 |
| MS-BRASILANDIA | 5 | 7 |
| MS-CAARAPO | 14 | 13 |
| MS-CAMAPUA | 8 | 10 |
| MS-CAMPO GRANDE | 54 | 51 |
| MS-CARACOL | 6 | 4 |
| MS-CASSILANDIA | 13 | 16 |
| MS-CHAPADAO DO SUL | 18 | 17 |
| MS-CORGUINHO | 12 | 10 |
| MS-CORONEL SAPUCAIA | 7 | 11 |
| MS-CORUMBA | 29 | 32 |
| MS-COSTA RICA | 13 | 10 |
| MS-COXIM | 16 | 18 |
| MS-DEODAPOLIS | 10 | 15 |
| MS-DOIS IRMAOS DO BURITI | 4 | 4 |
| MS-DOURADINA | 6 | 12 |
| MS-DOURADOS | 45 | 31 |
| MS-ELDORADO | 15 | 15 |
| MS-FATIMA DO SUL | 16 | 17 |
| MS-FIGUEIRAO | 5 | 4 |
| MS-GLORIA DE DOURADOS | 11 | 11 |
| MS-GUIA LOPES DA LAGUNA | 11 | 12 |
| MS-IGUATEMI | 6 | 11 |
| MS-INOCENCIA | 5 | 7 |
| MS-ITAPORA | 12 | 14 |
| MS-ITAQUIRAI | 8 | 5 |
| MS-IVINHEMA | 22 | 19 |
| MS-JAPORA | 4 | 4 |
| MS-JARAGUARI | 7 | 5 |
| MS-JARDIM | 24 | 20 |
| MS-JATEI | 3 | 4 |
| MS-JUTI | 3 | 5 |
| MS-LADARIO | 6 | 4 |
| MS-LAGUNA CARAPA | 7 | 5 |
| MS-MARACAJU | 20 | 14 |
| MS-MIRANDA | 14 | 12 |
| MS-MUNDO NOVO | 15 | 17 |
| MS-NAVIRAI | 14 | 28 |
| MS-NIOAQUE | 3 | 6 |
| MS-NOVA ALVORADA DO SUL | 9 | 6 |
| MS-NOVA ANDRADINA | 20 | 17 |
| MS-NOVO HORIZONTE DO SUL | 4 | 8 |
| MS-PARAISO DAS AGUAS | 0 | 6 |
| MS-PARANAIBA | 21 | 30 |
| MS-PARANHOS | 3 | 4 |
| MS-PEDRO GOMES | 9 | 10 |
| MS-PONTA PORA | 22 | 21 |
| MS-PORTO MURTINHO | 7 | 8 |
| MS-RIBAS DO RIO PARDO | 8 | 10 |
| MS-RIO BRILHANTE | 7 | 5 |
| MS-RIO NEGRO | 6 | 5 |
| MS-RIO VERDE DE MATO GROSSO | 12 | 9 |
| MS-ROCHEDO | 9 | 6 |
| MS-SANTA RITA DO PARDO | 3 | 4 |
| MS-SAO GABRIEL DO OESTE | 17 | 18 |
| MS-SELVIRIA | 10 | 7 |
| MS-SETE QUEDAS | 13 | 12 |
| MS-SIDROLANDIA | 7 | 9 |
| MS-SONORA | 7 | 9 |
| MS-TACURU | 2 | 6 |
| MS-TAQUARUSSU | 2 | 4 |
| MS-TERENOS | 12 | 12 |
| MS-TRES LAGOAS | 27 | 29 |
| MS-VICENTINA | 6 | 7 |
Mapa de Diversidade para 2016
Agora vou construir o mapa para DIV de 2016. Farei nova junção dos datasets pela condição de que o code_muni do objeto all_mun_ms é igual ao code_muni do objeto DIV_T01 todo.
require(dplyr)
require(ggplot2)
require(sf)
DIV_T01 <- cbind(nomes, DIV_T0, DIV_T1)
dataset_DIVT1 = left_join(all_mun_ms, DIV_T01, by = c(code_muni = "code_muni"))
max(dataset_DIVT1$DIV_T1)[1] 51min(dataset_DIVT1$DIV_T1)[1] 1Portanto, o mapa pode ser feito conforme abaixo:
library(ggplot2)
library("ggspatial")
ggplot() + geom_sf(data = dataset_DIVT1, aes(fill = DIV_T1), color = NA, size = 0.15) +
labs(title = "DIV 2016 dos Municípios de MS", caption = "Fonte: Elaboração própria",
size = 8) + scale_fill_distiller(palette = "RdGy", limits = c(0, 52), name = "DIV_T1") +
theme_minimal() + annotation_north_arrow(location = "bl", which_north = "true",
pad_x = unit(0.65, "in"), pad_y = unit(0.3, "in"), style = north_arrow_fancy_orienteering) +
annotation_scale(location = "bl", width_hint = 0.3)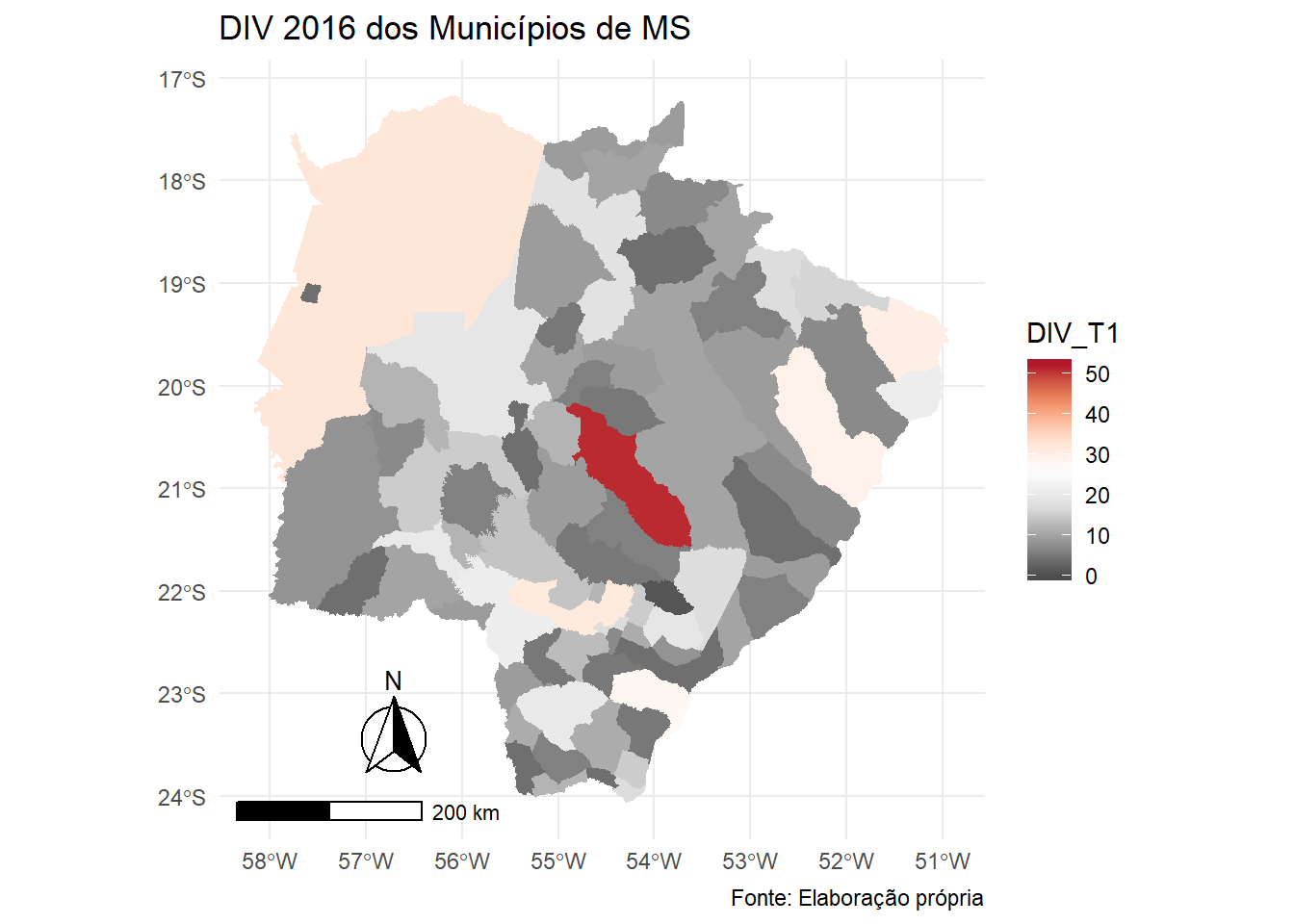
Neste caso, percebe-se que Campo Grande se destaca na diversidade, enquanto outros municípios em tons cinza estão com menso de 20 divisões CNAE cujo QL supera a unidade (\(QL\gt1\)).
Índice de Ubiqüidade \(UBIQ\)
A função ubiquity do pacote EconGeo calcula uma medida simples do número de regiões em que um setor é encontrado (ou seja, com QL>1). Teoricamente, setores que são mais comumente encontrados são setores menos complexos e, portanto, menos exigentes de capacidades técnicas.
UBIQ_T0 <- ubiquity(mat_0, RCA = TRUE) # 2006
UBIQ_T1 <- ubiquity(mat_1, RCA = TRUE) # 2016
UBIQ_T01 <- cbind(UBIQ_T0, UBIQ_T1)
knitr::kable(round(UBIQ_T01, digits = 4), caption = "Índice de Ubiqüidade dos municípios de MS em T0 e T1")| UBIQ_T0 | UBIQ_T1 | |
|---|---|---|
| ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL | 42 | 48 |
| AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS | 8 | 10 |
| AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS | 66 | 69 |
| ALIMENTAÇÃO | 17 | 14 |
| ALOJAMENTO | 19 | 22 |
| ALUGUÉIS NÃO-IMOBILIÁRIOS E GESTÃO DE ATIVOS INTANGÍVEIS NÃO-FINANCEIROS | 7 | 8 |
| ARMAZENAMENTO E ATIVIDADES AUXILIARES DOS TRANSPORTES | 19 | 19 |
| ATIVIDADES ARTÍSTICAS, CRIATIVAS E DE ESPETÁCULOS | 3 | 5 |
| ATIVIDADES AUXILIARES DOS SERVIÇOS FINANCEIROS, SEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 7 | 6 |
| ATIVIDADES CINEMATOGRÁFICAS, PRODUÇÃO DE VÍDEOS E DE PROGRAMAS DE TELEVISÃO | 8 | 4 |
| ATIVIDADES DE APOIO À EXTRAÇÃO DE MINERAIS | 2 | 2 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA | 6 | 7 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA INTEGRADAS COM ASSISTÊNCIA SOCIAL, PRESTADAS EM RESIDÊNCIAS COLETIVAS E PARTICULARES | 20 | 20 |
| ATIVIDADES DE EXPLORAÇÃO DE JOGOS DE AZAR E APOSTAS | 5 | 1 |
| ATIVIDADES DE ORGANIZAÇÕES ASSOCIATIVAS | 11 | 4 |
| ATIVIDADES DE PRESTAÇÃO DE SERVIÇOS DE INFORMAÇÃO | 11 | 10 |
| ATIVIDADES DE RÁDIO E DE TELEVISÃO | 18 | 16 |
| ATIVIDADES DE SEDES DE EMPRESAS E DE CONSULTORIA EM GESTÃO EMPRESARIAL | 2 | 6 |
| ATIVIDADES DE SERVIÇOS FINANCEIROS | 21 | 25 |
| ATIVIDADES DE VIGILÂNCIA, SEGURANÇA E INVESTIGAÇÃO | 3 | 5 |
| ATIVIDADES DOS SERVIÇOS DE TECNOLOGIA DA INFORMAÇÃO | 2 | 2 |
| ATIVIDADES ESPORTIVAS E DE RECREAÇÃO E LAZER | 13 | 12 |
| ATIVIDADES IMOBILIÁRIAS | 7 | 10 |
| ATIVIDADES JURÍDICAS, DE CONTABILIDADE E DE AUDITORIA | 32 | 34 |
| ATIVIDADES LIGADAS AO PATRIMÔNIO CULTURAL E AMBIENTAL | 3 | 4 |
| ATIVIDADES VETERINÁRIAS | 12 | 15 |
| CAPTAÇÃO, TRATAMENTO E DISTRIBUIÇÃO DE ÁGUA | 7 | 5 |
| COLETA, TRATAMENTO E DISPOSIÇÃO DE RESÍDUOS | 11 | 3 |
| COMÉRCIO E REPARAÇÃO DE VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 15 | 18 |
| COMÉRCIO POR ATACADO, EXCETO VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 22 | 24 |
| COMÉRCIO VAREJISTA | 27 | 34 |
| CONFECÇÃO DE ARTIGOS DO VESTUÁRIO E ACESSÓRIOS | 12 | 12 |
| CONSTRUÇÃO DE EDIFÍCIOS | 3 | 8 |
| CORREIO E OUTRAS ATIVIDADES DE ENTREGA | 20 | 21 |
| DESCONTAMINAÇÃO E OUTROS SERVIÇOS DE GESTÃO DE RESÍDUOS | 0 | 0 |
| EDIÇÃO E EDIÇÃO INTEGRADA À IMPRESSÃO | 6 | 7 |
| EDUCAÇÃO | 8 | 4 |
| ELETRICIDADE, GÁS E OUTRAS UTILIDADES | 13 | 22 |
| ESGOTO E ATIVIDADES RELACIONADAS | 6 | 3 |
| EXTRAÇÃO DE CARVÃO MINERAL | 12 | 0 |
| EXTRAÇÃO DE MINERAIS METÁLICOS | 1 | 1 |
| EXTRAÇÃO DE MINERAIS NÃO-METÁLICOS | 21 | 20 |
| EXTRAÇÃO DE PETRÓLEO E GÁS NATURAL | 1 | 0 |
| FABRICAÇÃO DE BEBIDAS | 3 | 4 |
| FABRICAÇÃO DE CELULOSE, PAPEL E PRODUTOS DE PAPEL | 5 | 2 |
| FABRICAÇÃO DE COQUE, DE PRODUTOS DERIVADOS DO PETRÓLEO E DE BIOCOMBUSTÍVEIS | 9 | 13 |
| FABRICAÇÃO DE EQUIPAMENTOS DE INFORMÁTICA, PRODUTOS ELETRÔNICOS E ÓPTICOS | 4 | 2 |
| FABRICAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 6 | 8 |
| FABRICAÇÃO DE MÁQUINAS, APARELHOS E MATERIAIS ELÉTRICOS | 3 | 4 |
| FABRICAÇÃO DE MÓVEIS | 14 | 12 |
| FABRICAÇÃO DE OUTROS EQUIPAMENTOS DE TRANSPORTE, EXCETO VEÍCULOS AUTOMOTORES | 5 | 4 |
| FABRICAÇÃO DE PRODUTOS ALIMENTÍCIOS | 25 | 24 |
| FABRICAÇÃO DE PRODUTOS DE BORRACHA E DE MATERIAL PLÁSTICO | 5 | 5 |
| FABRICAÇÃO DE PRODUTOS DE MADEIRA | 14 | 14 |
| FABRICAÇÃO DE PRODUTOS DE METAL, EXCETO MÁQUINAS E EQUIPAMENTOS | 10 | 13 |
| FABRICAÇÃO DE PRODUTOS DE MINERAIS NÃO-METÁLICOS | 22 | 24 |
| FABRICAÇÃO DE PRODUTOS DIVERSOS | 4 | 3 |
| FABRICAÇÃO DE PRODUTOS DO FUMO | 1 | 2 |
| FABRICAÇÃO DE PRODUTOS FARMOQUÍMICOS E FARMACÊUTICOS | 4 | 1 |
| FABRICAÇÃO DE PRODUTOS QUÍMICOS | 9 | 7 |
| FABRICAÇÃO DE PRODUTOS TÊXTEIS | 3 | 6 |
| FABRICAÇÃO DE VEÍCULOS AUTOMOTORES, REBOQUES E CARROCERIAS | 5 | 14 |
| IMPRESSÃO E REPRODUÇÃO DE GRAVAÇÕES | 10 | 14 |
| MANUTENÇÃO, REPARAÇÃO E INSTALAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 15 | 15 |
| METALURGIA | 5 | 7 |
| OBRAS DE INFRA-ESTRUTURA | 10 | 8 |
| ORGANISMOS INTERNACIONAIS E OUTRAS INSTITUIÇÕES EXTRATERRITORIAIS | 2 | 3 |
| OUTRAS ATIVIDADES DE SERVIÇOS PESSOAIS | 11 | 14 |
| OUTRAS ATIVIDADES PROFISSIONAIS, CIENTÍFICAS E TÉCNICAS | 11 | 13 |
| PESCA E AQÜICULTURA | 11 | 16 |
| PESQUISA E DESENVOLVIMENTO CIENTÍFICO | 4 | 4 |
| PREPARAÇÃO DE COUROS E FABRICAÇÃO DE ARTEFATOS DE COURO, ARTIGOS PARA VIAGEM E CALÇADOS | 6 | 7 |
| PRODUÇÃO FLORESTAL | 17 | 11 |
| PUBLICIDADE E PESQUISA DE MERCADO | 3 | 3 |
| REPARAÇÃO E MANUTENÇÃO DE EQUIPAMENTOS DE INFORMÁTICA E COMUNICAÇÃO E DE OBJETOS PESSOAIS E DOMÉSTICOS | 8 | 6 |
| SEGUROS, RESSEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 4 | 8 |
| SELEÇÃO, AGENCIAMENTO E LOCAÇÃO DE MÃO-DE-OBRA | 3 | 1 |
| SERVIÇOS DE ARQUITETURA E ENGENHARIA | 2 | 5 |
| SERVIÇOS DE ASSISTÊNCIA SOCIAL SEM ALOJAMENTO | 13 | 7 |
| SERVIÇOS DE ESCRITÓRIO, DE APOIO ADMINISTRATIVO E OUTROS SERVIÇOS PRESTADOS ÀS EMPRESAS | 4 | 2 |
| SERVIÇOS DOMÉSTICOS | 19 | 19 |
| SERVIÇOS ESPECIALIZADOS PARA CONSTRUÇÃO | 8 | 11 |
| SERVIÇOS PARA EDIFÍCIOS E ATIVIDADES PAISAGÍSTICAS | 2 | 4 |
| TELECOMUNICAÇÕES | 3 | 12 |
| TRANSPORTE AÉREO | 2 | 3 |
| TRANSPORTE AQUAVIÁRIO | 3 | 3 |
| TRANSPORTE TERRESTRE | 13 | 20 |
Nesse caso, as ubiqüidades são medidas por divisão CNAE e podemos verificar os valores ordenados. Ou seja, ranquear as divisões da maior para menor ubiqüidade. Os maiores valores são as divisões mais comuns nos municípios do estado de MS em 2016.
divisoes <- read_excel("emprego.xlsx", sheet = "divisoes", col_names = FALSE)
UBIQ_T01 <- cbind(divisoes, UBIQ_T0, UBIQ_T1)
rank.UBIQ <- UBIQ_T01[order(-UBIQ_T01$UBIQ_T1), ]
knitr::kable(rank.UBIQ[3:4])| UBIQ_T0 | UBIQ_T1 | |
|---|---|---|
| AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS | 66 | 69 |
| ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL | 42 | 48 |
| ATIVIDADES JURÍDICAS, DE CONTABILIDADE E DE AUDITORIA | 32 | 34 |
| COMÉRCIO VAREJISTA | 27 | 34 |
| ATIVIDADES DE SERVIÇOS FINANCEIROS | 21 | 25 |
| COMÉRCIO POR ATACADO, EXCETO VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 22 | 24 |
| FABRICAÇÃO DE PRODUTOS ALIMENTÍCIOS | 25 | 24 |
| FABRICAÇÃO DE PRODUTOS DE MINERAIS NÃO-METÁLICOS | 22 | 24 |
| ALOJAMENTO | 19 | 22 |
| ELETRICIDADE, GÁS E OUTRAS UTILIDADES | 13 | 22 |
| CORREIO E OUTRAS ATIVIDADES DE ENTREGA | 20 | 21 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA INTEGRADAS COM ASSISTÊNCIA SOCIAL, PRESTADAS EM RESIDÊNCIAS COLETIVAS E PARTICULARES | 20 | 20 |
| EXTRAÇÃO DE MINERAIS NÃO-METÁLICOS | 21 | 20 |
| TRANSPORTE TERRESTRE | 13 | 20 |
| ARMAZENAMENTO E ATIVIDADES AUXILIARES DOS TRANSPORTES | 19 | 19 |
| SERVIÇOS DOMÉSTICOS | 19 | 19 |
| COMÉRCIO E REPARAÇÃO DE VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 15 | 18 |
| ATIVIDADES DE RÁDIO E DE TELEVISÃO | 18 | 16 |
| PESCA E AQÜICULTURA | 11 | 16 |
| ATIVIDADES VETERINÁRIAS | 12 | 15 |
| MANUTENÇÃO, REPARAÇÃO E INSTALAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 15 | 15 |
| ALIMENTAÇÃO | 17 | 14 |
| FABRICAÇÃO DE PRODUTOS DE MADEIRA | 14 | 14 |
| FABRICAÇÃO DE VEÍCULOS AUTOMOTORES, REBOQUES E CARROCERIAS | 5 | 14 |
| IMPRESSÃO E REPRODUÇÃO DE GRAVAÇÕES | 10 | 14 |
| OUTRAS ATIVIDADES DE SERVIÇOS PESSOAIS | 11 | 14 |
| FABRICAÇÃO DE COQUE, DE PRODUTOS DERIVADOS DO PETRÓLEO E DE BIOCOMBUSTÍVEIS | 9 | 13 |
| FABRICAÇÃO DE PRODUTOS DE METAL, EXCETO MÁQUINAS E EQUIPAMENTOS | 10 | 13 |
| OUTRAS ATIVIDADES PROFISSIONAIS, CIENTÍFICAS E TÉCNICAS | 11 | 13 |
| ATIVIDADES ESPORTIVAS E DE RECREAÇÃO E LAZER | 13 | 12 |
| CONFECÇÃO DE ARTIGOS DO VESTUÁRIO E ACESSÓRIOS | 12 | 12 |
| FABRICAÇÃO DE MÓVEIS | 14 | 12 |
| TELECOMUNICAÇÕES | 3 | 12 |
| PRODUÇÃO FLORESTAL | 17 | 11 |
| SERVIÇOS ESPECIALIZADOS PARA CONSTRUÇÃO | 8 | 11 |
| AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS | 8 | 10 |
| ATIVIDADES DE PRESTAÇÃO DE SERVIÇOS DE INFORMAÇÃO | 11 | 10 |
| ATIVIDADES IMOBILIÁRIAS | 7 | 10 |
| ALUGUÉIS NÃO-IMOBILIÁRIOS E GESTÃO DE ATIVOS INTANGÍVEIS NÃO-FINANCEIROS | 7 | 8 |
| CONSTRUÇÃO DE EDIFÍCIOS | 3 | 8 |
| FABRICAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 6 | 8 |
| OBRAS DE INFRA-ESTRUTURA | 10 | 8 |
| SEGUROS, RESSEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 4 | 8 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA | 6 | 7 |
| EDIÇÃO E EDIÇÃO INTEGRADA À IMPRESSÃO | 6 | 7 |
| FABRICAÇÃO DE PRODUTOS QUÍMICOS | 9 | 7 |
| METALURGIA | 5 | 7 |
| PREPARAÇÃO DE COUROS E FABRICAÇÃO DE ARTEFATOS DE COURO, ARTIGOS PARA VIAGEM E CALÇADOS | 6 | 7 |
| SERVIÇOS DE ASSISTÊNCIA SOCIAL SEM ALOJAMENTO | 13 | 7 |
| ATIVIDADES AUXILIARES DOS SERVIÇOS FINANCEIROS, SEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 7 | 6 |
| ATIVIDADES DE SEDES DE EMPRESAS E DE CONSULTORIA EM GESTÃO EMPRESARIAL | 2 | 6 |
| FABRICAÇÃO DE PRODUTOS TÊXTEIS | 3 | 6 |
| REPARAÇÃO E MANUTENÇÃO DE EQUIPAMENTOS DE INFORMÁTICA E COMUNICAÇÃO E DE OBJETOS PESSOAIS E DOMÉSTICOS | 8 | 6 |
| ATIVIDADES ARTÍSTICAS, CRIATIVAS E DE ESPETÁCULOS | 3 | 5 |
| ATIVIDADES DE VIGILÂNCIA, SEGURANÇA E INVESTIGAÇÃO | 3 | 5 |
| CAPTAÇÃO, TRATAMENTO E DISTRIBUIÇÃO DE ÁGUA | 7 | 5 |
| FABRICAÇÃO DE PRODUTOS DE BORRACHA E DE MATERIAL PLÁSTICO | 5 | 5 |
| SERVIÇOS DE ARQUITETURA E ENGENHARIA | 2 | 5 |
| ATIVIDADES CINEMATOGRÁFICAS, PRODUÇÃO DE VÍDEOS E DE PROGRAMAS DE TELEVISÃO | 8 | 4 |
| ATIVIDADES DE ORGANIZAÇÕES ASSOCIATIVAS | 11 | 4 |
| ATIVIDADES LIGADAS AO PATRIMÔNIO CULTURAL E AMBIENTAL | 3 | 4 |
| EDUCAÇÃO | 8 | 4 |
| FABRICAÇÃO DE BEBIDAS | 3 | 4 |
| FABRICAÇÃO DE MÁQUINAS, APARELHOS E MATERIAIS ELÉTRICOS | 3 | 4 |
| FABRICAÇÃO DE OUTROS EQUIPAMENTOS DE TRANSPORTE, EXCETO VEÍCULOS AUTOMOTORES | 5 | 4 |
| PESQUISA E DESENVOLVIMENTO CIENTÍFICO | 4 | 4 |
| SERVIÇOS PARA EDIFÍCIOS E ATIVIDADES PAISAGÍSTICAS | 2 | 4 |
| COLETA, TRATAMENTO E DISPOSIÇÃO DE RESÍDUOS | 11 | 3 |
| ESGOTO E ATIVIDADES RELACIONADAS | 6 | 3 |
| FABRICAÇÃO DE PRODUTOS DIVERSOS | 4 | 3 |
| ORGANISMOS INTERNACIONAIS E OUTRAS INSTITUIÇÕES EXTRATERRITORIAIS | 2 | 3 |
| PUBLICIDADE E PESQUISA DE MERCADO | 3 | 3 |
| TRANSPORTE AÉREO | 2 | 3 |
| TRANSPORTE AQUAVIÁRIO | 3 | 3 |
| ATIVIDADES DE APOIO À EXTRAÇÃO DE MINERAIS | 2 | 2 |
| ATIVIDADES DOS SERVIÇOS DE TECNOLOGIA DA INFORMAÇÃO | 2 | 2 |
| FABRICAÇÃO DE CELULOSE, PAPEL E PRODUTOS DE PAPEL | 5 | 2 |
| FABRICAÇÃO DE EQUIPAMENTOS DE INFORMÁTICA, PRODUTOS ELETRÔNICOS E ÓPTICOS | 4 | 2 |
| FABRICAÇÃO DE PRODUTOS DO FUMO | 1 | 2 |
| SERVIÇOS DE ESCRITÓRIO, DE APOIO ADMINISTRATIVO E OUTROS SERVIÇOS PRESTADOS ÀS EMPRESAS | 4 | 2 |
| ATIVIDADES DE EXPLORAÇÃO DE JOGOS DE AZAR E APOSTAS | 5 | 1 |
| EXTRAÇÃO DE MINERAIS METÁLICOS | 1 | 1 |
| FABRICAÇÃO DE PRODUTOS FARMOQUÍMICOS E FARMACÊUTICOS | 4 | 1 |
| SELEÇÃO, AGENCIAMENTO E LOCAÇÃO DE MÃO-DE-OBRA | 3 | 1 |
| DESCONTAMINAÇÃO E OUTROS SERVIÇOS DE GESTÃO DE RESÍDUOS | 0 | 0 |
| EXTRAÇÃO DE CARVÃO MINERAL | 12 | 0 |
| EXTRAÇÃO DE PETRÓLEO E GÁS NATURAL | 1 | 0 |
Olhando os dados acima, percebemos que as divisões “Agricultura,…” e “Administração pública, …” são as mais ubíqüas, ou seja, as que mais apresentam municípios especializados nessas divisões, consideradas básicas. São em geral atividades de baixa complexidade econômica. É possível observar que mais municípios se especializaram nelas de 2006 (T0) para 2016 (T1).
Referências
BALASSA, B. Trade Liberalization and Revealed Comparative Advantage, The Manchester School 33: 99-123. 1965.
BALLAND, P.A. Economic Geography in R: Introduction to the EconGeo Package, Papers in Evolutionary Economic Geography, 17 (09): 1-75, 2017.
BALLAND, Pierre-Alexandre. EconGeo: Computing Key Indicators of the Spatial Distribution of Economic Activities. R package version 1.3. 2019. Disponível em : https://github.com/PABalland/EconGeo
COUTINHO, Márcio R. A contribuição das atividades econômicas de base agropecuária na geração de emprego e massa salarial para os municípios de Mato Grosso do Sul. Dissertação de Mestrado (Administração). Campo Grande: UFMS, 2017. p.32-42.
CRUZ, B.O.;QUEIROZ, I.V. Efeitos encadeados do perfil setorial dos investimentos e a distribuição espacial da indústria: onde se localizam as indústrias dos setores com maiores impactos? Texto para discussão n. 2172, Brasília: IPEA, p.27.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: Mapas em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019a. Disponível em: http://rpubs.com/amrofi/Regional_Economics_Spatial.
FIGUEIREDO, Adriano Marcos Rodrigues. Apêndice - instalação do RStudio. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019b. Disponível em: http://rpubs.com/amrofi/instrucoes_Rstudio.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: polos, diversidade e especialização em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019c. Disponível em: http://rpubs.com/amrofi/Regional_Economics_poles_diversity.
FIGUEIREDO, Adriano Marcos Rodrigues. Mapas em R com geobr. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020a. Disponível em: http://rpubs.com/amrofi/maps_geobr e https://adrianofigueiredo.netlify.com/post/mapas-em-r-com-geobr/.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: \(CV\), \(V_w\) e \(Theil\) em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020b. Disponível em http://rpubs.com/amrofi/regional_indicadores_1 e https://adrianofigueiredo.netlify.app/post/economia-regional-em-r-indicadores-de-analise-cv-v-w-e-theil/.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: reprodução de medidas de LQ conforme Haddad (2018) em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020c. Disponível em https://adrianofigueiredo.netlify.app/post/economia-regional-reproducao-de-medidas-de-lq/ e em http://rpubs.com/amrofi/medidas_QL_haddad_regional.
FLORENCE, P. Sargent. Investment, location, and size of plant. Cambridge: Cambridge University Press, 1948.
HOOVER, Edgar M.; GIARRATANI, Frank. An Introduction to Regional Economics, The Web Book of Regional Science. West Virginia: Regional research Institute, West Virginia University. Disponível em: <www.rri.wvu.edu/WebBook/Giarratani/chapternine.htm>, v. 9, 1984. Atualizado em: Hoover, Edgar M. and Giarratani, Frank, “An Introduction to Regional Economics” (2020). Web Book of Regional Science. 4. https://researchrepository.wvu.edu/rri-web-book/4.
IBGE - Instituto Brasileiro de Geografia e Estatística. Produto Interno Bruto dos Municípios. Rio de Janeiro: IBGE/SIDRA. 2020a. Disponível em:https://sidra.ibge.gov.br/pesquisa/pib-munic/tabelas.
IBGE - Instituto Brasileiro de Geografia e Estatística. Estimativas de população. Rio de Janeiro: IBGE/SIDRA. 2020b. Disponível em: https://www.ibge.gov.br/estatisticas/sociais/populacao/9103-estimativas-de-populacao.html?=&t=downloads
LAUTERT, V.; ARAUJO, N.C.M. Concentração industrial no Brasil no período 1996-2001: uma análise por meio do índice de Ellison e Glaeser (1994). Economia Aplicada, São Paulo, v. 11, n. 3, p. 347-368, Jul.-Set., 2007.
MONASTERIO, Leonardo. Indicadores de análise regional e espacial. In: CRUZ et al (orgs). Economia regional e urbana : teorias e métodos com ênfase no Brasil. Brasília: Ipea, 2011. cap. 10. pp.315-331.
NORTH, Douglas. Teoria da localização e crescimento econômico regional. In: SCWARTZMANN, J. (org.) Economia regional e urbana: tetos escolhidos. Belo Horizonte: UFMG, p.333-343, 1977.
Pereira et al. Quantifying Urban Centrality: A Simple Index Proposal And International Comparison. Brasília: Ipea, 2012. Disponível em: http://ipea.gov.br/agencia/images/stories/PDFs/TDs/td_1675a.pdf.
SOUZA, Filipe Lage de. A localização da indústria de transformação brasileira nas últimas três décadas. Rio de Janeiro: EPGE-FGV, 2002. (Dissertação, Mestrado em Economia). 130p.
WIELAND, T. REAT: A Regional Economic Analysis Toolbox for R. REGION, 6(3), R1-R57. 2019. Disponível em: https://doi.org/10.18335/region.v6i3.267.