Economia Regional em R: Indicadores de localização - Coeficiente de Localização, Potencial de mercado, Centro econômico, Ellison-Glaeser, Separação espacial de Venables, Proximidade, Centralidade Urbana
Licença
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.

License: CC BY-SA 4.0
Citação
Sugestão de citação: FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional em R: Indicadores de localização - Coeficiente de Localização, Potencial de mercado, Centro econômico, Ellison-Glaeser, Separação espacial de Venables, Proximidade, Centralidade Urbana. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020. Disponível em http://rpubs.com/amrofi/regional_indicators_3 e https://adrianofigueiredo.netlify.app/post/Regional_Economics_CEmaps/.
Script para reprodução (se utilizar, citar como acima)
Download 2020-05-06-economia-regional-em-r-indicadores-de-analise-3.RmdIntrodução
Este material é uma sequência ao conteúdo das duas partes anteriores disponíveis em Figueiredo (2020b;2020c). Na primeira parte foram apresentados os indicadores de desigualdade, e na segunda os de especialização. Agora falaremos dos indicadores de localização regional, conforme cita Monastério (2011), e outras leituras úteis além deste autor, são Coutinho (2017) e Hoover e Giarratani (1984;2020). Utilizaremos os pacotes REAT de Wieland (2019); e EconGeo de Balland (2017, 2019), além de algumas funções próprias.
Indicadores de Localização Regional
O objetivo desses indicadores é resumir os padrões espaciais da atividade econômica, tentando compreender como um setor está distribuído em um local ou região, ou ainda, quais os locais mais importantes para um setor. A localização refere-se a medir o quão concentrados regionalmente estão os setores. Em geral, os indicadores de localização podem ser adaptados a partir dos de especialização, com a diferença de que os indicadores deste tipo se referem aos setores econômicos e não mais às regiões.
As primeiras referências no assunto são atribuídas a Florence (1948), citado por Monastério (2011), North (1977) entre outros.
A ideia básica deste arquivo é orientar os procedimentos para o cálculo dos indicadores de análise regional a saber:
- Coeficiente de Localização (\(CL\))
- Centro econômico
- Potencial de mercado (\(MP\) no inglês, Market Potential)
- Índice de Ellison-Glaeser (\(EGI\))
- Índice de Separação Espacial (\(ISP\) - Spatial Separation Index ou de Venables \(V\))
- Índice de Centralidade Urbana \(UCI\)
Coeficiente de Localização de Florence (\(CL\))
As primeiras referências para o coeficiente de localização são atribuídas a Florence (1948), citado por Monastério (2011), North (1977) entre outros. North (1977) ainda menciona o trabalho de Hildebrand e Mace Jr. (1950) com um quociente de localização que conduz ao mesmo resultado, conforme reconhecido por North(1977, p.301). O raciocínio para este coeficiente envolve a comparação da concentração do emprego de uma atividade em um local de análise (por exemplo o município), com um local de referência (por exemplo, o estado).
A expressão básica é muito similar à do \(CE\), para setores \(k\) e localidades \(i\), mas agora somando entre localidades \(i\), conforme Monastério (2011) dada por:
\[ C{L_k} = \frac{1}{2}\sum\limits_i {\left| {\frac{{{E_{ki}}}}{{{E_k}}} - \frac{{{E_i}}}{E}} \right|} \]
em que: \({E_{ki}}\) é o emprego no setor \(k\) na localidade de análise \(i\); \({E_i}\) é o emprego total na localidade de análise \(i\); \({E_k}\) é o emprego no setor \(k\) da localidade de referência; e \(E\) é o emprego total da localidade de referência.
Organização dos dados
Para o cálculo de \(CL\), necessita-se dos dados de emprego por setor em cada município de MS. Desta forma, chama-se a planilha já preparada com os dados da base de informações RAIS do Ministério do Trabalho e Emprego do Brasil (MTE). Um meio de obter tais informações eletronicamente é pelo pacote raisr. Outra forma é pela página da Secretaria do Trabalho do Ministério da Economia (antigo Ministério do Trabalho e Emprego - MTE) http://pdet.mte.gov.br/.
A RAIS possui os dados para o final de cada ano (dezembro), portanto, os saldos de empregados ocupados. A CAGED apresenta outro tipo de informação, a de ligados e desligados, invés do saldo de pessoas ocupadas. Utilizaremos os dados da RAIS por vínculos, por Divisão CNAE 2.0 e por município. Outras agregações podem ser testadas, a critério do usuário. O procedimento recomendado é baixar os dados primeiro, organizar e depois chamar a planilha consolidada para o No site, só consegui essa extratificação para após 2006. Sugiro olhar o video ilustrativo em https://youtu.be/b93l_T3xhiA.
Criei uma função para realizar as operações conforme a fórmula de CL acima.
CL <- function(mat) {
mat <- as.matrix(mat)
share_tech_city <- t(round(t(mat)/rowSums(t(mat)), 4)) #regional shares
share_tech_total <- colSums(t(mat))/sum(t(mat)) # regional share total
CL <- abs(share_tech_city - share_tech_total)
CL[is.na(CL)] <- 0
CL <- 0.5 * colSums(CL)
return(CL)
}Utilizarei a mesma matriz básica (mat_0) para 2006 e mat_1 para 2016, como em Figueiredo (2020c).
- Para 2006:
library(readxl)
dadosemprego <- read_excel("emprego.xlsx", sheet = "2006")
mat_0 <- as.matrix(dadosemprego[1:79, 2:88]) # 2006
cl.ms_0 <- round(CL(mat_0), 4)
share_tech_city <- t(round(t(mat_0)/rowSums(t(mat_0)), 4)) #regional shares
share_tech_total <- colSums(t(mat_0))/sum(t(mat_0)) # regional share total- Para 2016:
dadosemprego_1 <- read_excel("emprego.xlsx", sheet = "2016")
mat_1 <- as.matrix(dadosemprego_1[1:79, 2:88]) # 2016
cl.ms_1 <- round(CL(mat_1), 4)
CL.MS <- cbind(cl.ms_0, cl.ms_1)
colnames(CL.MS) <- c("CL.2006", "CL.2016")
knitr::kable(CL.MS)| CL.2006 | CL.2016 | |
|---|---|---|
| ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL | 0.1660 | 0.1794 |
| AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS | 0.3380 | 0.3923 |
| AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS | 0.4511 | 0.4828 |
| ALIMENTAÇÃO | 0.1506 | 0.1350 |
| ALOJAMENTO | 0.2516 | 0.2712 |
| ALUGUÉIS NÃO-IMOBILIÁRIOS E GESTÃO DE ATIVOS INTANGÍVEIS NÃO-FINANCEIROS | 0.4010 | 0.2875 |
| ARMAZENAMENTO E ATIVIDADES AUXILIARES DOS TRANSPORTES | 0.2449 | 0.2811 |
| ATIVIDADES ARTÍSTICAS, CRIATIVAS E DE ESPETÁCULOS | 0.4534 | 0.4825 |
| ATIVIDADES AUXILIARES DOS SERVIÇOS FINANCEIROS, SEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 0.3476 | 0.3177 |
| ATIVIDADES CINEMATOGRÁFICAS, PRODUÇÃO DE VÍDEOS E DE PROGRAMAS DE TELEVISÃO | 0.3364 | 0.3975 |
| ATIVIDADES DE APOIO À EXTRAÇÃO DE MINERAIS | 0.9775 | 0.9149 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA | 0.2505 | 0.2300 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA INTEGRADAS COM ASSISTÊNCIA SOCIAL, PRESTADAS EM RESIDÊNCIAS COLETIVAS E PARTICULARES | 0.4469 | 0.3664 |
| ATIVIDADES DE EXPLORAÇÃO DE JOGOS DE AZAR E APOSTAS | 0.4712 | 0.9878 |
| ATIVIDADES DE ORGANIZAÇÕES ASSOCIATIVAS | 0.2406 | 0.3551 |
| ATIVIDADES DE PRESTAÇÃO DE SERVIÇOS DE INFORMAÇÃO | 0.2748 | 0.3192 |
| ATIVIDADES DE RÁDIO E DE TELEVISÃO | 0.1965 | 0.2255 |
| ATIVIDADES DE SEDES DE EMPRESAS E DE CONSULTORIA EM GESTÃO EMPRESARIAL | 0.4425 | 0.4182 |
| ATIVIDADES DE SERVIÇOS FINANCEIROS | 0.1501 | 0.1164 |
| ATIVIDADES DE VIGILÂNCIA, SEGURANÇA E INVESTIGAÇÃO | 0.3797 | 0.3740 |
| ATIVIDADES DOS SERVIÇOS DE TECNOLOGIA DA INFORMAÇÃO | 0.4972 | 0.5008 |
| ATIVIDADES ESPORTIVAS E DE RECREAÇÃO E LAZER | 0.2236 | 0.2164 |
| ATIVIDADES IMOBILIÁRIAS | 0.3315 | 0.2531 |
| ATIVIDADES JURÍDICAS, DE CONTABILIDADE E DE AUDITORIA | 0.1753 | 0.1067 |
| ATIVIDADES LIGADAS AO PATRIMÔNIO CULTURAL E AMBIENTAL | 0.4891 | 0.8678 |
| ATIVIDADES VETERINÁRIAS | 0.3020 | 0.3435 |
| CAPTAÇÃO, TRATAMENTO E DISTRIBUIÇÃO DE ÁGUA | 0.4884 | 0.5503 |
| COLETA, TRATAMENTO E DISPOSIÇÃO DE RESÍDUOS | 0.6902 | 0.4363 |
| COMÉRCIO E REPARAÇÃO DE VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 0.1696 | 0.1409 |
| COMÉRCIO POR ATACADO, EXCETO VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 0.1427 | 0.1687 |
| COMÉRCIO VAREJISTA | 0.1080 | 0.0795 |
| CONFECÇÃO DE ARTIGOS DO VESTUÁRIO E ACESSÓRIOS | 0.4366 | 0.2966 |
| CONSTRUÇÃO DE EDIFÍCIOS | 0.3913 | 0.2984 |
| CORREIO E OUTRAS ATIVIDADES DE ENTREGA | 0.2111 | 0.2148 |
| DESCONTAMINAÇÃO E OUTROS SERVIÇOS DE GESTÃO DE RESÍDUOS | 0.0000 | 0.0000 |
| EDIÇÃO E EDIÇÃO INTEGRADA À IMPRESSÃO | 0.3352 | 0.2676 |
| EDUCAÇÃO | 0.2314 | 0.2692 |
| ELETRICIDADE, GÁS E OUTRAS UTILIDADES | 0.2382 | 0.2116 |
| ESGOTO E ATIVIDADES RELACIONADAS | 0.4507 | 0.4603 |
| EXTRAÇÃO DE CARVÃO MINERAL | 0.7526 | 0.0000 |
| EXTRAÇÃO DE MINERAIS METÁLICOS | 0.9697 | 0.9688 |
| EXTRAÇÃO DE MINERAIS NÃO-METÁLICOS | 0.4968 | 0.6813 |
| EXTRAÇÃO DE PETRÓLEO E GÁS NATURAL | 0.5326 | 0.0000 |
| FABRICAÇÃO DE BEBIDAS | 0.4912 | 0.5150 |
| FABRICAÇÃO DE CELULOSE, PAPEL E PRODUTOS DE PAPEL | 0.4322 | 0.8597 |
| FABRICAÇÃO DE COQUE, DE PRODUTOS DERIVADOS DO PETRÓLEO E DE BIOCOMBUSTÍVEIS | 0.8706 | 0.7683 |
| FABRICAÇÃO DE EQUIPAMENTOS DE INFORMÁTICA, PRODUTOS ELETRÔNICOS E ÓPTICOS | 0.4647 | 0.5724 |
| FABRICAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 0.3333 | 0.3415 |
| FABRICAÇÃO DE MÁQUINAS, APARELHOS E MATERIAIS ELÉTRICOS | 0.6893 | 0.8210 |
| FABRICAÇÃO DE MÓVEIS | 0.3319 | 0.3712 |
| FABRICAÇÃO DE OUTROS EQUIPAMENTOS DE TRANSPORTE, EXCETO VEÍCULOS AUTOMOTORES | 0.9139 | 0.9450 |
| FABRICAÇÃO DE PRODUTOS ALIMENTÍCIOS | 0.5239 | 0.4851 |
| FABRICAÇÃO DE PRODUTOS DE BORRACHA E DE MATERIAL PLÁSTICO | 0.3880 | 0.4513 |
| FABRICAÇÃO DE PRODUTOS DE MADEIRA | 0.5301 | 0.4645 |
| FABRICAÇÃO DE PRODUTOS DE METAL, EXCETO MÁQUINAS E EQUIPAMENTOS | 0.4012 | 0.2280 |
| FABRICAÇÃO DE PRODUTOS DE MINERAIS NÃO-METÁLICOS | 0.4468 | 0.3627 |
| FABRICAÇÃO DE PRODUTOS DIVERSOS | 0.4808 | 0.5181 |
| FABRICAÇÃO DE PRODUTOS DO FUMO | 0.5326 | 0.5705 |
| FABRICAÇÃO DE PRODUTOS FARMOQUÍMICOS E FARMACÊUTICOS | 0.5162 | 0.5821 |
| FABRICAÇÃO DE PRODUTOS QUÍMICOS | 0.3645 | 0.3708 |
| FABRICAÇÃO DE PRODUTOS TÊXTEIS | 0.7975 | 0.7219 |
| FABRICAÇÃO DE VEÍCULOS AUTOMOTORES, REBOQUES E CARROCERIAS | 0.3682 | 0.3742 |
| IMPRESSÃO E REPRODUÇÃO DE GRAVAÇÕES | 0.2871 | 0.1968 |
| MANUTENÇÃO, REPARAÇÃO E INSTALAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 0.2648 | 0.3065 |
| METALURGIA | 0.7738 | 0.7680 |
| OBRAS DE INFRA-ESTRUTURA | 0.3149 | 0.3646 |
| ORGANISMOS INTERNACIONAIS E OUTRAS INSTITUIÇÕES EXTRATERRITORIAIS | 0.5133 | 0.9056 |
| OUTRAS ATIVIDADES DE SERVIÇOS PESSOAIS | 0.2280 | 0.1989 |
| OUTRAS ATIVIDADES PROFISSIONAIS, CIENTÍFICAS E TÉCNICAS | 0.2636 | 0.3550 |
| PESCA E AQÜICULTURA | 0.8121 | 0.8288 |
| PESQUISA E DESENVOLVIMENTO CIENTÍFICO | 0.4146 | 0.4382 |
| PREPARAÇÃO DE COUROS E FABRICAÇÃO DE ARTEFATOS DE COURO, ARTIGOS PARA VIAGEM E CALÇADOS | 0.5031 | 0.6367 |
| PRODUÇÃO FLORESTAL | 0.7526 | 0.7962 |
| PUBLICIDADE E PESQUISA DE MERCADO | 0.3987 | 0.4451 |
| REPARAÇÃO E MANUTENÇÃO DE EQUIPAMENTOS DE INFORMÁTICA E COMUNICAÇÃO E DE OBJETOS PESSOAIS E DOMÉSTICOS | 0.2947 | 0.2512 |
| SEGUROS, RESSEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 0.4209 | 0.4172 |
| SELEÇÃO, AGENCIAMENTO E LOCAÇÃO DE MÃO-DE-OBRA | 0.3983 | 0.5780 |
| SERVIÇOS DE ARQUITETURA E ENGENHARIA | 0.5414 | 0.3470 |
| SERVIÇOS DE ASSISTÊNCIA SOCIAL SEM ALOJAMENTO | 0.2900 | 0.3604 |
| SERVIÇOS DE ESCRITÓRIO, DE APOIO ADMINISTRATIVO E OUTROS SERVIÇOS PRESTADOS ÀS EMPRESAS | 0.3789 | 0.3809 |
| SERVIÇOS DOMÉSTICOS | 0.2128 | 0.5691 |
| SERVIÇOS ESPECIALIZADOS PARA CONSTRUÇÃO | 0.3340 | 0.2221 |
| SERVIÇOS PARA EDIFÍCIOS E ATIVIDADES PAISAGÍSTICAS | 0.4120 | 0.4192 |
| TELECOMUNICAÇÕES | 0.4051 | 0.2370 |
| TRANSPORTE AÉREO | 0.4877 | 0.4699 |
| TRANSPORTE AQUAVIÁRIO | 0.8655 | 0.9527 |
| TRANSPORTE TERRESTRE | 0.2061 | 0.1377 |
# salvar data.frames para csv com write.csv() ou para excel
writexl::write_xlsx(as.data.frame(CL.MS), "clms2006_2016.xlsx")Potencial de Mercado
Ceteris paribus e intuitivamente, um potencial de mercado elevado indica o quão atraente para as atividades econômicas uma região é. A proximidade de mercados é vantajosa para as empresas uma vez que fornecedores e consumidores estarão mais acessíveis. Obviamente, existem outras forças em jogo, mas as medidas de potencial de mercado buscam capturar exatamente tal proximidade.
Pode-se então identificar o centro econômico de uma região e calcular quão próximo se está deste centro.
Centro econômico (CEC)
O centro econômico ponderado de um país pode ser identificado encontrando as coordenadas do centro \((x_m,y_m)\), conforme:
\[ {x_m} = \sum\limits_{i = 1}^n {\left( {{x_i}\frac{{PI{B_i}}}{{\sum\limits_{i = 1}^n {PI{B_i}} }}} \right)} \] e
\[ {y_m} = \sum\limits_{i = 1}^n {\left( {{y_i}\frac{{PI{B_i}}}{{\sum\limits_{i = 1}^n {PI{B_i}} }}} \right)} \]
onde \(y_i\), \(x_i\) são latitudes e longitudes dos centroides de cada região \(i\) e \(PIB_i\) refere-se ao Produto Interno Bruto, ou outra variável econômica relevante.
Portanto, seja um dataset contendo os valores dos PIB municipais e respectivas coordenadas dos centróides. Seja o exemplo de cálculo do Potencial de Mercado conforme Monasterio (2011) (HARRIS, 1954 apud BRAKMAN, GARRETSEN e MARREWIJK, 2003, p. 35-37). O potencial de mercado de uma região é definido como:
# variaveis do dataset, a partir do shapefile do IBGE e adaptado 79 municipios de
# Mato Grosso do Sul, 2002-2015
library(readxl)
library(foreign)
load("dados.pot.Rda")
# View(dados.pot)
attach(dados.pot)
# codmun - codigo do municipio no IBGE 7 digitos nomemun - nome do municipio lat
# - latitude conforme consta no shapefile do IBGE long - longitude conforme
# consta no shapefile do IBGE pib - pib municipal em valores correntes (R$ 1000)
# SCN 2010
pib <- dados.pot[89:102]
# pop - populacao municipal estimada pelo IBGE para o TCU
pop <- dados.pot[103:116]
# pibpc - pib per capita municipal em valores correntes
pibpc <- dados.pot[117:130]
# MPi , o potencial de mercado da região i, é o somatório da demanda nos locais j
# (Mj), ponderada pela distância entre i e j (Dij).Neste exemplo faremos o uso da distância ao centro economico como a distancia para avaliacao do potencial de mercado.
# determinacao do centro economico, composto de uma latitude e longitude passo 1:
# calculo da parcela do PIB municipal no PIB estadual
attach(pib)
attach(dados.pot)
Si <- pib2015/(sum(pib2015))
xc.pib2015 <- I(long * Si)
yc.pib2015 <- I(lat * Si)
xm <- sum(xc.pib2015) # coordenada do centro economico
ym <- sum(yc.pib2015)
# coordenadas do centro economico em UTM metros
centro.economico <- c(xm, ym)
centro.economico[1] -54.26200 -20.92285# -54.26200,-20.92285O resultado gráfico pode ser plotado no Google Maps ou Google Earth como abaixo:
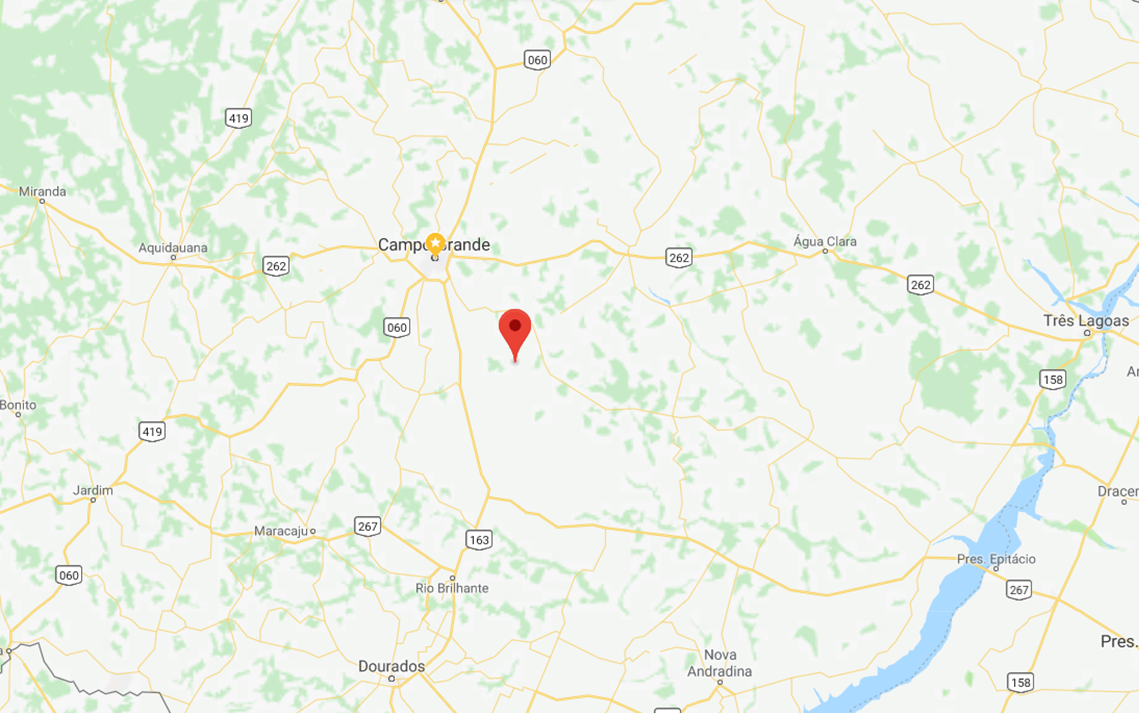
Plotagem do centro econômico de MS em 2015
Distancia do municipio ao centro economico (D)
Uma vez estimado o centro econômico, é calculada a distância entre este e os centros das outras regiões. Para o cálculo da distância euclidiana da região i(disti) ao centro econômico, basta calcular:
\[ dis{t_i} = \sqrt {{{({x_i} - {x_m})}^2} + {{({y_i} - {y_m})}^2}} \]
Segue o código em R, utilizando o pacote geosphere e a função distGeo:
attach(pib)
attach(dados.pot)
# distancia do municipio ao centro economico
# dist.ce<-sqrt((long-xm)^2+(lat-ym)^2) dist.ce
library(geosphere)
attach(dados.pot)
# calculo individual para Agua Clara
dist.ce <- distGeo(c(-52.878, -20.448), c(-54.262, -20.92285))
# distancia em metros
dist.ce[1] 153478.1# distancia em km
dist.ce/1000[1] 153.4781# Calculo para todos os municipios
dist.teste <- cbind(long, lat)
dist.ce.all <- distGeo(dist.teste, c(-54.262, -20.92285))
dist.km.all <- dist.ce.all/1000
dados.full <- cbind(dados.pot, Si, xc.pib2015, yc.pib2015, dist.km.all)Potencial de mercado para com o centro econômico (PM)
# potencial de mercado para com o centro economico Dij = dist.km.all MPi =
# soma(Mj/Dij) para Mj = pib*1000
MPmun2015 <- pib2015 * 1000/dist.km.all
MP.CE <- sum(MPmun2015) #RETIRAR DA SOMA O MUNICIPIO DE REFERENCIA!
MP.CE[1] 697138467dados.full <- cbind(pib, Si, xc.pib2015, yc.pib2015, dist.km.all, MPmun2015)
tabela <- cbind(nomemun, MPmun2015)
writexl::write_xlsx(as.data.frame(dados.full), "dadospot.xlsx")Índice de localização de Ellison-Glaeser (EGI)
O Índice de localização de Ellison-Glaeser (\(EGI_k\)) para um setor \(k\) entre os municípios \(i\) é uma sugestão de Ellison e Glaeser (1997) como forma de correcçao dos indicadores clássicos tipo coeficiente de localização de Florence ou Hoover, ou Gini. Conforme Feser (2000), uma diferença importante é que ele deriva de uma teoria explícita do comportamento da localização da firma.
O índice considera a concentração como a aglomeração acima do que se observaria se as firmas se localizassem de modo aleatório. Pelo argumento destes autores, o \(EGI_k\) seria robusto às diferenças no nível de agregação espacial, controlando as diferenças da distribuição dos estabelecimentos entre diferentes setores, e portanto considera o fato de que a concentração espacial em parte deriva da concentração setorial. Isto facilitaria a comparação setorial entre países distintos, por exemplo.
A expressão do índice é:
\[ EGI_k = \frac{{G - \left( {1 - \sum\limits_i {x_i^2} } \right)H}}{{\left( {1 - \sum\limits_i {x_i^2} } \right)\left( {1 - H} \right)}} \]
Para o índice de concentração de Herfindahl \(H\)
\[ H = {\sum\limits_{i = 1}^M {\left( {\frac{{{E_{ki}}}}{E}} \right)} ^2} \] ou seja, \(H\) é o somatório do volume de empregos do setor \(k\) na região \(i\) (\(E_ki\)), em razão do volume de empregos total (\(E\)) e,
\[ G = {\sum\limits_{i = 1} {\left( {\frac{{{E_{ki}}}}{{{E_k}}} - \frac{{{E_i}}}{E}} \right)} ^2} \] em que \(G\) é o somatório do quadrado da diferença entre a parcela do emprego do setor \(k\) na região \(i\) volume de empregos do setor \(k\) na região \(i\) (\(E_{ki}/E_k\)), e a parcela do emprego industrial na área (\(x_i = E_i /E\)).
O índice de Ellison-Glaeser, portanto, considera a concentração setorial \(H\) em sua fórmula, em que \(0\le H\le1\). Menores valores de \(EGI_k\) indicam fraca localização, por exemplo entre 0 e 0,02, e valores de \(EGI_k\) maiores que 0,05 indicam intensa localização (Monastério, 2011). Existe o risco de uma má interpretação, por exemplo, imaginando se ter concentração espacial
library(readxl)
dadosemprego <- read_excel("emprego.xlsx", sheet = "2006")
# View(dadosemprego) attach(dadosemprego)
# ei<-rowSums(as.matrix(dadosemprego[,2:88]))
E <- colSums(dadosemprego[, 89], dims = 1)
ei <- dadosemprego[, 89]
# ei é o emprego total da regiao i, E é o emprego total MS Ek é o emprego total
# MS do setor k
Ek <- t(colSums(dadosemprego[, 2:88], dims = 1))
# função EGI
EGI <- function(eki, ei, Ek, E) {
s_ki <- eki/Ek
s_i <- ei/E
G <- sum((s_ki - s_i)^2)
H <- sum((eki/E)^2)
Z <- 1 - sum((s_i^2))
EGk <- ((G - Z * H)/(Z * (1 - H)))
return(EGk)
}
# teste - divisao 2
EGI.div <- EGI(dadosemprego$`AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS`,
ei, Ek[1, 2], E)
EGI.div[1] 0.04959096Portanto, um indicador \(EGI=0.04959\) indica uma média para intensa localização segundo Ellison-Glaeser. Pode-se generalizar a função para todos os setores \(k\), automatizar para todas as colunas e ano de 2006:
require(knitr)
# EGI <- function (eki, ei, Ek, E) retirar zeros de paraiso das aguas
dados2 <- dadosemprego[-c(58), ]
# View(dados2)
ei <- dados2$`Total Geral`
E <- colSums(dados2[, 89], dims = 1)
Ek <- t(colSums(dados2[, 2:88], dims = 1))
setores <- names(dados2[, 2:88])
# inicializar EGI
EGI.MS.2006 <- 0
for (k in 1:87) {
dadosemp2 <- dados2[1:78, k + 1]
EGI.2006 <- EGI(dadosemp2, ei, Ek[1, k], E)
EGI.MS.2006[k] <- EGI.2006
}
EGI.MS.2006 <- cbind((names(dados2[, 2:88])), round(EGI.MS.2006, 4))
writexl::write_xlsx(as.data.frame(EGI.MS.2006), "EGIMS2006.xls")
knitr::kable(EGI.MS.2006)| ADMINISTRAÇÃO PÚBLICA, DEFESA E SEGURIDADE SOCIAL | -0.0033 |
| AGÊNCIAS DE VIAGENS, OPERADORES TURÍSTICOS E SERVIÇOS DE RESERVAS | 0.0496 |
| AGRICULTURA, PECUÁRIA E SERVIÇOS RELACIONADOS | 0.2103 |
| ALIMENTAÇÃO | 0.0066 |
| ALOJAMENTO | 0.0324 |
| ALUGUÉIS NÃO-IMOBILIÁRIOS E GESTÃO DE ATIVOS INTANGÍVEIS NÃO-FINANCEIROS | 0.1988 |
| ARMAZENAMENTO E ATIVIDADES AUXILIARES DOS TRANSPORTES | 0.0143 |
| ATIVIDADES ARTÍSTICAS, CRIATIVAS E DE ESPETÁCULOS | 0.2258 |
| ATIVIDADES AUXILIARES DOS SERVIÇOS FINANCEIROS, SEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 0.0866 |
| ATIVIDADES CINEMATOGRÁFICAS, PRODUÇÃO DE VÍDEOS E DE PROGRAMAS DE TELEVISÃO | 0.0552 |
| ATIVIDADES DE APOIO À EXTRAÇÃO DE MINERAIS | 0.9479 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA | 0.0724 |
| ATIVIDADES DE ATENÇÃO À SAÚDE HUMANA INTEGRADAS COM ASSISTÊNCIA SOCIAL, PRESTADAS EM RESIDÊNCIAS COLETIVAS E PARTICULARES | 0.0697 |
| ATIVIDADES DE EXPLORAÇÃO DE JOGOS DE AZAR E APOSTAS | 0.2726 |
| ATIVIDADES DE ORGANIZAÇÕES ASSOCIATIVAS | 0.0446 |
| ATIVIDADES DE PRESTAÇÃO DE SERVIÇOS DE INFORMAÇÃO | 0.0372 |
| ATIVIDADES DE RÁDIO E DE TELEVISÃO | 0.0069 |
| ATIVIDADES DE SEDES DE EMPRESAS E DE CONSULTORIA EM GESTÃO EMPRESARIAL | 0.1763 |
| ATIVIDADES DE SERVIÇOS FINANCEIROS | 0.0064 |
| ATIVIDADES DE VIGILÂNCIA, SEGURANÇA E INVESTIGAÇÃO | 0.186 |
| ATIVIDADES DOS SERVIÇOS DE TECNOLOGIA DA INFORMAÇÃO | 0.3322 |
| ATIVIDADES ESPORTIVAS E DE RECREAÇÃO E LAZER | 0.0239 |
| ATIVIDADES IMOBILIÁRIAS | 0.0636 |
| ATIVIDADES JURÍDICAS, DE CONTABILIDADE E DE AUDITORIA | 0.0142 |
| ATIVIDADES LIGADAS AO PATRIMÔNIO CULTURAL E AMBIENTAL | 0.1199 |
| ATIVIDADES VETERINÁRIAS | 0.0348 |
| CAPTAÇÃO, TRATAMENTO E DISTRIBUIÇÃO DE ÁGUA | 0.2536 |
| COLETA, TRATAMENTO E DISPOSIÇÃO DE RESÍDUOS | 0.2728 |
| COMÉRCIO E REPARAÇÃO DE VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 0.0105 |
| COMÉRCIO POR ATACADO, EXCETO VEÍCULOS AUTOMOTORES E MOTOCICLETAS | 0.0056 |
| COMÉRCIO VAREJISTA | 7e-04 |
| CONFECÇÃO DE ARTIGOS DO VESTUÁRIO E ACESSÓRIOS | 0.0774 |
| CONSTRUÇÃO DE EDIFÍCIOS | 0.2032 |
| CORREIO E OUTRAS ATIVIDADES DE ENTREGA | 0.0538 |
| DESCONTAMINAÇÃO E OUTROS SERVIÇOS DE GESTÃO DE RESÍDUOS | NaN |
| EDIÇÃO E EDIÇÃO INTEGRADA À IMPRESSÃO | 0.0939 |
| EDUCAÇÃO | 0.026 |
| ELETRICIDADE, GÁS E OUTRAS UTILIDADES | 0.026 |
| ESGOTO E ATIVIDADES RELACIONADAS | 0.1079 |
| EXTRAÇÃO DE CARVÃO MINERAL | 0.2224 |
| EXTRAÇÃO DE MINERAIS METÁLICOS | 1.5207 |
| EXTRAÇÃO DE MINERAIS NÃO-METÁLICOS | 0.1048 |
| EXTRAÇÃO DE PETRÓLEO E GÁS NATURAL | 0.3843 |
| FABRICAÇÃO DE BEBIDAS | 0.2497 |
| FABRICAÇÃO DE CELULOSE, PAPEL E PRODUTOS DE PAPEL | 0.1151 |
| FABRICAÇÃO DE COQUE, DE PRODUTOS DERIVADOS DO PETRÓLEO E DE BIOCOMBUSTÍVEIS | 0.4541 |
| FABRICAÇÃO DE EQUIPAMENTOS DE INFORMÁTICA, PRODUTOS ELETRÔNICOS E ÓPTICOS | 0.0883 |
| FABRICAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 0.0554 |
| FABRICAÇÃO DE MÁQUINAS, APARELHOS E MATERIAIS ELÉTRICOS | 0.5181 |
| FABRICAÇÃO DE MÓVEIS | 0.0404 |
| FABRICAÇÃO DE OUTROS EQUIPAMENTOS DE TRANSPORTE, EXCETO VEÍCULOS AUTOMOTORES | 0.7756 |
| FABRICAÇÃO DE PRODUTOS ALIMENTÍCIOS | 0.1953 |
| FABRICAÇÃO DE PRODUTOS DE BORRACHA E DE MATERIAL PLÁSTICO | 0.1159 |
| FABRICAÇÃO DE PRODUTOS DE MADEIRA | 0.1897 |
| FABRICAÇÃO DE PRODUTOS DE METAL, EXCETO MÁQUINAS E EQUIPAMENTOS | 0.109 |
| FABRICAÇÃO DE PRODUTOS DE MINERAIS NÃO-METÁLICOS | 0.11 |
| FABRICAÇÃO DE PRODUTOS DIVERSOS | 0.1827 |
| FABRICAÇÃO DE PRODUTOS DO FUMO | 0.3843 |
| FABRICAÇÃO DE PRODUTOS FARMOQUÍMICOS E FARMACÊUTICOS | 0.1756 |
| FABRICAÇÃO DE PRODUTOS QUÍMICOS | 0.0604 |
| FABRICAÇÃO DE PRODUTOS TÊXTEIS | 0.783 |
| FABRICAÇÃO DE VEÍCULOS AUTOMOTORES, REBOQUES E CARROCERIAS | 0.0621 |
| IMPRESSÃO E REPRODUÇÃO DE GRAVAÇÕES | 0.0487 |
| MANUTENÇÃO, REPARAÇÃO E INSTALAÇÃO DE MÁQUINAS E EQUIPAMENTOS | 0.0221 |
| METALURGIA | 0.4142 |
| OBRAS DE INFRA-ESTRUTURA | 0.0556 |
| ORGANISMOS INTERNACIONAIS E OUTRAS INSTITUIÇÕES EXTRATERRITORIAIS | 0.1882 |
| OUTRAS ATIVIDADES DE SERVIÇOS PESSOAIS | 0.0505 |
| OUTRAS ATIVIDADES PROFISSIONAIS, CIENTÍFICAS E TÉCNICAS | 0.0271 |
| PESCA E AQÜICULTURA | 0.5829 |
| PESQUISA E DESENVOLVIMENTO CIENTÍFICO | 0.0841 |
| PREPARAÇÃO DE COUROS E FABRICAÇÃO DE ARTEFATOS DE COURO, ARTIGOS PARA VIAGEM E CALÇADOS | 0.1413 |
| PRODUÇÃO FLORESTAL | 0.4949 |
| PUBLICIDADE E PESQUISA DE MERCADO | 0.1765 |
| REPARAÇÃO E MANUTENÇÃO DE EQUIPAMENTOS DE INFORMÁTICA E COMUNICAÇÃO E DE OBJETOS PESSOAIS E DOMÉSTICOS | 0.0622 |
| SEGUROS, RESSEGUROS, PREVIDÊNCIA COMPLEMENTAR E PLANOS DE SAÚDE | 0.2088 |
| SELEÇÃO, AGENCIAMENTO E LOCAÇÃO DE MÃO-DE-OBRA | 0.1665 |
| SERVIÇOS DE ARQUITETURA E ENGENHARIA | 0.3921 |
| SERVIÇOS DE ASSISTÊNCIA SOCIAL SEM ALOJAMENTO | 0.0617 |
| SERVIÇOS DE ESCRITÓRIO, DE APOIO ADMINISTRATIVO E OUTROS SERVIÇOS PRESTADOS ÀS EMPRESAS | 0.1735 |
| SERVIÇOS DOMÉSTICOS | 0.0082 |
| SERVIÇOS ESPECIALIZADOS PARA CONSTRUÇÃO | 0.0834 |
| SERVIÇOS PARA EDIFÍCIOS E ATIVIDADES PAISAGÍSTICAS | 0.2259 |
| TELECOMUNICAÇÕES | 0.1714 |
| TRANSPORTE AÉREO | 0.2803 |
| TRANSPORTE AQUAVIÁRIO | 0.8101 |
| TRANSPORTE TERRESTRE | 0.0176 |
Índice de separação espacial ou de Venables (V)
O Índice de Separação Espacial (\(ISP\)) ou também chamado índice de Venables (\(V\)) surge para considerar as distâncias entre as localidades em que se situam certas atividades econômicas. O coeficiente de localização (\(CL\)) não se altera quando localidades têm concentração industrial mas etão mais (ou menos) distantes enre si. Desta forma, Middelfart-Knarvik et al (2002) propuseram o \(ISP\) como:
\[ ISP_k=\sum_i \sum_j {s_{ik} s_{jk} \delta_{ij}} \] em que \(i\) e \(j\) são as localidades do setor \(k\) e \(\delta_{ij}\) é a distância entre \(i\) e \(j\). Em termos matriciais, pode-se reescrever a expressão da forma:
\[ ISP = V = S' D S \]
em que \(S_k\) é o vetor da participação do setor \(k\) nas localidades e \(D\) a matriz de distâncias.
O ISP é, portanto, como uma ‘média’ ponderada das distâncias entre municípios onde se localizam os empregos da força de trabalho nos respectivos pares de localidades. Seu intervalo de variação é dado pela distância observada entre os pares de regiões. Quanto menor o valor do ISP, mais concentrada espacialmente está o setor. O \(ISP_k\) assume valor zero para concentração perfeita em uma só localidade, e aumenta quanto mais distantes estiverem.
Sousa (2002) calculou o ISP para diversos ramos da indústria brasileira, em nível estadual, entre 1970 e 1997. Seus resultados sugerem, em linhas gerais, um incremento da separação da indústria de transformação ao longo do período.
Índice de centralidade urbana (UCI)
O código para calcular a centralidade urbana contém um dispositivo para abrir um pop-up de modo que o leitor escolha o arquivo shape a ser utilizado. Desta forma, o RMarkdown não consegue abrir automaticamente o shape sem a intervenção humana.
Estaremos corrigindo esta modalidade de modo a fazer o cálculo automático, especificando fora de uci.R o file_name, o qual indica o shapefile a ser utilizado, onde estão os dados de emprego por setores e localidades.
Dentro do uci.R, a linha que chamava para escolha do shapefile foi “#comentada”.
# Indice de Centralidade Urbana (UCI) este índice utiliza três indicadores para
# seu cálculo (V, P, e CL) P = proximidade V = Venables CL = coeficiente de
# localização de Florence (1948) utilizaremos a rotina de Pereira et al (2012)
# trabalharemos com shape para obter os centroides e as distancias
library(foreign)
library(fields)
library(sp)
library(rgeos)
library(maptools)
options(digits = 5)
# coloque os shapefiles no mesmo diretorio do projeto utilizaremos os shape de
# nome 'AED_MS79_emprego16' função UCI será armazenada à parte
file_name <<- "~/disciplinas/economia regional/laboratorio R/indicadores_3/AED_MS79_emprego16.shp"
source("~/disciplinas/economia regional/laboratorio R/indicadores_3/uci.R")
# run UCI uci(variavel) é importante conhecer os nomes da variáveis (setores)
# dentro do shape
library(spdep)
library(rgdal)
library(ctv)
library(maptools)
# MS79 <- getinfo.shape('AED_MS79_emprego16') # abrir shape MS 79 municipios sids
# <- readOGR('.', 'AED_MS79_emprego16') names(sids) agora que conheço os nomes,
# farei para 'ADMIN_CIAL'
uci(ADMIN_CIAL)
[1] "var_x"
V1
Min. : 3
1st Qu.: 328
Median : 506
Mean : 1559
3rd Qu.: 770
Max. :65781
[1] "var_x_norm"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00002 0.00267 0.00411 0.01266 0.00625 0.53405
[1] "area"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0246 0.1425 0.2603 0.3912 0.4282 5.5657
[1] "distance"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0884 1.5666 2.5948 2.8556 3.6725 6.3556
shapefile
[1,] "C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp"
v v_max mono
[1,] "1.75173588779973" "3.21972440217403" "0.455936077442864"
cl uci_max
[1,] "0.589531822841332" "0.268788826834018"resultados <- read.csv(file = "output2.csv")
print(resultados) shapefile
1 C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp
v v_max mono cl uci_max
1 1.7517 3.2197 0.45594 0.58953 0.26879# agora para CONST_CIOS
uci(CONST_CIOS)
[1] "var_x"
V1
Min. : 0
1st Qu.: 0
Median : 4
Mean : 128
3rd Qu.: 20
Max. :6244
[1] "var_x_norm"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00000 0.00000 0.00039 0.01266 0.00197 0.61554
[1] "area"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0246 0.1425 0.2603 0.3912 0.4282 5.5657
[1] "distance"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0884 1.5666 2.5948 2.8556 3.6725 6.3556
shapefile
[1,] "C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp"
v v_max mono
[1,] "1.479056624768" "3.21972440217403" "0.540626326970932"
cl uci_max
[1,] "0.831680759094358" "0.449628514001579"resultados <- read.csv(file = "output2.csv")
print(resultados) shapefile
1 C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp
v v_max mono cl uci_max
1 1.4791 3.2197 0.54063 0.83168 0.44963# comercio varejista COMRC_ISTA
uci(COMRC_ISTA)
[1] "var_x"
V1
Min. : 16
1st Qu.: 124
Median : 294
Mean : 1147
3rd Qu.: 812
Max. :37253
[1] "var_x_norm"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00018 0.00137 0.00324 0.01266 0.00896 0.41101
[1] "area"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0246 0.1425 0.2603 0.3912 0.4282 5.5657
[1] "distance"
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0884 1.5666 2.5948 2.8556 3.6725 6.3556
shapefile
[1,] "C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp"
v v_max mono
[1,] "1.89736860260646" "3.21972440217403" "0.410704654930926"
cl uci_max
[1,] "0.596047121376705" "0.244799327307591"resultados <- read.csv(file = "output2.csv")
print(resultados) shapefile
1 C:\\Users\\amrof\\Documents\\blogdown\\content\\post\\AED_MS79_emprego16.shp
v v_max mono cl uci_max
1 1.8974 3.2197 0.4107 0.59605 0.2448# apos rodar o uci uma vez, vc pode armazenar os dados de coordenadas
writexl::write_xlsx(as.data.frame(data_map), "datamap.xls")Referências
BALASSA, B. Trade Liberalization and Revealed Comparative Advantage, The Manchester School 33: 99-123. 1965.
BALLAND, P.A. Economic Geography in R: Introduction to the EconGeo Package, Papers in Evolutionary Economic Geography, 17 (09): 1-75, 2017.
BALLAND, Pierre-Alexandre. EconGeo: Computing Key Indicators of the Spatial Distribution of Economic Activities. R package version 1.3. 2019. Disponível em : https://github.com/PABalland/EconGeo
COUTINHO, Márcio R. A contribuição das atividades econômicas de base agropecuária na geração de emprego e massa salarial para os municípios de Mato Grosso do Sul. Dissertação de Mestrado (Administração). Campo Grande: UFMS, 2017. p.32-42.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: Mapas em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019a. Disponível em: http://rpubs.com/amrofi/Regional_Economics_Spatial.
FIGUEIREDO, Adriano Marcos Rodrigues. Apêndice - instalação do RStudio. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019b. Disponível em: http://rpubs.com/amrofi/instrucoes_Rstudio.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: polos, diversidade e especialização em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2019c. Disponível em: http://rpubs.com/amrofi/Regional_Economics_poles_diversity.
FIGUEIREDO, Adriano Marcos Rodrigues. Mapas em R com geobr. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020a. Disponível em: http://rpubs.com/amrofi/maps_geobr e https://adrianofigueiredo.netlify.com/post/mapas-em-r-com-geobr/.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional: \(CV\), \(V_w\) e \(Theil\) em R. Campo Grande-MS,Brasil: RStudio/Rpubs, 2020b. Disponível em http://rpubs.com/amrofi/regional_indicadores_1 e https://adrianofigueiredo.netlify.app/post/economia-regional-em-r-indicadores-de-analise-cv-v-w-e-theil/.
FIGUEIREDO, Adriano Marcos Rodrigues. Economia Regional em R: Indicadores de análise de especialização regional - \(QL\), \(CE\), \(KSI\), \(RDI\), \(DIV\), \(UBIQ\). Campo Grande-MS,Brasil: RStudio/Rpubs, 2020c. Disponível em http://rpubs.com/amrofi/regional_indicadores_2 e https://adrianofigueiredo.netlify.app/post/economia-regional-em-r-indicadores-de-analise-2/.
FLORENCE, P. Sargent. Investment, location, and size of plant. Cambridge: Cambridge University Press, 1948.
HOOVER, Edgar M.; GIARRATANI, Frank. An Introduction to Regional Economics, The Web Book of Regional Science. West Virginia: Regional research Institute, West Virginia University. Disponível em: <www.rri.wvu.edu/WebBook/Giarratani/chapternine.htm>, v. 9, 1984. Atualizado em: Hoover, Edgar M. and Giarratani, Frank, “An Introduction to Regional Economics” (2020). Web Book of Regional Science. 4. https://researchrepository.wvu.edu/rri-web-book/4.
LAUTERT, V.; ARAUJO, N.C.M. Concentração industrial no Brasil no período 1996-2001: uma análise por meio do índice de Ellison e Glaeser (1994). Economia Aplicada, São Paulo, v. 11, n. 3, p. 347-368, Jul.-Set., 2007.
MIDELFART-KNARVIK, K. H.; OVERMAN, H. G.; REDDING, S.; VENABLES, A. J. Integration and Industrial. Revue Économique, v. 53, n. 3, p. 469-481, 2002. Disponível em: https://www.cairn.info/revue-economique-2002-3-page-469.htm#
MONASTERIO, Leonardo. Indicadores de análise regional e espacial. In: CRUZ et al (orgs). Economia regional e urbana : teorias e métodos com ênfase no Brasil. Brasília: Ipea, 2011. cap. 10. pp.315-331.
NORTH, Douglas. Teoria da localização e crescimento econômico regional. In: SCWARTZMANN, J. (org.) Economia regional e urbana: tetos escolhidos. Belo Horizonte: UFMG, p.333-343, 1977.
PEREIRA et al. Quantifying Urban Centrality: A Simple Index Proposal And International Comparison. Brasília: Ipea, 2012. Disponível em: http://ipea.gov.br/agencia/images/stories/PDFs/TDs/td_1675a.pdf.
SOUZA, Filipe Lage de. A localização da indústria de transformação brasileira nas últimas três décadas. Rio de Janeiro: EPGE-FGV, 2002. (Dissertação, Mestrado em Economia). 130p.
WIELAND, T. REAT: A Regional Economic Analysis Toolbox for R. REGION, 6(3), R1-R57. 2019. Disponível em: https://doi.org/10.18335/region.v6i3.267.